Laplace แปลงตัวอย่าง ลาปลาซ แปลงร่าง. ในการแก้สมการอนุพันธ์เชิงเส้น เราจะใช้การแปลงลาปลาซ ตัวอย่างการคำนวณการแปลง Laplace
ในการแก้สมการอนุพันธ์เชิงเส้น เราจะใช้การแปลงลาปลาซ
ลาปลาซ ทรานส์ฟอร์มเรียกอัตราส่วน
การกำหนดฟังก์ชั่น x (ท)ตัวแปรที่แท้จริง NSฟังก์ชั่นจับคู่ X (s)ตัวแปรที่ซับซ้อน s (s = σ+ jω).โดยที่ x (ท)เรียกว่า ต้นฉบับ X (s)- ภาพหรือ Laplace ภาพและ NS- ตัวแปรการแปลงลาปลาซต้นฉบับจะแสดงด้วยตัวพิมพ์เล็ก และรูปภาพจะใช้อักษรตัวพิมพ์ใหญ่ในชื่อเดียวกัน
สันนิษฐานว่าฟังก์ชัน NS(NS) ขึ้นอยู่กับการแปลง Laplace มีคุณสมบัติดังต่อไปนี้:
1) ฟังก์ชั่น x (ท)ถูกกำหนดและหาอนุพันธ์ทีละส่วนได้เป็นช่วงๆ ขอบเขตล่างที่แน่นอน s0 ของตัวเลขทั้งหมด s, α0 = infs ซึ่งมีความไม่เท่าเทียมกัน (1) เรียกว่า อัตราการเติบโตของฟังก์ชัน f (t) ความคิดเห็น ในกรณีทั่วไป ความเหลื่อมล้ำจะไม่คงอยู่ แต่การประมาณนั้นใช้ได้เมื่อ e> 0 เป็นใดๆ ดังนั้น ฟังก์ชันจึงมีเลขชี้กำลังของการเติบโต в0 = สำหรับมัน ความไม่เท่าเทียมกัน \ t \ ^ M V * ^ 0 ไม่ถือ แต่ความไม่เท่าเทียมกัน | f | ^ เมย์. เงื่อนไข (1) มีข้อ จำกัด น้อยกว่าเงื่อนไข (*) มาก ตัวอย่างที่ 1 ฟังก์ชันไม่ตรงตามเงื่อนไข (") แต่เงื่อนไข (1) เป็นไปตามเงื่อนไข s> I และ A /> I ใดๆ อัตราการเติบโต 5o = นี่คือฟังก์ชันดั้งเดิม ในทางกลับกัน ฟังก์ชันนี้ไม่ใช่ฟังก์ชันดั้งเดิม แต่มีลำดับการเติบโตที่ไม่สิ้นสุด "o = + oo ฟังก์ชันดั้งเดิมที่ง่ายที่สุดคือสิ่งที่เรียกว่าฟังก์ชัน unit หากบางฟังก์ชันเป็นไปตามเงื่อนไข 1 และ 3 ของคำจำกัดความ 1 แต่ไม่เป็นไปตามเงื่อนไข 2 แสดงว่าผลิตภัณฑ์นั้นเป็นฟังก์ชันดั้งเดิมอยู่แล้ว เพื่อความง่ายของสัญกรณ์ ตามกฎแล้ว เราจะละเว้นปัจจัย rj (t) โดยตกลงว่าฟังก์ชันทั้งหมดที่เราจะพิจารณามีค่าเท่ากับศูนย์สำหรับค่าลบ t ดังนั้นหากเรากำลังพูดถึงฟังก์ชันบางอย่าง f (t) ตัวอย่างเช่น o sin ty cos t, el เป็นต้น ดังนั้นฟังก์ชันต่อไปนี้จะมีความหมายโดยนัยเสมอ (รูปที่ 2): n = n (0 รูปที่ 1 คำจำกัดความ 2 ให้ f (t) เป็นฟังก์ชันดั้งเดิม รูปภาพ ของฟังก์ชัน f (t ) โดย Laplace คือฟังก์ชัน F (p) ของตัวแปรเชิงซ้อนที่กำหนดโดยสูตร LAPLACE TRANSFORM คำจำกัดความพื้นฐาน Properties Convolution of functions การคูณ ทฤษฎีบท การหาต้นฉบับจากภาพ การใช้ทฤษฎีบทผกผันสำหรับแคลคูลัสเชิงปฏิบัติการ สูตรของ Duhamel Integration ของระบบสมการเชิงอนุพันธ์เชิงเส้นที่มีสัมประสิทธิ์คงที่ แก้สมการปริพันธ์ โดยที่อินทิกรัลถูกแทนที่ค่าบวกของกึ่งแกน t ฟังก์ชัน F (p) เรียกอีกอย่างว่าการแปลงลาปลาซของฟังก์ชัน f (f) เคอร์เนลของ การแปลง K (t) p) = e ~ pt. ความจริงที่ว่าฟังก์ชั่นมีภาพ F (p) เราจะเขียนตัวอย่างที่ 2 ค้นหาภาพ ฟังก์ชันหน่วย ร) (ท). ฟังก์ชันนี้เป็นฟังก์ชันดั้งเดิมที่มีอัตราการเติบโต 0 - 0 โดยอาศัยสูตร (2) ภาพของฟังก์ชัน rj (t) จะเป็นฟังก์ชัน หากเป็นเช่นนั้น ปริพันธ์ทางด้านขวามือของฟังก์ชัน ความเท่าเทียมกันสุดท้ายจะมาบรรจบกัน และเราจะได้รับเพื่อให้ภาพของฟังก์ชัน rj (t) จะเป็นฟังก์ชัน £ ตามที่เราตกลงกัน เราจะเขียนว่า rj (t) = 1 จากนั้นผลลัพธ์ที่ได้จะถูกเขียนดังนี้: ทฤษฎีบท 1 สำหรับฟังก์ชันดั้งเดิม f (t) ที่มีเลขชี้กำลังการเติบโต z0 ภาพ F (p) จะถูกกำหนด ในครึ่งระนาบ R ep = s > s0 และเป็นฟังก์ชันวิเคราะห์ในครึ่งระนาบนี้ (รูปที่ 3) ให้ เพื่อพิสูจน์การมีอยู่ของภาพ F (p) ในระนาบครึ่งที่ระบุ ก็เพียงพอแล้วที่จะพิสูจน์ว่าอินทิกรัลที่ไม่เหมาะสม (2) มาบรรจบกันโดยสิ้นเชิงสำหรับ a> การใช้ (3) เราได้รับซึ่งพิสูจน์การบรรจบกันแบบสัมบูรณ์ของ อินทิกรัล (2). ในเวลาเดียวกัน เราได้รับค่าประมาณของการแปลงลาปลาซ F (p) ในครึ่งระนาบของการบรรจบกันของนิพจน์การสร้างความแตกต่าง (2) อย่างเป็นทางการภายใต้เครื่องหมายปริพันธ์เทียบกับ p เราพบว่าการมีอยู่ของปริพันธ์ (5) คือ จัดตั้งขึ้นในลักษณะเดียวกับการมีอยู่ของปริพันธ์ (2) ถูกจัดตั้งขึ้น การใช้การรวมโดยส่วนต่างๆ สำหรับ F "(p) เราได้รับค่าประมาณซึ่งหมายถึงการบรรจบกันแบบสัมบูรณ์ของอินทิกรัล (5) (ระยะที่ไม่ใช่อินทิกรัล, 0., - มีขีดจำกัดศูนย์สำหรับ t + oo) อินทิกรัล ( 5) บรรจบกันอย่างสม่ำเสมอด้วยความเคารพ p เนื่องจากมันถูกทำให้เป็นสำคัญโดยอินทิกรัลบรรจบกันที่เป็นอิสระจาก p ดังนั้นความแตกต่างที่เกี่ยวกับ p นั้นถูกกฎหมายและความเท่าเทียมกัน (5) นั้นถูกต้อง เนื่องจากอนุพันธ์ F "(p) มีอยู่ Laplace เปลี่ยน F (p) ทุกที่ในครึ่งระนาบ Rep = 5> 5о เป็นฟังก์ชันการวิเคราะห์ ความไม่เท่าเทียมกัน (4) หมายถึงข้อพิสูจน์ ถ้า p แบบบางมีแนวโน้มเป็นอนันต์เพื่อให้ Re p = s เพิ่มขึ้นอย่างไม่มีกำหนด ตัวอย่างที่ 3 ให้เราหาภาพของฟังก์ชันจำนวนเชิงซ้อนใดๆ ก็ตาม เลขชี้กำลังของฟังก์ชัน / (() เท่ากับ a. > a แต่ก็เหมือนกันทุกจุด p ยกเว้นจุด p = a โดยที่ภาพนี้มีขั้วธรรมดา ในอนาคต เราจะเจอแบบเดียวกันซ้ำแล้วซ้ำเล่า สถานการณ์เมื่อภาพ F (p) เป็นฟังก์ชันวิเคราะห์ในระนาบทั้งหมดของตัวแปรเชิงซ้อน p เพราะไม่มีข้อขัดแย้งกับทฤษฎีบท 1 อันหลังยืนยันว่าในตัวแทนครึ่งระนาบ> «o ฟังก์ชัน F (p ) ไม่มีจุดเอกพจน์: พวกเขาทั้งหมดกลายเป็นโกหกทางด้านซ้ายของบรรทัด Rep = ดังนั้น หรือในบรรทัดนี้เอง แจ้งให้ทราบไม่ได้ ในแคลคูลัสปฏิบัติการ บางครั้งใช้อิมเมจเฮฟไวไซด์ของฟังก์ชัน f (f) ซึ่งกำหนดโดยความเท่าเทียมกันและแตกต่างจากอิมเมจ Laplace ด้วยปัจจัย p §2. คุณสมบัติของการแปลง Laplace ต่อไปนี้เราจะแสดงถึงฟังก์ชันดั้งเดิมและผ่าน - รูปภาพตาม Laplace biw dee เป็นฟังก์ชันที่ต่อเนื่องกัน) มีอิมเมจเหมือนกัน แล้วพวกมันจะเท่ากัน Teopewa 3 (n "yeyiost * เปลี่ยน Laplace) หากฟังก์ชันนั้นเป็นฟังก์ชันดั้งเดิม สำหรับค่าคงที่ที่ซับซ้อนใดๆ ของอากาศ ความถูกต้องของคำสั่งจะตามมาจากคุณสมบัติลิเนียริตี้ของอินทิกรัลที่กำหนดรูปภาพ: คืออัตราการเติบโตของฟังก์ชันตามลำดับ) จากคุณสมบัตินี้ เราได้รับ ในทำนองเดียวกัน เราพบว่าและเพิ่มเติม ทฤษฎีบท 4 (ความคล้ายคลึงกัน) ถ้า f (t) เป็นฟังก์ชันดั้งเดิมและ F (p) เป็นอิมเมจ Laplace ดังนั้นสำหรับค่าคงที่ใดๆ a> 0 การใส่ที่ = m เรามีการใช้ทฤษฎีบทนี้ จากสูตร (5) และ (6) เราจะได้ทฤษฎีบท 5 (บนความแตกต่างของต้นฉบับ). อนุญาต เป็นฟังก์ชันดั้งเดิมด้วยภาพ F (p) และ อนุญาต - เป็นฟังก์ชันดั้งเดิมด้วย และอัตราการเติบโตของฟังก์ชันอยู่ที่ไหน จากนั้นและโดยทั่วไป ในที่นี้ เราหมายถึงค่าจำกัดที่ถูกต้อง อนุญาต ให้เราหาภาพ เรามีการ Integrating ตามส่วนต่างๆ เราจะได้ The non-integral ทางด้านขวามือของ (10) หายไปที่ k สำหรับ Rc p = s> h เรามีการแทนที่ t = Odet - / ( 0). เทอมที่สองทางด้านขวาใน (10) เท่ากับ pF (p) ดังนั้น ความสัมพันธ์ (10) จึงมีรูปแบบและสูตร (8) ได้รับการพิสูจน์แล้ว โดยเฉพาะอย่างยิ่ง ถ้า ในการหาภาพ f (n \ t) เราเขียนว่ามาจากไหน รวม n ครั้งโดยส่วนต่างๆ เราจะได้ตัวอย่างที่ 4 ใช้ทฤษฎีบทในการแยกแยะของต้นฉบับ หาภาพของฟังก์ชัน f (t) = บาป2 ต. ให้ ดังนั้น ทฤษฎีบท 5 ได้กำหนดคุณสมบัติที่โดดเด่นของการแปลงอินทิกรัล Laplace: มัน (เช่นการแปลงฟูริเยร์) เปลี่ยนการดำเนินการของดิฟเฟอเรนติเอชันเป็นการดำเนินการเกี่ยวกับพีชคณิตของการคูณด้วย p รวมสูตร. หากเป็นฟังก์ชันดั้งเดิม แท้จริงแล้ว โดยอาศัยผลที่ตามมาของทฤษฎีบท 1 ทุกภาพมักจะมีค่าเป็นศูนย์ ดังนั้นสูตรการรวมจึงตามมา (ทฤษฎีบท 6 (บนความแตกต่างของภาพ) ความแตกต่างของภาพจะลดลงเป็นการคูณด้วยต้นฉบับเนื่องจากฟังก์ชัน F (p) ในครึ่งระนาบจึงเป็นการวิเคราะห์จึงสามารถ แตกต่างด้วยความเคารพ p. เรามีหลังแค่หมายถึง ตัวอย่างที่ 5 ใช้ทฤษฎีบท 6 ค้นหาภาพของฟังก์ชัน 4 ตามที่ทราบ ดังนั้น (เมื่อใช้ทฤษฎีบท 6 อีกครั้ง เราพบว่าโดยทั่วไปแล้ว ทฤษฎีบท 7 (การรวมของต้นฉบับ) . การรวมของต้นฉบับจะลดลงเพื่อแบ่งภาพโดย Let It ง่ายต่อการตรวจสอบว่าหากมีฟังก์ชั่นดั้งเดิมแล้วจะเป็นฟังก์ชั่นดั้งเดิมยิ่งกว่านั้น ปล่อยให้เป็น โดยอาศัยอำนาจตามนั้น ในทางกลับกัน เมื่อ F = ตัวหลังเทียบเท่ากับความสัมพันธ์ที่พิสูจน์แล้ว (13) ตัวอย่างที่ 6 ค้นหาภาพของฟังก์ชัน M ในกรณีนี้ ดังนั้น ดังนั้น ทฤษฎีบท 8 (การรวมภาพ) ถ้าอินทิกรัลมาบรรจบกัน ก็จะทำหน้าที่เป็นรูปภาพของฟังก์ชัน ^: LAPLACE TRANSFORM คำจำกัดความพื้นฐาน คุณสมบัติ Convolution of functions ทฤษฎีบทการคูณ การหาต้นฉบับจากภาพ การใช้ทฤษฎีบทผกผันสำหรับแคลคูลัสปฏิบัติการ สูตรของ Duhamel การบูรณาการระบบของสมการอนุพันธ์เชิงเส้นกับ สัมประสิทธิ์คงที่ แก้สมการปริพันธ์ อันที่จริง สมมติว่าเส้นทางของการบูรณาการอยู่บนระนาบครึ่งระนาบ ดังนั้น เราสามารถเปลี่ยนลำดับของการรวมกันได้ ความเสมอภาคสุดท้ายหมายความว่ามันเป็นภาพของฟังก์ชัน ตัวอย่างที่ 7 ค้นหาภาพของ a ฟังก์ชั่น M ตามที่ทราบ,. ดังนั้น เนื่องจากเราใส่ เราได้รับ £ = 0 สำหรับ ดังนั้นความสัมพันธ์ (16) จึงอยู่ในรูปแบบ ตัวอย่าง ค้นหาภาพของฟังก์ชัน f (t) ในรูปกราฟิก (รูปที่ 5) ลองเขียนนิพจน์สำหรับฟังก์ชัน f (t) กันดังนี้ นิพจน์นี้สามารถหาได้ดังนี้ พิจารณาฟังก์ชันแล้วลบฟังก์ชันออกจากฟังก์ชันนั้น ผลต่าง จะเท่ากับ 1 สำหรับ เราเพิ่มฟังก์ชันให้กับผลต่างที่เป็นผลลัพธ์ ด้วยเหตุนี้ เราจึงได้ฟังก์ชัน f (t) (รูปที่ 6c) ดังนั้น จากที่นี่ โดยใช้ทฤษฎีบทการหน่วงเวลา เราจะพบ Theorem 10 (displacement) จากนั้นสำหรับจำนวนเชิงซ้อน p0 อันที่จริง ทฤษฎีบทนี้อนุญาตให้ค้นหารูปภาพของฟังก์ชันเดียวกันคูณด้วยฟังก์ชันเลขชี้กำลังจากรูปภาพที่ทราบของฟังก์ชันได้ เช่น 2.1 การบิดของฟังก์ชัน ทฤษฎีบทการคูณ ให้ฟังก์ชัน f (t) u ถูกกำหนดและต่อเนื่องสำหรับ t ทั้งหมด การบิดของฟังก์ชันเหล่านี้เรียกว่า ฟังก์ชั่นใหม่จาก t กำหนดโดยความเท่าเทียมกัน (ถ้าอินทิกรัลนี้มีอยู่) สำหรับฟังก์ชันดั้งเดิม การดำเนินการจะยุบได้เสมอ และ (17) 4 อันที่จริง ผลคูณของฟังก์ชันดั้งเดิมในฐานะฟังก์ชันของ m เป็นฟังก์ชันจำกัด กล่าวคือ หายไปนอกช่วงจำกัด (ในกรณีนี้ นอกช่วง สำหรับฟังก์ชันต่อเนื่องจำกัด การดำเนินการ convolution เป็นที่พอใจ และเราได้สูตร มันง่ายที่จะตรวจสอบว่าการดำเนินการ convolution เป็นการสับเปลี่ยน ทฤษฎีบท 11 (การคูณ) ถ้า จากนั้นการโค้งงอ t) มีภาพที่การโค้งงอ (ของฟังก์ชั่นดั้งเดิมคือฟังก์ชั่นดั้งเดิมที่มีเลขชี้กำลังการเติบโต "โดยที่, เป็นเลขชี้กำลังการเจริญเติบโตของฟังก์ชันตามลำดับ ลองหาภาพของการโค้งงอโดยใช้สิ่งที่เรามี การเปลี่ยนแปลง ลำดับของการบูรณาการในอินทิกรัลทางด้านขวา (การดำเนินการดังกล่าวถูกกฎหมาย) และใช้ทฤษฎีบทการหน่วงเวลา เราได้รับ ดังนั้นจาก (18) และ (19) เราพบว่าการคูณของภาพสอดคล้องกับการบิดของต้นฉบับ Prter 9. หาภาพของฟังก์ชัน A ฟังก์ชัน V (0 คือการบิดของฟังก์ชัน โดยทฤษฎีบทการคูณ ปัญหา ให้ฟังก์ชัน f (t) เป็นคาบที่มีคาบ T , ecg เป็นฟังก์ชันดั้งเดิม แสดงว่า Laplace image F (p) กำหนดโดยสูตรที่ 3 การหาต้นฉบับจากภาพ โจทย์มีดังนี้ สำหรับฟังก์ชัน F (p) เราต้องหาฟังก์ชัน / (<)>ซึ่งมีรูปคือ F (p) ให้เรากำหนดเงื่อนไขที่เพียงพอสำหรับฟังก์ชัน F (p) ของตัวแปรเชิงซ้อน p เพื่อทำหน้าที่เป็นรูปภาพ ทฤษฎีบท 12. ถ้าฟังก์ชัน F (p) 1) วิเคราะห์ในครึ่งระนาบ ดังนั้น มีแนวโน้มว่าจะเป็นศูนย์สำหรับในครึ่งระนาบ R s0 อย่างสม่ำเสมอเมื่อเทียบกับหาเรื่อง p; 2) อินทิกรัลมาบรรจบกันโดยสิ้นเชิง จากนั้น F (p) เป็นภาพของปัญหาฟังก์ชันดั้งเดิมบางอย่าง ฟังก์ชัน F (p) = ใช้เป็นรูปภาพของฟังก์ชันดั้งเดิมได้หรือไม่ ต่อไปนี้เป็นวิธีค้นหาต้นฉบับจากรูปภาพ 3.1. การค้นหาต้นฉบับโดยใช้ตารางรูปภาพ ก่อนอื่น การนำฟังก์ชัน F (p) ไปใช้ในรูปแบบ "ตาราง" ที่เรียบง่ายกว่านั้นคุ้มค่า ตัวอย่างเช่น ในกรณีที่ F (p) เป็นฟังก์ชันตรรกยะที่เป็นเศษส่วนของอาร์กิวเมนต์ p ฟังก์ชันนี้จะสลายตัวเป็นเศษส่วนพื้นฐานและใช้คุณสมบัติที่เหมาะสมของการแปลงลาปลาซ ตัวอย่างที่ 1 ค้นหาต้นฉบับสำหรับ Let us เขียนฟังก์ชัน F (p) ในรูปแบบ โดยใช้ทฤษฎีบทการกระจัดและคุณสมบัติเชิงเส้นของการแปลง Laplace เราได้ตัวอย่างที่ 2 ค้นหาต้นฉบับสำหรับฟังก์ชัน 4 ให้เราเขียน F (p ) ดังเช่น 3.2 การใช้ทฤษฎีบทผกผันและผลที่ตามมา ทฤษฎีบท 13 (ผกผัน) ถ้าฟังก์ชันพอดี) เป็นฟังก์ชันดั้งเดิมที่มีเลขชี้กำลังการเติบโต s0 และ F (p) เป็นรูปภาพ ดังนั้น ณ จุดใด ๆ ของความต่อเนื่องของฟังก์ชัน f (t) ความสัมพันธ์จะคงอยู่โดยที่อินทิกรัลถูกนำไปตามเส้นตรงใดๆ และเป็นที่เข้าใจ ในความหมายของค่าหลัก กล่าวคือ สูตร (1) เรียกว่า สูตรผกผัน Laplace transform หรือสูตรของ Mellin ยกตัวอย่างเช่น f (t) เรียบเป็นชิ้นเล็กชิ้นน้อยในทุกส่วน จำกัด โดยที่< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
8 การบรรยาย 7 ฟังก์ชันผู้ปฏิบัติงานของวงจร ฟังก์ชันอินพุตและการถ่ายโอนของผู้ดำเนินการ ขั้วและศูนย์ของฟังก์ชันวงจร 3 บทสรุป ฟังก์ชันอินพุตและการถ่ายโอนของตัวดำเนินการ ฟังก์ชันตัวดำเนินการของโซ่เป็นความสัมพันธ์
68 การบรรยายที่ 7 กระบวนการเปลี่ยนผ่านในวงจรลำดับที่หนึ่ง แผน 1 กระบวนการชั่วคราวในวงจร RC ของลำดับที่หนึ่ง 2 กระบวนการชั่วคราวในวงจร R ของลำดับแรก 3 ตัวอย่างการคำนวณกระบวนการชั่วคราวในวงจร
4 วงจรไฟฟ้าเชิงเส้นของกระแสไฟ AC ไซนูซอยด์และวิธีการคำนวณ 4.1 เครื่องจักรไฟฟ้า หลักการสร้างกระแสไซนูซอยด์ 4.1.012 กระแสไซนัสเรียกว่าทันที
หน่วยงานของรัฐบาลกลางเพื่อการศึกษา สถาบันการศึกษาระดับอุดมศึกษาของรัฐ "มหาวิทยาลัย KUBAN STATE" คณะฟิสิกส์และเทคโนโลยี ภาควิชาออปโตอิเล็กทรอนิกส์
~ ~ FKP Derivative ของฟังก์ชันของตัวแปรเชิงซ้อน FKP ของ Cauchy - Riemann ให้เงื่อนไขแนวคิดเรื่องความสม่ำเสมอของ FKP Image และรูปแบบของจำนวนเชิงซ้อน รูปแบบของ FKP: โดยที่ฟังก์ชันที่แท้จริงของตัวแปรสองตัวนั้นเป็นของจริง
 Odnoklassniki: การลงทะเบียนและการสร้างโปรไฟล์
Odnoklassniki: การลงทะเบียนและการสร้างโปรไฟล์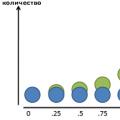 อีคือ E (ฟังก์ชัน E) นิพจน์ในแง่ของฟังก์ชันตรีโกณมิติ
อีคือ E (ฟังก์ชัน E) นิพจน์ในแง่ของฟังก์ชันตรีโกณมิติ โซเชียลเน็ตเวิร์กของรัสเซียตอนนี้อยู่ในโซเชียลเน็ตเวิร์ก
โซเชียลเน็ตเวิร์กของรัสเซียตอนนี้อยู่ในโซเชียลเน็ตเวิร์ก