Kendall Rank Correlation Coefficient. Kendallův koeficient pořadové korelace. Podívejte se, co je to "Kendallův koeficient korelace pořadí" v jiných slovnících
Kendallův korelační koeficient se používá, když jsou proměnné reprezentovány dvěma ordinálními stupnicemi, za předpokladu, že neexistují žádné asociované úrovně. Výpočet Kendallova koeficientu je spojen s počítáním počtu shod a inverzí. Uvažujme tento postup na příkladu předchozího problému.
Algoritmus pro řešení problému je následující:
Přeformátujeme data tabulky. 8.5 tak, aby jeden z řádků (v tomto případě řádek X i) byl zařazen. Jinými slovy, vyměňujeme páry X a y ve správném pořadí a zadáváme údaje do sloupců 1 a 2 tabulky. 8.6.
Tabulka 8.6
|
X i |
y i | ||
2. Určete „stupeň hodnocení“ 2. řádku ( y i). Tento postup se provádí v následujícím pořadí:
a) vzít první hodnotu nezařazené řady „3“. Počítání počtu hodností níže dané číslo, které více porovnávaná hodnota. Existuje 9 takových hodnot (čísla 6, 7, 4, 9, 5, 11, 8, 12 a 10). Do kolonky "náhoda" zapíšeme číslo 9. Poté spočítáme počet hodnot, které menší tři. Existují 2 takové hodnoty (řady 1 a 2); zadejte číslo 2 do sloupce "inverze".
b) vyhoďte číslo 3 (už jsme s ním pracovali) a opakujte postup pro další hodnotu „6“: počet shod je 6 (řady 7, 9, 11, 8, 12 a 10), počet shod. inverze je 4 (řady 1, 2, 4 a 5). Do sloupce „náhoda“ zadáme číslo 6 a do sloupce „inverze“ číslo 4.
c) obdobným způsobem se postup opakuje až do konce řady; je třeba mít na paměti, že každá „vypracovaná“ hodnota je vyloučena z dalšího posuzování (počítány jsou pouze pořadí, které leží pod tímto číslem).
Poznámka
Aby nedošlo k chybám ve výpočtech, je třeba mít na paměti, že s každým „krokem“ se součet náhod a inverzí o jednu snižuje; to je pochopitelné vzhledem k tomu, že pokaždé je jedna hodnota vyloučena z úvahy.
3. Vypočítá se součet zápasů (R) a součet inverzí (Q); data se zadávají do jednoho a tří zaměnitelných vzorců Kendallova koeficientu (8.10). Provedou se odpovídající výpočty.
t (8.10)
V našem případě:
V tabulce. XIV Aplikace jsou kritické hodnoty koeficientu pro daný vzorek: τ cr. = 0,45; 0,59. Empiricky získaná hodnota je porovnána s tabulkovou hodnotou.
Závěr
τ = 0,55 > τ kr. = 0,45. Pro úroveň 1 je korelace statisticky významná.
Poznámka:
V případě potřeby (například při absenci tabulky kritických hodnot) statistická významnost t Kendall lze definovat vzorcem, jako je tento:
 (8.11)
(8.11)
kde S* = P - Q+ 1 pokud P< Q , a S* = P - Q - 1 pokud P > Q.
Hodnoty z pro odpovídající hladinu významnosti odpovídají Pearsonově míře a jsou nalezeny podle odpovídajících tabulek (nejsou součástí přílohy. Pro standardní hladiny významnosti z cr = 1,96 (pro p1 = 0,95) a 2,58 (pro p2 = 0,99). Kendallův korelační koeficient je statisticky významný, jestliže z > z kr
V našem případě S* = P - Q– 1 = 35 a z= 2,40, tj. potvrzuje se výchozí závěr: korelace mezi znaky je statisticky významná pro 1. hladinu významnosti.
Při řazení musí expert seřadit hodnocené prvky ve vzestupném (sestupném) pořadí podle jejich preference a každému z nich přiřadit pořadí ve formě přirozených čísel. V přímém hodnocení má nejpreferovanější položka hodnost 1 (někdy 0) a nejméně preferovaná položka má hodnost m.
Pokud odborník nemůže provést přísné hodnocení z důvodu, že podle jeho názoru jsou některé prvky přednostně stejné, je povoleno těmto prvkům přiřadit stejné pořadí. Aby byl součet hodností roven součtu míst hodnocených prvků, používají se tzv. standardizované hodnosti. Standardizované pořadí je aritmetický průměr počtu prvků v hodnocené řadě, které jsou preferovány stejně.
Příklad 2.6. Expert seřadil šest položek podle preferencí takto:
Pak budou standardizované řady těchto prvků
Součet úrovní přiřazených prvkům se tedy bude rovnat součtu přirozených čísel.
Přesnost vyjádření preference klasifikačními prvky významně závisí na mohutnosti souboru prezentací. Postup hodnocení dává nejspolehlivější výsledky (podle míry blízkosti odhalené preference a „pravda“), kdy počet hodnocených prvků není větší než 10. Limitující síla prezentační sady by neměla překročit 20.
Zpracování a analýza žebříčků se provádí za účelem vybudování skupinového preferenčního vztahu na základě individuálních preferencí. V tomto případě lze stanovit následující úkoly: a) určení těsnosti souvislosti mezi hodnocením dvou expertů na prvky souboru prezentací; b) určení vztahu mezi dvěma prvky podle individuálních názorů členů skupiny na různé charakteristiky těchto prvků; c) posouzení shody názorů odborníků ve skupině složené z více než dvou odborníků.
V prvních dvou případech se koeficient používá jako míra těsnosti vztahu hodnostní korelace. V závislosti na tom, zda je povoleno pouze přísné nebo nepřísné hodnocení, se použije buď Kendallův nebo Spearmanův koeficient pořadové korelace.
Kendallův korelační koeficient pro problém (a)
kde m− počet prvků; r 1 i – hodnost přidělená prvním expertem i-tý prvek; r 2 i – tentýž, druhý odborník.
Pro úlohu (b) mají složky (2.5) následující význam: m je počet charakteristik dvou hodnocených prvků; r 1 i(r 2 i) - hodnost i-tá charakteristika v pořadí prvního (druhého) prvku sestaveného skupinou odborníků.
Přísné hodnocení používá koeficient pořadové korelace R Spearman:
jejichž složky mají stejný význam jako v (2.5).
Korelační koeficienty (2,5), (2,6) se pohybují od -1 do +1. Pokud je korelační koeficient +1, znamená to, že pořadí je stejné; pokud se rovná -1, pak − jsou opačné (hodnocení jsou vzájemně inverzní). Rovnost korelačního koeficientu na nulu znamená, že hodnocení jsou lineárně nezávislá (nekorelovaná).
Protože u tohoto přístupu (expert je „měřicí nástroj“ s náhodnou chybou) jsou jednotlivá pořadí považována za náhodná, vyvstává problém statistického testování hypotézy o významnosti získaného korelačního koeficientu. V tomto případě se používá Neyman-Pearsonův test: jsou stanoveny hladinou významnosti kritéria α a se znalostí distribučních zákonů korelačního koeficientu určují prahovou hodnotu. ca, se kterou se porovnává získaná hodnota korelačního koeficientu. Kritická oblast je pravotočivá (v praxi se obvykle nejprve vypočítá hodnota kritéria a z ní se určí hladina významnosti, která se porovná s prahovou hladinou α ).
Koeficient pořadové korelace τ Kendall má pro m > 10 rozdělení blízké normálu s následujícími parametry:
kde M [τ] je matematické očekávání; D [τ] je disperze.
V tomto případě se používají tabulky funkce standardního normálního rozdělení:
a hranice τ α kritické oblasti je definována jako kořen rovnice
Pokud je vypočtená hodnota koeficientu τ ≥ τ α , pak se má za to, že pořadí jsou ve skutečně dobré shodě. Typicky se hodnota a volí v rozmezí 0,01-0,05. Pro m ≤ 10 je rozdělení m uvedeno v tabulce. 2.1.
Kontrola významnosti konzistence dvou hodnocení pomocí Spearmanova koeficientu ρ se provádí ve stejném pořadí pomocí Studentových distribučních tabulek pro m > 10.
V tomto případě hodnota
má distribuci dobře přibližnou distribuci studenta s m– 2 stupně volnosti. V m> 30, rozdělení ρ je v dobré shodě s normálním, které má M [ρ] = 0 a D [ρ] = .
Pro m ≤ 10 je významnost ρ ověřena pomocí tabulky. 2.2.
Pokud není žebříček přísný, tak Spearmanův koeficient
kde ρ se vypočítá podle (2.6);
kde k 1, k 2 je počet různých skupin nepřísných řad v prvním a druhém pořadí; l i je počet stejných pozic v i-tá skupina. Při praktickém použití Spearmanových koeficientů hodnostní korelace ρ a Kendallova τ je třeba mít na paměti, že koeficient ρ poskytuje přesnější výsledek z hlediska minimálního rozptylu.
Tabulka 2.1.Rozdělení Kendallova koeficientu pořadové korelace
Prezentace a předzpracování znaleckých posudků
V praxi se používá několik typů hodnocení:
- kvalita (často-zřídka, horší-lepší, ano-ne),
- skóre stupnice (rozsahy hodnot 50-75, 76-90, 91-120 atd.),
Skóre z daného intervalu (od 2 do 5, 1 -10), vzájemně nezávislé,
Hodnoceno (objekty jsou řazeny odborníkem v určitém pořadí a každému je přiděleno pořadové číslo - hodnost),
Srovnávací získaný jednou ze srovnávacích metod
metoda postupného srovnávání
metoda párového porovnávání faktorů.
V dalším kroku zpracování znaleckých posudků je nutné vyhodnotit míra shody mezi těmito názory.
Odhady získané od expertů lze považovat za náhodnou veličinu, jejíž rozložení odráží názory expertů na pravděpodobnost té či oné volby události (faktoru). Proto se k analýze rozptylu a konzistence odborných odhadů používají zobecněné statistické charakteristiky - průměry a rozptylové míry:
střední kvadratická chyba,
Rozsah variace min - max,
- variační koeficient V \u003d rms. devi. / aritm. průměr. (vhodné pro jakýkoli typ hodnocení)
V i = σ i / x i srov
Pro sazbu míry podobnosti ale názory každá dvojice odborníků Lze použít různé metody:
asociační koeficienty, které zohledňují počet shodných a neshodných odpovědí,
koeficienty nekonzistence znalecké posudky,
Všechna tato měřítka lze použít buď k porovnání názorů dvou expertů, nebo k analýze vztahu mezi řadou odhadů podle dvou kritérií.
Spearmanův párový korelační koeficient:
kde n je počet odborníků,
c k je rozdíl mezi odhady i-tého a j-tého experta pro všechny T faktory
Kendallův koeficient pořadové korelace (koeficient shody) dává celkové hodnocení konzistence názorů všech odborníků na všechny faktory, ale pouze pro případy, kdy byly použity odhady pořadí.
Je prokázáno, že hodnota S, když všichni experti posuzují všechny faktory stejně, má maximální hodnotu rovnou
kde n je počet faktorů,
m je počet odborníků.
Koeficient shody se rovná poměru
navíc, pokud se W blíží 1, pak všichni experti poskytli poměrně konzistentní odhady, jinak jsou jejich názory nekonzistentní.
Vzorec pro výpočet S je uveden níže:
kde r ij - hodnocení odhadů i-tého faktoru j-tým expertem,
r cf - průměrné pořadí v celé matici odhadů a je rovno
A proto vzorec pro výpočet S může mít tvar:
Pokud se jednotlivá hodnocení jednoho znalce shodují a při zpracování byla standardizována, použije se pro výpočet koeficientu shody jiný vzorec:
kde Tj se vypočítá pro každého odborníka (v případě, že jeho posouzení byla opakována pro různé objekty), s přihlédnutím k opakování podle následujících pravidel:
kde t j je počet skupin stejné úrovně pro j-tého odborníka a
h k - počet stejných řad v k-té skupině příbuzných řad j-tého odborníka.
PŘÍKLAD. Nechte 5 odborníků na šest faktorů reagovat při hodnocení podle tabulky 3:
Tabulka 3 – Odpovědi odborníků
| Odborníci | O1 | O2 | O3 | O4 | O5 | O6 | Součet hodnocení podle experta |
| E1 | |||||||
| E2 | |||||||
| E3 | |||||||
| E4 | |||||||
| E5 |
Vzhledem k tomu, že bylo získáno nepřísné pořadí (odhady odborníků se opakují a součty pořadí se nerovnají), provedeme transformaci odhadů a získáme související pořadí (tabulka 4):
Tabulka 4 - Související pořadí expertních hodnocení
| Odborníci | O1 | O2 | O3 | O4 | O5 | O6 | Součet hodnocení podle experta |
| E1 | 2,5 | 2,5 | |||||
| E2 | |||||||
| E3 | 1,5 | 1,5 | 4,5 | 4,5 | |||
| E4 | 2,5 | 2,5 | 4,5 | 4,5 | |||
| E5 | 5,5 | 5,5 | |||||
| Součet hodností podle objektu | 7,5 | 9,5 | 23,5 | 29,5 |
Nyní určíme míru shody mezi názory znalců pomocí koeficientu shody. Vzhledem k tomu, že pořadí spolu souvisí, vypočítáme W pomocí vzorce (**).
Potom r cf \u003d 7 * 5 / 2 \u003d 17,5
S = 10 2 +8 2 +4,5 2 +4,5 2 +6 2 +12 2 = 384,5
Přejděme k výpočtu W. K tomu vypočítáme samostatně hodnoty T j . V příkladu jsou známky speciálně vybrány tak, že každý znalec má opakované známky: 1. má dvě, druhý má tři, třetí má dvě skupiny po dvou známkách, čtvrtý a pátý mají dvě stejné známky. Odtud:
T 1 \u003d 2 3 – 2 \u003d 6 T 5 \u003d 6
T 2 \u003d 3 3 - 3 \u003d 24
T 3 \u003d 2 3 -2+ 2 3 -2 \u003d 12 T 4 \u003d 12
Vidíme, že shoda v názorech odborníků je poměrně vysoká a je možné přistoupit k další fázi studie - zdůvodnění a přijetí alternativního řešení doporučeného odborníky.
V opačném případě se musíte vrátit ke krokům 4-8.
Jedním z faktorů omezujících použití kritérií založených na předpokladu normality je velikost vzorku. Pokud je vzorek dostatečně velký (například 100 nebo více pozorování), můžete předpokládat, že rozložení vzorku je normální, i když si nejste jisti, že rozložení proměnné v populaci je normální. Pokud je však vzorek malý, měly by být tyto testy použity pouze v případě, že existuje jistota, že proměnná je skutečně normálně distribuována. Neexistuje však způsob, jak tento předpoklad otestovat na malém vzorku.
Použití kritérií vycházejících z předpokladu normality je také omezeno měřítkem měření (viz kapitola Základní pojmy analýzy dat). Statistické metody jako t-test, regrese atd. předpokládají, že původní data jsou spojitá. Existují však situace, kdy jsou data jednoduše řazena (měřena na ordinální stupnici), spíše než přesně měřena.
Typickým příkladem je hodnocení stránek na internetu: na první pozici je stránka s maximálním počtem návštěvníků, na druhé pozici je stránka s maximální návštěvností mezi zbývajícími stránkami (mezi stránkami, ze kterých první stránka byla odstraněna) atd. Se znalostí hodnocení můžeme říci, že návštěvnost jedné stránky je větší než návštěvnost jiné stránky, ale o kolik více, nelze říci. Představte si, že máte 5 webů: A, B, C, D, E, které se nacházejí na prvních 5 místech. Předpokládejme, že v aktuálním měsíci jsme měli toto uspořádání: A, B, C, D, E a v předchozím měsíci: D, E, A, B, C. Otázkou je, zda došlo k výrazným změnám v hodnocení stránek nebo ne? V této situaci samozřejmě nemůžeme použít t-test k porovnání těchto dvou souborů dat a přesouváme se do oblasti konkrétních pravděpodobnostních výpočtů (a každý statistický test obsahuje pravděpodobnostní výpočet!). Uvažujeme přibližně takto: jak pravděpodobné je, že rozdíl v uspořádání dvou míst je způsoben čistě náhodnými důvody, nebo je tento rozdíl příliš velký a nelze jej vysvětlit čirou náhodou. V těchto diskuzích používáme pouze hodnocení nebo permutace stránek a nepoužíváme konkrétní typ rozložení počtu návštěvníků na nich.
Pro analýzu malých vzorků a pro data naměřená na špatných měřítcích se používají neparametrické metody.
Stručný přehled neparametrických postupů
V podstatě pro každé parametrické kritérium existují alespoň, jedna neparametrická alternativa.
Obecně tyto postupy spadají do jedné z následujících kategorií:
- rozdílová kritéria pro nezávislé vzorky;
- rozdílová kritéria pro závislé vzorky;
- posouzení míry závislosti mezi proměnnými.
Obecně by měl být přístup ke statistickým kritériím při analýze dat pragmatický a nezatížený zbytečnými teoretickými úvahami. S počítačem STATISTICA, který máte k dispozici, můžete na svá data snadno aplikovat několik kritérií. S vědomím některých úskalí metod si vyberete správné řešení pomocí experimentování. Vývoj grafu je zcela přirozený: pokud potřebujete porovnat hodnoty dvou proměnných, použijte t-test. Je však třeba připomenout, že je založen na předpokladu normality a rovnosti rozptylů v každé skupině. Osvobození od těchto předpokladů vede k neparametrickým testům, které jsou užitečné zejména pro malé vzorky.
Vývoj t-testu vede k analýze rozptylu, která se používá, když je počet porovnávaných skupin větší než dvě. Odpovídající vývoj neparametrických postupů vede k neparametrické analýze rozptylu, i když je mnohem horší než klasická analýza rozptylu.
Pro posouzení závislosti, nebo, poněkud velkolepě řečeno, míry těsnosti souvislosti se počítá Pearsonův korelační koeficient. Přísně vzato má jeho použití omezení spojená např. s typem škály, ve které jsou data měřena a nelinearitou závislosti, proto jako alternativa neparametrické, nebo tzv. hodnostní, korelační koeficienty. se také používají, které se používají například pro řazená data. Pokud jsou data měřena na nominálním měřítku, pak je přirozené je prezentovat v kontingenčních tabulkách, které využívají Pearsonův chí-kvadrát test s různými variacemi a úpravami pro přesnost.
V podstatě tedy existuje jen několik typů kritérií a postupů, které musíte znát a umět je používat, v závislosti na specifikách dat. Musíte určit, jaké kritérium by se mělo v konkrétní situaci použít.
Neparametrické metody jsou nejvhodnější, pokud je velikost vzorku malá. Pokud existuje mnoho dat (například n > 100), často nemá smysl používat neparametrické statistiky.
Pokud je velikost vzorku velmi malá (například n = 10 nebo méně), lze hladiny významnosti pro ty neparametrické testy, které používají normální aproximaci, považovat pouze za hrubé odhady.
Rozdíly mezi nezávislými skupinami. Pokud existují dva vzorky (např. muži a ženy), které je třeba porovnat s ohledem na nějakou střední hodnotu, jako je průměrný krevní tlak nebo počet bílých krvinek, pak lze použít nezávislý vzorkový t-test.
Neparametrické alternativy k tomuto testu jsou Wald-Wolfowitz, Mann-Whitney )/n série test, kde x i - i-tá hodnota, n - počet pozorování. Pokud proměnná obsahuje záporné hodnoty nebo nulu (0), geometrický průměr nelze vypočítat.
Harmonický průměr
Harmonický průměr se někdy používá k průměrování frekvencí. Harmonický průměr se vypočítá podle vzorce: HS = n/S(1/x i) kde HS je harmonický průměr, n je počet pozorování, x i je hodnota pozorování s číslem i. Pokud proměnná obsahuje nulu (0), nelze harmonický průměr vypočítat.
Rozptyl a směrodatná odchylka
Výběrový rozptyl a směrodatná odchylka jsou nejčastěji používanými měřítky variability (variací) v datech. Rozptyl se vypočítá jako součet čtverců odchylek hodnot proměnné od výběrového průměru dělený n-1 (ale ne n). Směrodatná odchylka se vypočítá jako druhá odmocnina odhadu rozptylu.
rozsah
Rozsah proměnné je mírou volatility, počítá se jako maximum mínus minimum.
Kvartilový rozsah
Čtvrtletní rozmezí podle definice je: horní kvartil mínus spodní kvartil (75% percentil mínus 25% percentil). Protože percentil 75 % (horní kvartil) je hodnota nalevo, od níž je 75 % pozorování, a percentil 25 % (dolní kvartil) je hodnota nalevo od níž je 25 % pozorování, kvartil rozsah je interval kolem mediánu, který obsahuje 50 % pozorování (hodnot proměnné).
Asymetrie
Šikmost je charakteristická pro tvar distribuce. Distribuce je zkosená doleva, pokud je zešikmení záporné. Distribuce je zkosená doprava, pokud je šikmost kladná. Šikmost standardního normálního rozdělení je 0. Šikmost se vztahuje ke třetímu momentu a je definována jako: šikmost = n × M 3 /[(n-1) × (n-2) × s 3 ], kde M 3 je: (x i -xstřední x) 3, s 3 - standardní odchylka zvýšená na třetí mocninu, n - počet pozorování.
Přebytek
Kurtóza je charakteristika tvaru rozdělení, konkrétně míra ostrosti jeho vrcholu (ve vztahu k normálnímu rozdělení, jehož špičatost je 0). Obecně platí, že distribuce s ostřejším vrcholem než normální distribuce mají kladnou špičatost; rozdělení, jejichž vrchol je méně ostrý než vrchol normálního rozdělení, mají zápornou špičatost. Kurtóza je spojena se čtvrtým momentem a je určena vzorcem:
kurtosis = /[(n-1) × (n-2) × (n-3) × s 4 ], kde M j je: (x-x průměr x, s 4 je standardní odchylka od čtvrté mocniny, n je počet pozorování.
Pořadový korelační koeficient charakterizuje obecnou povahu nelineární závislosti: zvýšení nebo snížení výsledného znaménka se zvýšením faktoriálu. To je indikátor těsnosti monotónního nelineárního vztahu.Přiřazení služby. Tato online kalkulačka počítá Kendalův koeficient pořadové korelace pro všechny základní vzorce a také posouzení jeho významu.
Návod. Zadejte množství dat (počet řádků). Výsledné řešení se uloží do souboru aplikace Word.
Koeficient navržený Kendallem je postaven na základě vztahů typu „více-méně“, jejichž platnost byla stanovena při konstrukci škál.
Vyberme si pár objektů a porovnejme jejich pořadí podle jednoho atributu a podle druhého. Pokud pořadí tvoří přímé pořadí podle tohoto znaku (tj. pořadí přirozené řady), pak je dvojici přiřazeno +1, pokud je opačné, pak -1. Pro vybraný pár se vynásobí odpovídající jednotky plus-minus (podle prvku X a podle prvku Y). Výsledek je zjevně +1; pokud jsou pořadí dvojice obou prvků ve stejném pořadí, a -1, pokud jsou v opačném pořadí.
Pokud jsou pořadí obou prvků stejné pro všechny páry, pak je součet jednotek přiřazených všem párům objektů maximální a roven počtu párů. Pokud jsou pořadí všech párů obrácená, pak –C 2 N . V obecném případě C 2 N = P + Q, kde P je počet kladných a Q záporných jednotek přiřazených párům při porovnání jejich pořadí pro oba znaky.
Hodnota se nazývá Kendallův koeficient.
Ze vzorce je vidět, že koeficient τ je rozdíl mezi podílem dvojic objektů, které mají v obou znacích stejné pořadí (ve vztahu k počtu všech dvojic), a podílem dvojic objektů, které nemají stejné pořadí.
Například hodnota koeficientu 0,60 znamená, že 80 % párů má stejné pořadí objektů a 20 % nikoli (80 % + 20 % = 100 %; 0,80 - 0,20 = 0,60). Tito. τ lze interpretovat jako rozdíl mezi pravděpodobnostmi koincidence a nekoincidence řádů v obou rysech pro náhodně vybranou dvojici objektů.
V obecném případě se výpočet τ (přesněji P nebo Q), a to i pro N v řádu 10, ukazuje jako těžkopádný.
Pojďme si ukázat, jak zjednodušit výpočty.
![]()
![]()
Příklad. Vztah mezi objemem průmyslové výroby a investicemi do fixního kapitálu v 10 regionech jednoho z federálních okresů Ruské federace v roce 2003 charakterizují následující údaje:
Vypočítejte koeficienty korelace pořadí podle Spearmana a Kendalla. Zkontrolujte jejich významnost při α=0,05. Formulujte závěr o vztahu mezi objemem průmyslové výroby a investicemi do stálých aktiv v uvažovaných regionech Ruské federace.
Rozhodnutí. Přiřaďte hodnocení prvku Y a faktoru X.
Seřaďme data podle X.
V řadě Y, napravo od 3, je 7 řádků větších než 3, proto z 3 vznikne výraz 7 v P.
Napravo od 1 je 8 řad větších než 1 (to jsou 2, 4, 6, 9, 5, 10, 7, 8), tzn. P bude zahrnovat 8 a tak dále. Výsledkem je, že P = 37 a pomocí vzorců máme:
| X | Y | pořadí X, dx | hodnost Y, d y | P | Q |
| 18.4 | 5.57 | 1 | 3 | 7 | 2 |
| 20.6 | 2.88 | 2 | 1 | 8 | 0 |
| 21.5 | 4.12 | 3 | 2 | 7 | 0 |
| 35.7 | 7.24 | 4 | 4 | 6 | 0 |
| 37.1 | 9.67 | 5 | 6 | 4 | 1 |
| 39.8 | 10.48 | 6 | 9 | 1 | 3 |
| 51.1 | 8.58 | 7 | 5 | 3 | 0 |
| 54.4 | 14.79 | 8 | 10 | 0 | 2 |
| 64.6 | 10.22 | 9 | 7 | 1 | 0 |
| 90.6 | 10.45 | 10 | 8 | 0 | 0 |
| 37 | 8 |
Zjednodušené vzorce:

kde n je velikost vzorku; z kp je kritický bod oboustranné kritické oblasti, který se zjistí z tabulky Laplaceovy funkce pomocí rovnosti Ф(z kp)=(1-α)/2.
Pokud |τ|< T kp - нет оснований отвергнуть нулевую гипотезу. Ранговая корреляционная связь между качественными признаками незначима. Если |τ| >T kp - nulová hypotéza se zamítá. Mezi kvalitativními znaky existuje významná korelace pořadí.
Najdeme kritický bod z kp
Ф(z kp) = (1-α)/2 = (1 - 0,05)/2 = 0,475
Pojďme najít kritický bod:

Protože τ > T kp - zamítáme nulovou hypotézu; korelace pořadí mezi skóre ve dvou testech je významná.
Příklad. Podle objemu provedených stavebních a instalačních prací sám za sebe, a počet zaměstnanců v 10 stavebních firmách v jednom z měst Ruské federace určete vztah mezi těmito znaky pomocí Kendelova koeficientu.
Rozhodnutí najít pomocí kalkulačky.
Přiřaďte hodnocení prvku Y a faktoru X.
Uspořádejme objekty tak, aby jejich pořadí v X představovalo přirozená čísla. Protože hodnocení přiřazená každému páru této série jsou kladná, hodnoty „+1“ zahrnuté v P budou generovány pouze těmi páry, jejichž pořadí v Y tvoří přímé pořadí.
Lze je snadno vypočítat postupným porovnáváním pořadí každého objektu v řadě Y s ocelovými.
Kendallův koeficient.
V obecném případě se výpočet τ (přesněji P nebo Q), a to i pro N v řádu 10, ukazuje jako těžkopádný. Pojďme si ukázat, jak zjednodušit výpočty. 
nebo 
Rozhodnutí.
Seřaďme data podle X.
V řadě Y je napravo od 2 8 řádků větších než 2, takže z 2 vznikne výraz 8 v P.
Napravo od 4 je 6 řad větších než 4 (jedná se o 7, 5, 6, 8, 9, 10), tzn. P bude zahrnovat 6 a tak dále. Výsledkem je, že P = 29 a pomocí vzorců máme:
| X | Y | pořadí X, dx | hodnost Y, d y | P | Q |
| 38 | 292 | 1 | 2 | 8 | 1 |
| 50 | 302 | 2 | 4 | 6 | 2 |
| 52 | 366 | 3 | 7 | 3 | 4 |
| 54 | 312 | 4 | 5 | 4 | 2 |
| 59 | 359 | 5 | 6 | 3 | 2 |
| 61 | 398 | 6 | 8 | 2 | 2 |
| 66 | 401 | 7 | 9 | 1 | 2 |
| 70 | 298 | 8 | 3 | 1 | 1 |
| 71 | 283 | 9 | 1 | 1 | 0 |
| 73 | 413 | 10 | 10 | 0 | 0 |
| 29 | 16 |

Zjednodušené vzorce:


Abychom mohli otestovat nulovou hypotézu na hladině významnosti α, že Kendallův obecný korelační koeficient pořadí je roven nule pod konkurenční hypotézou Н 1: τ ≠ 0, je nutné vypočítat kritický bod:

kde n je velikost vzorku; z kp je kritický bod oboustranné kritické oblasti, který se zjistí z tabulky Laplaceovy funkce pomocí rovnosti Ф(z kp)=(1 - α)/2.
Pokud |τ| T kp - nulová hypotéza se zamítá. Mezi kvalitativními znaky existuje významná korelace pořadí.
Najdeme kritický bod z kp
Ф(z kp) = (1 - α)/2 = (1 - 0,05)/2 = 0,475
Podle Laplaceovy tabulky zjistíme z kp = 1,96
Pojďme najít kritický bod:

Od t
 MNP pro blbce: jak přejít k jinému mobilnímu operátorovi bez změny čísla
MNP pro blbce: jak přejít k jinému mobilnímu operátorovi bez změny čísla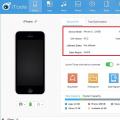 Jak změnit jazyk v iTools Jak si vybrat ruský jazyk na itools
Jak změnit jazyk v iTools Jak si vybrat ruský jazyk na itools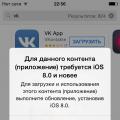 Jaké aplikace přicházejí s ios 7
Jaké aplikace přicházejí s ios 7