ค่าศูนย์ของฟังก์ชันตามกำหนดการ ฟังก์ชันศูนย์ กฎฟังก์ชันศูนย์

การทำงานเป็นหนึ่งในแนวคิดทางคณิตศาสตร์ที่สำคัญที่สุด ฟังก์ชัน - การพึ่งพาตัวแปร ที่จากตัวแปร x, ถ้าแต่ละค่า Xตรงกับค่าเดียว ที่. ตัวแปร Xเรียกว่าตัวแปรอิสระหรืออาร์กิวเมนต์ ตัวแปร ที่เรียกว่าตัวแปรตาม ค่าทั้งหมดของตัวแปรอิสระ (variable x) สร้างโดเมนของฟังก์ชัน ค่าทั้งหมดที่ตัวแปรตามใช้ (variable y) สร้างช่วงของฟังก์ชัน

กราฟฟังก์ชันพวกเขาเรียกชุดของจุดทั้งหมดของระนาบพิกัดซึ่ง abscissas ซึ่งเท่ากับค่าของการโต้แย้งและพิกัดเท่ากับค่าที่สอดคล้องกันของฟังก์ชันนั่นคือค่าของ ตัวแปรถูกพล็อตตามแกน abscissa xและค่าของตัวแปรจะถูกพล็อตตามแกน y y. คุณต้องทราบคุณสมบัติของฟังก์ชันก่อนจึงจะเขียนฟังก์ชันได้ คุณสมบัติหลักของฟังก์ชั่นจะกล่าวถึงด้านล่าง!

ในการพล็อตกราฟฟังก์ชัน เราแนะนำให้ใช้โปรแกรมของเรา - Graphing Functions Online หากคุณมีคำถามใดๆ ในขณะที่ศึกษาเนื้อหาในหน้านี้ คุณสามารถถามพวกเขาได้ตลอดเวลาในฟอรัมของเรา นอกจากนี้ ในฟอรัมนี้ คุณยังจะได้รับความช่วยเหลือในการแก้ปัญหาในวิชาคณิตศาสตร์ เคมี เรขาคณิต ทฤษฎีความน่าจะเป็น และวิชาอื่นๆ อีกมากมาย!

คุณสมบัติพื้นฐานของฟังก์ชัน

1) ขอบเขตฟังก์ชันและช่วงฟังก์ชัน.

ขอบเขตของฟังก์ชันคือชุดของค่าที่ถูกต้องทั้งหมดของอาร์กิวเมนต์ x(ตัวแปร x) ซึ่งฟังก์ชัน y = ฉ(x)กำหนดไว้
พิสัยของฟังก์ชันคือเซตของค่าจริงทั้งหมด yที่ฟังก์ชันยอมรับ

ในวิชาคณิตศาสตร์เบื้องต้น ฟังก์ชันจะศึกษาเฉพาะเซตของจำนวนจริงเท่านั้น

2) ฟังก์ชันศูนย์.

ศูนย์ของฟังก์ชันคือค่าของอาร์กิวเมนต์ที่ค่าของฟังก์ชันเท่ากับศูนย์

3) ช่วงเวลาของความคงตัวของเครื่องหมายของฟังก์ชัน.

ช่วงเครื่องหมายคงที่ของฟังก์ชันคือชุดของค่าอาร์กิวเมนต์ที่ค่าฟังก์ชันเป็นค่าบวกหรือค่าลบเท่านั้น

4) ความน่าเบื่อของฟังก์ชัน.

ฟังก์ชันที่เพิ่มขึ้น (ในช่วงเวลาหนึ่ง) คือฟังก์ชันที่ค่าอาร์กิวเมนต์ที่มากขึ้นจากช่วงเวลานี้สอดคล้องกับค่าที่มากขึ้นของฟังก์ชัน

ลดฟังก์ชัน (ในบางช่วงเวลา) - ฟังก์ชันที่ค่าอาร์กิวเมนต์ที่มากขึ้นจากช่วงเวลานี้สอดคล้องกับค่าที่น้อยกว่าของฟังก์ชัน

5) ฟังก์ชันคู่ (คี่).

ฟังก์ชันคู่คือฟังก์ชันที่โดเมนของคำจำกัดความมีความสมมาตรเมื่อเทียบกับแหล่งกำเนิดและสำหรับใดๆ Xจากขอบเขตของคำจำกัดความความเท่าเทียมกัน ฉ(-x) = ฉ(x). กราฟของฟังก์ชันคู่มีความสมมาตรเกี่ยวกับแกน y

ฟังก์ชันคี่คือฟังก์ชันที่โดเมนของคำจำกัดความมีความสมมาตรเมื่อเทียบกับแหล่งกำเนิดและสำหรับใดๆ Xจากขอบเขตของคำจำกัดความความเท่าเทียมกัน ฉ(-x) = - ฉ(x .)). กราฟของฟังก์ชันคี่มีความสมมาตรเกี่ยวกับจุดกำเนิด

6) ฟังก์ชั่นที่จำกัดและไม่ จำกัด.

ฟังก์ชันเรียกว่า bounded ถ้ามีจำนวนบวก M เช่นนั้น |f(x)| ≤ M สำหรับค่าทั้งหมดของ x หากไม่มีตัวเลขดังกล่าว แสดงว่าฟังก์ชันนั้นไม่มีขอบเขต

7) ช่วงเวลาของฟังก์ชัน.

ฟังก์ชัน f(x) เป็นคาบถ้ามีจำนวน T ที่ไม่เป็นศูนย์ ดังนั้นสำหรับ x f(x+T) = f(x) จำนวนที่น้อยที่สุดนี้เรียกว่าคาบของฟังก์ชัน ฟังก์ชันตรีโกณมิติทั้งหมดเป็นระยะ (สูตรตรีโกณมิติ).

เมื่อศึกษาคุณสมบัติเหล่านี้ของฟังก์ชันแล้ว คุณจะสามารถสำรวจฟังก์ชันได้อย่างง่ายดาย และใช้คุณสมบัติของฟังก์ชัน คุณจะสามารถพล็อตกราฟของฟังก์ชันได้ ดูเนื้อหาเกี่ยวกับตารางความจริง ตารางสูตรคูณ ตารางธาตุ ตารางอนุพันธ์ และตารางอินทิกรัลด้วย

ฟังก์ชันศูนย์

ศูนย์ฟังก์ชันคืออะไร? จะกำหนดศูนย์ของฟังก์ชันได้อย่างไรในเชิงวิเคราะห์และแบบกราฟิก?

ฟังก์ชันศูนย์คือค่าของอาร์กิวเมนต์ที่ฟังก์ชันมีค่าเท่ากับศูนย์

ในการหาค่าศูนย์ของฟังก์ชันที่กำหนดโดยสูตร y=f(x) เราจำเป็นต้องแก้สมการ f(x)=0

ถ้าสมการไม่มีราก แสดงว่าฟังก์ชันนั้นไม่มีศูนย์

1) ค้นหาศูนย์ของฟังก์ชันเชิงเส้น y=3x+15

ในการหาค่าศูนย์ของฟังก์ชัน เราแก้สมการ 3x+15 =0

ดังนั้นศูนย์ของฟังก์ชันคือ y=3x+15 - x= -5 .

2) ค้นหาศูนย์ของฟังก์ชันกำลังสอง f(x)=x²-7x+12

ในการหาค่าศูนย์ของฟังก์ชัน เราแก้สมการกำลังสอง

รากของมัน x1=3 และ x2=4 เป็นศูนย์ของฟังก์ชันนี้

3) ค้นหาศูนย์ของฟังก์ชัน

เศษส่วนเหมาะสมถ้าตัวส่วนต่างจากศูนย์ ดังนั้น x²-1≠0, x² ≠ 1,x ≠±1 นั่นคือโดเมนของคำจำกัดความของฟังก์ชันนี้ (ODZ)

จากรากของสมการ x²+5x+4=0 x1=-1 x2=-4 มีเพียง x=-4 เท่านั้นที่รวมอยู่ในโดเมนของคำจำกัดความ

ในการหาค่าศูนย์ของฟังก์ชันที่แสดงในรูปกราฟ จำเป็นต้องหาจุดตัดของกราฟของฟังก์ชันด้วยแกน x

หากกราฟไม่ตัดกับแกน Ox แสดงว่าฟังก์ชันไม่มีศูนย์

ฟังก์ชั่นที่กราฟแสดงในรูปมีศูนย์สี่ตัว -

ในพีชคณิต ปัญหาในการหาเลขศูนย์ของฟังก์ชันเกิดขึ้นทั้งแบบอิสระและเมื่อแก้ปัญหาอื่นๆ เช่น เมื่อศึกษาฟังก์ชัน การแก้ปัญหาความไม่เท่าเทียมกัน เป็นต้น

www.algebraclass.ru

กฎฟังก์ชันศูนย์

แนวคิดพื้นฐานและคุณสมบัติของฟังก์ชัน

กฎ (กฎหมาย) ความสอดคล้อง ฟังก์ชันโมโนโทนิก .

ฟังก์ชันที่จำกัดและไม่จำกัด ต่อเนื่องและ

การทำงานไม่ต่อเนื่อง . ฟังก์ชันคู่และคี่

ฟังก์ชั่นเป็นระยะ ระยะเวลาการทำงาน

ฟังก์ชันศูนย์ . เส้นกำกับ .

ขอบเขตและช่วงของฟังก์ชัน ในวิชาคณิตศาสตร์เบื้องต้น ฟังก์ชันจะศึกษาเฉพาะเซตของจำนวนจริงเท่านั้น R . ซึ่งหมายความว่าอาร์กิวเมนต์ของฟังก์ชันสามารถรับได้เฉพาะค่าจริงที่กำหนดฟังก์ชันเช่น e . นอกจากนี้ยังยอมรับเฉพาะค่าจริงเท่านั้น เยอะ X ค่าที่ถูกต้องทั้งหมดของอาร์กิวเมนต์ xซึ่งฟังก์ชัน y = ฉ (x) ถูกกำหนดให้เรียกว่า ขอบเขตการทำงาน. เยอะ Y มูลค่าที่แท้จริงทั้งหมด yที่ฟังก์ชั่นยอมรับเรียกว่า ช่วงฟังก์ชัน. ตอนนี้เราสามารถให้คำจำกัดความของฟังก์ชันได้แม่นยำยิ่งขึ้น: กฎ (กฎของ) การโต้ตอบระหว่างเซต Xและ Y , โดยที่แต่ละองค์ประกอบจากเซต Xคุณสามารถหาหนึ่งและหนึ่งองค์ประกอบจากชุด Yเรียกว่าฟังก์ชัน .

จากคำจำกัดความนี้ถือว่ามีการพิจารณาฟังก์ชันหาก:

- ขอบเขตของฟังก์ชันถูกกำหนด X ;

— ตั้งค่าช่วงของค่าฟังก์ชันแล้ว Y ;

- กฎ (กฎหมาย) ของการติดต่อกันเป็นที่ทราบกันดีอยู่แล้วว่าสำหรับแต่ละคน

ค่าอาร์กิวเมนต์ สามารถหาค่าฟังก์ชันได้เพียงค่าเดียวเท่านั้น

ข้อกำหนดเฉพาะของฟังก์ชันนี้บังคับ

ฟังก์ชันโมโนโทนิก ถ้าสำหรับสองค่าของอาร์กิวเมนต์ x 1 และ x 2 ของเงื่อนไข x 2 > x 1 ผู้ติดตาม ฉ (x 2) > ฉ (x 1) จากนั้นฟังก์ชัน ฉ (x) ถูกเรียก เพิ่มขึ้น; ถ้ามี x 1 และ x 2 ของเงื่อนไข x 2 > x 1 ผู้ติดตาม ฉ (x 2)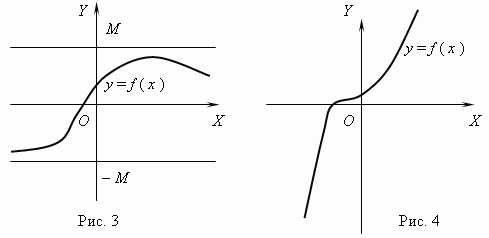

ฟังก์ชันที่แสดงในรูปที่ 3 มีขอบเขตแต่ไม่ใช่แบบโมโนโทนิก ฟังก์ชันในรูปที่ 4 เป็นเพียงตรงกันข้าม โมโนโทนิกแต่ไม่มีขอบเขต (กรุณาอธิบายสิ่งนี้ด้วย!)

ฟังก์ชั่นต่อเนื่องและไม่ต่อเนื่อง การทำงาน y = ฉ (x) ถูกเรียก ต่อเนื่อง ณ จุดนั้น x = เอ, ถ้า:

1) ฟังก์ชั่นถูกกำหนดไว้สำหรับ x = เอ, กล่าวคือ อี ฉ (เอ) มีอยู่;

2) มีอยู่ finiteลิมิตลิมิต ฉ (x) ;

หากไม่เป็นไปตามเงื่อนไขเหล่านี้อย่างน้อยหนึ่งข้อ ฟังก์ชันจะเรียกว่า ไม่ต่อเนื่องณ จุดนั้น x = เอ .

ถ้าฟังก์ชันต่อเนื่องใน ทั้งหมด จุดของโดเมนของคำจำกัดความแล้วจึงเรียกว่า ฟังก์ชันต่อเนื่อง.

ฟังก์ชันคู่และคี่ ถ้าสำหรับ ใด ๆ xจากขอบเขตของการกำหนดฟังก์ชันเกิดขึ้น: ฉ (— x) = ฉ (x) จากนั้นฟังก์ชันจะเรียกว่า สม่ำเสมอ; ถ้าเป็นเช่นนั้น: ฉ (— x) = — ฉ (x) จากนั้นฟังก์ชันจะเรียกว่า แปลก. กราฟของฟังก์ชันคู่ สมมาตรเกี่ยวกับแกน Y(รูปที่ 5) กราฟของฟังก์ชันคี่ ซิม เมตริกเกี่ยวกับแหล่งกำเนิด(รูปที่ 6)

ฟังก์ชั่นเป็นระยะ การทำงาน ฉ (x) — วารสารถ้ามี ไม่ใช่ศูนย์ตัวเลข ตู่เพื่ออะไร ใด ๆ xจากขอบเขตของการกำหนดฟังก์ชันเกิดขึ้น: ฉ (x + ตู่) = ฉ (x). เช่น น้อยที่สุดเบอร์นี้เรียกว่า ระยะเวลาการทำงาน. ฟังก์ชันตรีโกณมิติทั้งหมดเป็นระยะ

ตัวอย่างที่ 1 พิสูจน์ว่าบาป xมีระยะที่ 2

วิธีแก้ปัญหา เรารู้ว่าบาป ( x + 2 น) = บาป x, ที่ไหน น= 0, ± 1, ± 2, …

ดังนั้น บวก 2 นอาร์กิวเมนต์ไซน์

เปลี่ยนค่า e . มีเบอร์นี้อีกมั้ยคะ

มาแสร้งทำเป็นว่า พี- ตัวเลขดังกล่าวเช่น e. ความเท่าเทียมกัน:

ใช้ได้กับค่าใด ๆ x. แต่แล้วก็มี

สถานที่และที่ x= / 2 คือ อี

บาป(/2 + พี) = บาป / 2 = 1.

แต่ตามสูตรการลดบาป (/ 2 + พี) = cos พี. แล้ว

มันตามมาจากความเท่าเทียมกันสองประการสุดท้ายที่cos พี= 1 แต่เรา

เรารู้ว่านี่เป็นความจริงสำหรับ .เท่านั้น พี = 2 น. ตั้งแต่เล็กที่สุด

จำนวนที่ไม่ใช่ศูนย์จาก2 นคือ 2 แล้วตัวเลขนี้

และมีช่วงเวลาบาป x. ได้รับการพิสูจน์ในทำนองเดียวกันว่า 2

เป็นคาบสำหรับ cos x .

พิสูจน์ว่าฟังก์ชัน tan xและแมว xมีช่วงเวลา

ตัวอย่างที่ 2 คาบของฟังก์ชัน sin 2 คือจำนวนใด x ?

วิธีแก้ไข พิจารณาบาป2 x= บาป (2 x + 2 น) = บาป [ 2 ( x + น) ] .

เราเห็นว่าการเพิ่ม นในการโต้แย้ง x,ไม่เปลี่ยน

ค่าฟังก์ชัน จำนวนที่ไม่ใช่ศูนย์ที่น้อยที่สุด

จาก นคือ ดังนั้นนี่คือช่วงเวลาบาป 2 x .

ฟังก์ชัน null ค่าของอาร์กิวเมนต์ที่ฟังก์ชันเท่ากับ 0 เรียกว่า ศูนย์ ( รูท) ฟังก์ชั่น. ฟังก์ชันสามารถมีศูนย์ได้หลายตัว ตัวอย่างเช่น ฟังก์ชัน y = x (x + 1) (x- 3) มีสามศูนย์: x = 0, x = — 1, x= 3 ทางเรขาคณิต ฟังก์ชัน null – คือ abscissa ของจุดตัดของกราฟของฟังก์ชันกับแกน X .

รูปที่ 7 แสดงกราฟของฟังก์ชันที่มีศูนย์: x = เอ , x = ขและ x = ค .

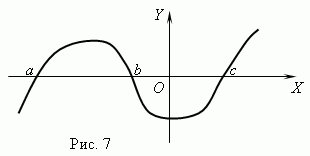
เส้นกำกับ ถ้ากราฟของฟังก์ชันเข้าใกล้เส้นตรงเส้นหนึ่งอย่างไม่มีกำหนดในขณะที่มันเคลื่อนออกจากจุดกำเนิด เส้นตรงนี้จะถูกเรียกว่า เส้นกำกับ.

หัวข้อที่ 6 "วิธีการของช่วงเวลา"

ถ้า f (x) f (x 0) สำหรับ x x 0 ฟังก์ชัน f (x) จะถูกเรียก ต่อเนื่องที่ x 0.

ถ้าฟังก์ชันต่อเนื่องทุกจุดของช่วง I ฟังก์ชันนั้นจะเรียกว่า ต่อเนื่องกันเป็นระยะฉัน (ช่วงที่ฉันเรียกว่า ช่วงเวลาความต่อเนื่องของฟังก์ชัน). กราฟของฟังก์ชันในช่วงเวลานี้เป็นเส้นต่อเนื่อง กล่าวกันว่า "วาดโดยไม่ต้องยกดินสอออกจากกระดาษ"

คุณสมบัติของฟังก์ชันต่อเนื่อง

หากบนช่วง (a ; b) ฟังก์ชัน f ต่อเนื่องและไม่หายไป ฟังก์ชันจะคงค่าคงที่ไว้ในช่วงเวลานี้

วิธีการแก้อสมการด้วยตัวแปรเดียวขึ้นอยู่กับคุณสมบัตินี้ - วิธีการของช่วงเวลา ปล่อยให้ฟังก์ชัน f(x) ต่อเนื่องกันบนช่วง I และหายไปในจุดจำนวนจำกัดในช่วงเวลานี้ โดยคุณสมบัติของฟังก์ชันต่อเนื่อง จุดเหล่านี้แบ่ง I เป็นช่วงๆ โดยแต่ละจุดฟังก์ชันต่อเนื่อง f(x) c ป้องกันเครื่องหมายคงที่ ในการพิจารณาเครื่องหมายนี้ การคำนวณค่าของฟังก์ชัน f(x) ที่จุดใดจุดหนึ่งจากแต่ละช่วงเวลานั้นก็เพียงพอแล้ว จากสิ่งนี้ เราได้รับอัลกอริทึมต่อไปนี้สำหรับการแก้ความไม่เท่าเทียมกันโดยวิธีช่วงเวลา

วิธีช่วงเวลาสำหรับความไม่เท่าเทียมกันของรูปแบบ

ค้นหาโดเมนของฟังก์ชัน f(x) ;

ค้นหาศูนย์ของฟังก์ชัน f(x) ;

วาดโดเมนของคำจำกัดความและศูนย์ของฟังก์ชันบนเส้นจำนวน ค่าศูนย์ของฟังก์ชันจะแบ่งโดเมนของคำจำกัดความออกเป็นช่วงๆ ซึ่งแต่ละฟังก์ชันจะมีเครื่องหมายคงที่

ค้นหาสัญญาณของฟังก์ชันในช่วงเวลาที่ได้รับโดยการคำนวณค่าของฟังก์ชันที่จุดใดจุดหนึ่งจากแต่ละช่วง

เขียนคำตอบ

วิธีช่วงเวลา ระดับกลาง.

คุณต้องการทดสอบจุดแข็งของคุณและค้นหาผลลัพธ์ว่าคุณพร้อมสำหรับการสอบ Unified State หรือ OGE แค่ไหน?

ฟังก์ชันเชิงเส้น

ฟังก์ชันของแบบฟอร์มเรียกว่าเชิงเส้น ลองใช้ฟังก์ชันเป็นตัวอย่าง เป็นบวกที่ 3″> และลบที่ จุดคือศูนย์ของฟังก์ชัน () ให้แสดงสัญญาณของฟังก์ชันนี้บนแกนจริง:

เราบอกว่า "ฟังก์ชันเปลี่ยนเครื่องหมายเมื่อผ่านจุด"

จะเห็นได้ว่าสัญญาณของฟังก์ชันสอดคล้องกับตำแหน่งของกราฟของฟังก์ชัน หากกราฟอยู่เหนือแกน เครื่องหมายจะเป็น " " หากอยู่ด้านล่าง " "

หากเราสรุปกฎผลลัพธ์ให้เป็นฟังก์ชันเชิงเส้นตามอำเภอใจ เราจะได้อัลกอริทึมต่อไปนี้:

เราพบศูนย์ของฟังก์ชัน

เราทำเครื่องหมายบนแกนตัวเลข

เรากำหนดเครื่องหมายของฟังก์ชันที่ด้านตรงข้ามของศูนย์

ฟังก์ชันกำลังสอง

ฉันหวังว่าคุณจะจำได้ไหมว่าอสมการกำลังสองได้รับการแก้ไขอย่างไร ถ้าไม่อ่านหัวข้อ "อสมการกำลังสอง" ผมขอเตือนคุณถึงรูปแบบทั่วไปของฟังก์ชันกำลังสอง:

ทีนี้ มาจำไว้ว่าสัญญาณของฟังก์ชันกำลังสองคืออะไร กราฟของมันคือพาราโบลา และฟังก์ชันใช้เครื่องหมาย " " สำหรับตำแหน่งที่พาราโบลาอยู่เหนือแกน และ " " - หากพาราโบลาอยู่ต่ำกว่าแกน:

หากฟังก์ชันมีศูนย์ (ค่าที่) พาราโบลาตัดกับแกนที่จุดสองจุด - รากของสมการกำลังสองที่สอดคล้องกัน ดังนั้น แกนจะถูกแบ่งออกเป็นสามช่วง และสัญญาณของฟังก์ชันจะเปลี่ยนสลับกันเมื่อผ่านแต่ละรูต

เป็นไปได้ไหมที่จะกำหนดสัญญาณโดยไม่วาดพาราโบลาในแต่ละครั้ง?

จำไว้ว่าจตุรัสไตรนามสามารถแยกตัวประกอบได้:

สังเกตรากบนแกน:

เราจำได้ว่าเครื่องหมายของฟังก์ชันสามารถเปลี่ยนแปลงได้เมื่อผ่านรูทเท่านั้น เราใช้ข้อเท็จจริงนี้: สำหรับแต่ละช่วงสามช่วงที่แกนถูกหารด้วยราก มันก็เพียงพอแล้วที่จะกำหนดเครื่องหมายของฟังก์ชันที่จุดที่เลือกโดยพลการเพียงจุดเดียว ที่จุดอื่นๆ ของช่วงเวลา เครื่องหมายจะเป็น เดียวกัน.

ในตัวอย่างของเรา: สำหรับ 3″> นิพจน์ทั้งสองในวงเล็บเป็นค่าบวก (เราแทนที่ ตัวอย่างเช่น: 0″>) เราใส่เครื่องหมาย "" บนแกน:

ถ้า (เช่น แทนค่า) วงเล็บทั้งสองเป็นค่าลบ ผลคูณจะเป็นค่าบวก:

นั่นแหละค่ะ วิธีช่วงเวลา: เมื่อทราบสัญญาณของปัจจัยในแต่ละช่วงเวลา เราจะกำหนดสัญญาณของผลิตภัณฑ์ทั้งหมด

ให้เราพิจารณากรณีที่ฟังก์ชันไม่มีศูนย์หรือมีเพียงตัวเดียว

ถ้าไม่มีก็ไม่มีราก ซึ่งหมายความว่าจะไม่มี "ทางผ่านรูท" ซึ่งหมายความว่าฟังก์ชันบนแกนตัวเลขทั้งหมดใช้เพียงเครื่องหมายเดียว กำหนดได้ง่ายโดยการแทนค่าลงในฟังก์ชัน

หากมีเพียงรูทเดียว พาราโบลาจะสัมผัสแกน ดังนั้นเครื่องหมายของฟังก์ชันจะไม่เปลี่ยนแปลงเมื่อผ่านรูท กฎสำหรับสถานการณ์ดังกล่าวคืออะไร?

หากเราแยกตัวประกอบของฟังก์ชันดังกล่าว เราจะได้ตัวประกอบที่เหมือนกันสองประการ:

และนิพจน์กำลังสองใดๆ ก็ไม่เป็นลบ! ดังนั้นเครื่องหมายของฟังก์ชันจึงไม่เปลี่ยนแปลง ในกรณีเช่นนี้ เราจะเลือกรูท เมื่อผ่านไปโดยที่เครื่องหมายไม่เปลี่ยน ให้วงกลมด้วยสี่เหลี่ยม:

รากดังกล่าวจะเรียกว่า หลายรายการ.

วิธีการของช่วงเวลาในความไม่เท่าเทียมกัน

ตอนนี้อสมการกำลังสองสามารถแก้ไขได้โดยไม่ต้องวาดพาราโบลา แค่วางเครื่องหมายของฟังก์ชันกำลังสองบนแกนแล้วเลือกช่วงเวลาโดยขึ้นอยู่กับเครื่องหมายอสมการก็เพียงพอแล้ว ตัวอย่างเช่น:

เราวัดรากบนแกนและจัดเรียงสัญญาณ:

เราต้องการส่วนของแกนที่มีเครื่องหมาย ""; เนื่องจากความไม่เท่าเทียมกันไม่เข้มงวด รากเองก็รวมอยู่ในการแก้ปัญหาด้วย:

ตอนนี้ให้พิจารณาอสมการตรรกยะ - อสมการ ซึ่งทั้งสองส่วนเป็นนิพจน์ตรรกยะ (ดู "สมการตรรกยะ")

ตัวอย่าง:

ปัจจัยทั้งหมดยกเว้นหนึ่ง - - นี่คือ "เชิงเส้น" นั่นคือมีตัวแปรในระดับแรกเท่านั้น เราต้องการตัวประกอบเชิงเส้นตรงดังกล่าวเพื่อใช้วิธีช่วงเวลา - เครื่องหมายจะเปลี่ยนเมื่อผ่านรากของพวกมัน แต่ตัวคูณนั้นไม่มีรากเลย ซึ่งหมายความว่ามันเป็นบวกเสมอ (ตรวจสอบด้วยตัวคุณเอง) ดังนั้นจึงไม่ส่งผลต่อสัญญาณของความไม่เท่าเทียมกันทั้งหมด ซึ่งหมายความว่าคุณสามารถแบ่งด้านซ้ายและด้านขวาของอสมการออกได้ และกำจัดมันออกไป:

ตอนนี้ทุกอย่างเหมือนเดิมกับความไม่เท่าเทียมกันกำลังสอง: เรากำหนดว่าปัจจัยแต่ละอย่างหายไป ณ จุดใด ทำเครื่องหมายจุดเหล่านี้บนแกนและจัดเรียงสัญญาณ ฉันดึงความสนใจของคุณไปที่ข้อเท็จจริงที่สำคัญมาก:

ในกรณีของจำนวนคู่ เราดำเนินการในลักษณะเดียวกับก่อนหน้านี้: เราวงกลมจุดด้วยสี่เหลี่ยมจัตุรัสและไม่เปลี่ยนเครื่องหมายเมื่อผ่านรูท แต่ในกรณีของเลขคี่ กฎนี้ไม่สำเร็จ: เครื่องหมายจะยังคงเปลี่ยนเมื่อผ่านรูท ดังนั้นเราจึงไม่ทำอะไรเพิ่มเติมกับรูทดังกล่าว ราวกับว่าไม่ใช่จำนวนของเรา กฎข้างต้นใช้กับพลังเลขคู่และเลขคี่ทั้งหมด

เราเขียนอะไรในคำตอบ?

หากเกิดการสลับกันของสัญญาณ คุณต้องระวังให้มาก เพราะหากขาดความไม่เท่าเทียมกันอย่างเข้มงวด คำตอบควรประกอบด้วย คะแนนเต็ม. แต่บางคนมักยืนอยู่คนเดียว กล่าวคือ ไม่เข้าไปในบริเวณที่มีร่มเงา ในกรณีนี้ เราเพิ่มลงในการตอบสนองเป็นจุดแยก (ในวงเล็บปีกกา):

ตัวอย่าง (ตัดสินใจด้วยตัวเอง):

คำตอบ:

1. ถ้าในบรรดาปัจจัยต่างๆ มันง่าย - นี่คือรูตเพราะสามารถแสดงเป็น
   .

โดยจะใช้ค่าศูนย์ ตัวอย่างเช่น สำหรับฟังก์ชันที่กำหนดโดยสูตร

เป็นโมฆะเพราะ

.

ฟังก์ชันศูนย์เรียกอีกอย่างว่า ฟังก์ชั่นราก.

แนวคิดเรื่องเลขศูนย์ของฟังก์ชันสามารถพิจารณาได้สำหรับฟังก์ชันใดๆ ที่มีช่วงเป็นศูนย์หรือองค์ประกอบศูนย์ของโครงสร้างพีชคณิตที่สอดคล้องกัน

สำหรับฟังก์ชันของตัวแปรจริง ศูนย์คือค่าที่กราฟของฟังก์ชันตัดกับแกน x

การหาค่าศูนย์ของฟังก์ชันมักต้องใช้วิธีการทางตัวเลข (เช่น วิธีของนิวตัน วิธีไล่ระดับ)

ปัญหาทางคณิตศาสตร์ที่แก้ไม่ได้อย่างหนึ่งคือการหาค่าศูนย์ของฟังก์ชันซีตารีมันน์

รากพหุนาม

ดูสิ่งนี้ด้วย

วรรณกรรม

มูลนิธิวิกิมีเดีย 2010 .

ดูว่า "Function Zero" ในพจนานุกรมอื่นๆ คืออะไร:

จุดที่ฟังก์ชันที่กำหนด f(z) หายไป; ดังนั้น N.f. f (z) เหมือนกับรากของสมการ f (z) = 0 ตัวอย่างเช่น จุด 0, π, π, 2π, 2π,... เป็นศูนย์ของฟังก์ชัน sinz ค่าศูนย์ของฟังก์ชันการวิเคราะห์ (ดู การวิเคราะห์ ... ...

ฟังก์ชันศูนย์ ฟังก์ชันศูนย์... พจนานุกรมการสะกดคำ

คำนี้มีความหมายอื่น ดูศูนย์ จำเป็นต้องย้ายเนื้อหาของบทความนี้ไปยังบทความ "Function Zero" คุณสามารถช่วยโครงการโดยรวบรวมบทความ หากคุณต้องการหารือเกี่ยวกับความเหมาะสมของการควบรวมกิจการ ให้แทนที่ ... Wikipedia

หรือสตริง C (จากชื่อภาษา C) หรือสตริง ASCIZ (จากชื่อ assembler directive.asciz) เป็นวิธีการแสดงสตริงในภาษาการเขียนโปรแกรมซึ่งใช้อาร์เรย์ของอักขระแทนการแนะนำ ชนิดสตริงพิเศษและส่วนท้าย ... ... Wikipedia

ในทฤษฎีสนามควอนตัม ชื่อที่ยอมรับ (คำสแลง) สำหรับคุณสมบัติของการหายตัวไปของปัจจัยการปรับค่าปกติของค่าคงที่การมีเพศสัมพันธ์ โดยที่ g0 เป็นค่าคงที่การคัปปลิ้งเปล่าจากอันตรกิริยา Lagrangian, phys คัปปลิ้งคงที่โดยปฏิสัมพันธ์ ความเท่าเทียมกัน Z... สารานุกรมทางกายภาพ

การกลายพันธุ์เป็นศูนย์- การกลายพันธุ์เป็นศูนย์, n. อัลลีล * การกลายพันธุ์เป็นโมฆะ n. อัลลีล * การกลายพันธุ์เป็นโมฆะหรือ n. อัลลีลหรือเงียบ การกลายพันธุ์ที่นำไปสู่การสูญเสียการทำงานอย่างสมบูรณ์ในลำดับ DNA ที่เกิดขึ้น ... พันธุศาสตร์ พจนานุกรมสารานุกรม

ข้อความในทฤษฎีความน่าจะเป็นว่าเหตุการณ์ใด ๆ (ที่เรียกว่าเหตุการณ์ตกค้าง) การเกิดขึ้นซึ่งถูกกำหนดโดยองค์ประกอบระยะไกลโดยพลการของลำดับเหตุการณ์สุ่มอิสระหรือตัวแปรสุ่มมี ... ... สารานุกรมคณิตศาสตร์

1) ตัวเลขที่มีคุณสมบัติที่ตัวเลขใดๆ (จริงหรือเชิงซ้อน) ไม่เปลี่ยนแปลงเมื่อเพิ่มเข้าไป มันเขียนแทนด้วยสัญลักษณ์ 0 ผลคูณของจำนวนใด ๆ ของ N. เท่ากับ N.: หากผลคูณของตัวเลขสองตัวเท่ากับ N. แล้วตัวประกอบตัวใดตัวหนึ่ง ... สารานุกรมคณิตศาสตร์

ฟังก์ชันที่กำหนดโดยความสัมพันธ์ระหว่างตัวแปรอิสระที่ไม่ได้รับการแก้ไขในส่วนหลัง ความสัมพันธ์เหล่านี้เป็นวิธีหนึ่งในการนิยามฟังก์ชัน ตัวอย่างเช่น ความสัมพันธ์ x2 + y2 1 = 0 กำหนด N. f. … สารานุกรมแห่งสหภาพโซเวียตผู้ยิ่งใหญ่

ค่าอาร์กิวเมนต์ z ตามที่ ฉ(z) ไปที่ศูนย์ที่เรียกว่า จุดศูนย์, เช่น. ถ้า ฉ(เอ) = 0 แล้ว a - จุดศูนย์.

def. Dot แต่เรียกว่า สั่งซื้อศูนย์น , ถ้า FKP สามารถแสดงในรูปแบบ ฉ(z) = , โดยที่
ฟังก์ชันวิเคราะห์และ
0.

ในกรณีนี้ ในการขยายฟังก์ชันในอนุกรมเทย์เลอร์ (43) ตัวแรก น สัมประสิทธิ์เป็นศูนย์

= =

เป็นต้น กำหนดลำดับของศูนย์สำหรับ
และ (1-cos z) ที่ z = 0

=
=

ศูนย์ลำดับที่ 1

1 - cos z =
=

ศูนย์ลำดับที่ 2

def. Dot z =
เรียกว่า ชี้ไปที่อนันต์และ ศูนย์ฟังก์ชั่น ฉ(z), ถ้า ฉ(
) = 0. ฟังก์ชันดังกล่าวขยายเป็นอนุกรมในกำลังลบ z : ฉ(z) =
. ถ้า แรก น สัมประสิทธิ์เท่ากับศูนย์ แล้วเราก็มาถึง สั่งเป็นศูนย์ น ที่จุดอนันต์: ฉ(z) = z - น
.

จุดเอกพจน์ที่แยกออกมาแบ่งออกเป็น: ก) จุดเอกพจน์ที่ถอดออกได้; ข) เสาสั่งน; ใน) จุดเอกพจน์ที่สำคัญ.

Dot แต่เรียกว่า จุดเอกพจน์ที่ถอดออกได้ฟังก์ชั่น ฉ(z) ถ้า z
เอ ลิม ฉ(z) = จาก -จำนวนจำกัด .

Dot แต่เรียกว่า เสาแห่งคำสั่งน (น 1) คุณสมบัติ ฉ(z) ถ้าฟังก์ชันผกผัน
= 1/ ฉ(z) มีคำสั่งศูนย์ นณ จุดนั้น แต่.ฟังก์ชันดังกล่าวสามารถแสดงเป็น .ได้เสมอ ฉ(z) =
, ที่ไหน
- ฟังก์ชั่นการวิเคราะห์และ
.

Dot แต่เรียกว่า จุดสำคัญฟังก์ชั่น ฉ(z), ถ้า z
เอ ลิม ฉ(z) ไม่ได้อยู่.

ชุด Laurent

พิจารณากรณีของการบรรจบกันของวงแหวน r < | z 0 – เอ| < Rมีศูนย์กลางอยู่ที่จุด แต่สำหรับฟังก์ชั่น ฉ(z). เราแนะนำสองแวดวงใหม่ หลี่ 1 (r) และ หลี่ 2 (R) ใกล้ขอบเขตของวงแหวนด้วยจุด z 0 ระหว่างพวกเขา ให้เราทำส่วนของวงแหวน เชื่อมวงกลมตามขอบของส่วน ผ่านไปยังภูมิภาคที่เชื่อมต่ออย่างเรียบง่าย และใน

สูตรอินทิกรัล Cauchy (39) เราได้สองอินทิกรัลเหนือตัวแปรz

ฉ(z 0) =
+
, (42)

ที่ซึ่งการบูรณาการไปในทิศทางตรงกันข้าม

สำหรับอินทิกรัลโอเวอร์ หลี่ 1 เงื่อนไข | z 0 – เอ | > | z – เอ | และสำหรับอินทิกรัลโอเวอร์ หลี่ 2 สภาพย้อนกลับ | z 0 – เอ | < | z – เอ |. ดังนั้น ตัวประกอบ 1/( z – z 0) ขยายเป็นอนุกรม (a) ในปริพันธ์มากกว่า หลี่ 2 และในอนุกรม (b) ในอินทิกรัลโอเวอร์ หลี่หนึ่ง . เป็นผลให้เราได้รับการสลายตัว ฉ(z) ในบริเวณวงแหวนใน ชุด Laurentในพลังบวกและลบ ( z 0 – เอ)

ฉ(z 0) =
อา น (z 0 – a) น (43)

ที่ไหน อา น =
=
;อา -น =

การขยายตัวในพลังบวก (z 0 - แต่) เรียกว่า ส่วนขวาซีรีย์ Laurent (ซีรีย์เทย์เลอร์) และการขยายอำนาจเชิงลบเรียกว่า ส่วนสำคัญแถวลอเรนต์.

ถ้าอยู่ในวงกลม หลี่ 1 ไม่มีจุดเอกพจน์และฟังก์ชันคือการวิเคราะห์ จากนั้นใน (44) อินทิกรัลแรกเท่ากับศูนย์โดยทฤษฎีบท Cauchy และมีเพียงส่วนที่ถูกต้องเท่านั้นที่ยังคงอยู่ในการขยายตัวของฟังก์ชัน พลังลบในการขยาย (45) ปรากฏเฉพาะเมื่อการวิเคราะห์ถูกละเมิดภายในวงในและใช้เพื่ออธิบายฟังก์ชันใกล้กับจุดเอกพจน์ที่แยกได้

เพื่อสร้างชุด Laurent (45) สำหรับ ฉ(z) สามารถคำนวณสัมประสิทธิ์การขยายตัวตามสูตรทั่วไปหรือใช้การขยายของฟังก์ชันพื้นฐานที่รวมอยู่ใน ฉ(z).

จำนวนเงื่อนไข ( น) ของส่วนหลักของชุด Laurent ขึ้นอยู่กับประเภทของจุดเอกพจน์: จุดเอกพจน์ที่ถอดออกได้ (น = 0) ; จุดเอกพจน์ที่สำคัญ (น
); เสาน-คำสั่งที่(น - เลขท้าย)

และสำหรับ ฉ(z) = จุด z = 0 จุดเอกพจน์ที่ถอดออกได้,เพราะ ไม่มีส่วนหลัก ฉ(z) = (z -
) = 1 -

ข) สำหรับ ฉ(z) = จุด z = 0 - เสาอันดับ 1

ฉ(z) = (z -
) = -

ค) สำหรับ ฉ(z) = อี 1 / zจุด z = 0 - จุดเอกพจน์ที่สำคัญ

ฉ(z) = อี 1 / z =

ถ้า ฉ(z) เป็นการวิเคราะห์ในโดเมน ดียกเว้น มจุดเอกพจน์แยก และ | z 1 | < |z 2 | < . . . < |z ม| จากนั้นเมื่อขยายฟังก์ชันเป็นกำลัง zเครื่องบินทั้งหมดแบ่งออกเป็น ม+ 1 วง | z ฉัน | < | z | < | z ฉัน+1 | และแหวนรุ่น Laurent ก็มีรูปแบบแตกต่างกันไปตามแต่ละวง เมื่อขยายอำนาจ ( z – z ฉัน ) พื้นที่บรรจบกันของชุด Laurent คือวงกลม | z – z ฉัน | < r, ที่ไหน r คือระยะทางถึงจุดเอกพจน์ที่ใกล้ที่สุด

เป็นต้น ขยายฟังก์ชัน ฉ(z) =ในซีรีส์ของ Laurent ในอำนาจ zและ ( z - 1).

สารละลาย. เราแสดงฟังก์ชันในรูปแบบ ฉ(z) = - z 2 . เราใช้สูตรสำหรับผลรวมของความก้าวหน้าทางเรขาคณิต
. ในวงกลม |z|< 1 ряд сходится и ฉ(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , เช่น. การสลายตัวมีเพียง ถูกต้องส่วนหนึ่ง. ย้ายไปยังบริเวณรอบนอกของวงกลม |z| > 1 . เราแสดงฟังก์ชันในรูปแบบ
โดยที่ 1/| z| < 1, и получим разложение ฉ(z) = z
=z + 1 +

เพราะ , การขยายฟังก์ชันในอำนาจ ( z - 1) ดูเหมือน ฉ(z) = (z - 1) -1 + 2 + (z - 1) สำหรับทุกคน
1.

เป็นต้น ขยายฟังก์ชันในซีรีส์ Laurent ฉ(z) =
: ก) หน่วยเป็นองศา zเป็นวงกลม | z| < 1; b) по степеням z แหวน 1< |z| < 3 ; c) по степеням (z – 2).การตัดสินใจ. มาแยกฟังก์ชันออกเป็นเศษส่วนอย่างง่ายกัน
= =+=
. จากเงื่อนไข z =1
อา = -1/2 , z =3
บี = ½.

แต่) ฉ(z) = ½ [
] = ½ [
-(1/3)
] เมื่อ | z|< 1.

ข) ฉ(z) = - ½ [
+
] = - (
) ที่ 1< |z| < 3.

จาก) ฉ(z) = ½ [
]= - ½ [
] =

= - ½ = -
, สำหรับ |2 - z| < 1

เป็นวงกลมรัศมี 1 จุดศูนย์กลาง z = 2 .

ในบางกรณี อนุกรมกำลังสามารถลดลงเป็นชุดของความก้าวหน้าทางเรขาคณิต จากนั้นจึงง่ายต่อการกำหนดพื้นที่ของการบรรจบกัน

เป็นต้น สำรวจการบรรจบกันของซีรีส์

. . . + + + + 1 + () + () 2 + () 3 + . . .

สารละลาย. เป็นผลรวมของความก้าวหน้าทางเรขาคณิตสองอย่างกับ q 1 = , q 2 = () . จากเงื่อนไขของการบรรจบกันของมันมีดังนี้ < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

ศูนย์ฟังก์ชันคืออะไร? คำตอบนั้นค่อนข้างง่าย - นี่เป็นศัพท์ทางคณิตศาสตร์ ซึ่งหมายถึงโดเมนของฟังก์ชันที่กำหนด โดยมีค่าเป็นศูนย์ ศูนย์ฟังก์ชันเรียกอีกอย่างว่าศูนย์ฟังก์ชัน วิธีที่ง่ายที่สุดในการอธิบายว่าศูนย์ฟังก์ชันคืออะไรโดยใช้ตัวอย่างง่ายๆ

ตัวอย่าง

พิจารณาสมการอย่างง่าย y=x+3 เนื่องจากศูนย์ของฟังก์ชันคือค่าของอาร์กิวเมนต์ที่ y กลายเป็นศูนย์ เราจึงแทน 0 ทางด้านซ้ายของสมการ:

ในกรณีนี้ -3 เป็นศูนย์ที่ต้องการ สำหรับฟังก์ชันที่กำหนด จะมีรากของสมการเพียงรากเดียว แต่ก็ไม่เสมอไป

ลองพิจารณาตัวอย่างอื่น:

แทนที่ 0 ทางด้านซ้ายของสมการดังตัวอย่างก่อนหน้า:

แน่นอน ในกรณีนี้ จะมีฟังก์ชันเป็นศูนย์สองตัว: x=3 และ x=-3 ถ้าสมการมีอาร์กิวเมนต์ของดีกรีที่สาม ก็จะมีศูนย์สามตัว เราสามารถสรุปง่ายๆ ได้ว่าจำนวนรากของพหุนามสอดคล้องกับระดับสูงสุดของอาร์กิวเมนต์ในสมการ อย่างไรก็ตาม ฟังก์ชันหลายอย่าง เช่น y=x 3 เมื่อแรกเห็น ขัดแย้งกับคำสั่งนี้ ตรรกะและสามัญสำนึกแนะนำว่าฟังก์ชันนี้มีศูนย์เพียงตัวเดียว - ที่จุด x=0 แต่อันที่จริงมีสามราก พวกมันทั้งหมดตรงกัน หากคุณแก้สมการในรูปแบบที่ซับซ้อน สิ่งนี้จะชัดเจน x=0 ในกรณีนี้ ค่ารูท ซึ่งค่าหลายหลากเท่ากับ 3 ในตัวอย่างก่อนหน้านี้ ค่าศูนย์ไม่ตรงกัน ดังนั้นจึงมีค่าหลายหลากเท่ากับ 1

อัลกอริธึมคำจำกัดความ

จากตัวอย่างที่นำเสนอ จะทราบวิธีการกำหนดศูนย์ของฟังก์ชันได้อย่างชัดเจน อัลกอริทึมจะเหมือนกันเสมอ:

1. เขียนฟังก์ชัน.
2. แทนที่ y หรือ f(x)=0
3. แก้สมการผลลัพธ์

ความซับซ้อนของรายการสุดท้ายขึ้นอยู่กับระดับของการโต้แย้งของสมการ เมื่อแก้สมการที่มีระดับสูง สิ่งสำคัญอย่างยิ่งคือต้องจำไว้ว่าจำนวนรากของสมการนั้นเท่ากับกำลังสูงสุดของอาร์กิวเมนต์ นี่เป็นเรื่องจริงโดยเฉพาะอย่างยิ่งสำหรับสมการตรีโกณมิติ ซึ่งการหารทั้งสองส่วนด้วยไซน์หรือโคไซน์ทำให้สูญเสียราก

สมการองศาตามอำเภอใจแก้ได้ง่ายที่สุดโดยวิธีของฮอร์เนอร์ ซึ่งพัฒนาขึ้นโดยเฉพาะสำหรับการหาค่าศูนย์ของพหุนามตามอำเภอใจ

ค่าของศูนย์ของฟังก์ชันสามารถเป็นได้ทั้งค่าลบและค่าบวก ค่าจริงหรือค่าที่อยู่ในระนาบเชิงซ้อน ค่าเดียวหรือค่าหลายค่า หรืออาจไม่มีรากของสมการ ตัวอย่างเช่น ฟังก์ชัน y=8 จะไม่กลายเป็นศูนย์สำหรับ x ใดๆ เนื่องจากไม่ได้ขึ้นอยู่กับตัวแปรนี้

สมการ y=x 2 -16 มีสองราก และทั้งคู่อยู่ในระนาบเชิงซ้อน: x 1 =4i, x 2 =-4i

ข้อผิดพลาดทั่วไป

ข้อผิดพลาดทั่วไปที่เกิดขึ้นโดยเด็กนักเรียนที่ยังไม่ทราบว่าศูนย์ของฟังก์ชันกำลังแทนที่อาร์กิวเมนต์ (x) ด้วยศูนย์และไม่ใช่ค่า (y) ของฟังก์ชัน พวกเขาแทนที่ x = 0 ลงในสมการอย่างมั่นใจและจากสิ่งนี้ หา y แต่นี่เป็นแนวทางที่ผิด

ข้อผิดพลาดอีกประการหนึ่งดังที่ได้กล่าวไปแล้วคือการลดลงโดยไซน์หรือโคไซน์ในสมการตรีโกณมิติ ซึ่งเป็นสาเหตุที่ทำให้ฟังก์ชันศูนย์หนึ่งตัวหรือมากกว่าหายไป นี่ไม่ได้หมายความว่าไม่มีสิ่งใดสามารถลดลงในสมการดังกล่าวได้ แต่จะต้องคำนึงถึงปัจจัยที่ "สูญหาย" เหล่านี้ในการคำนวณเพิ่มเติม

การแสดงกราฟิก

คุณสามารถทำความเข้าใจว่าศูนย์ของฟังก์ชันคืออะไรด้วยความช่วยเหลือของโปรแกรมทางคณิตศาสตร์ เช่น Maple ในนั้น คุณสามารถสร้างกราฟโดยระบุจำนวนจุดที่ต้องการและมาตราส่วนที่ต้องการ จุดที่กราฟตัดผ่านแกน OX คือค่าศูนย์ที่ต้องการ นี่เป็นวิธีที่เร็วที่สุดวิธีหนึ่งในการหารากของพหุนาม โดยเฉพาะอย่างยิ่งถ้าลำดับของมันสูงกว่าลำดับที่สาม ดังนั้นหากจำเป็นต้องคำนวณทางคณิตศาสตร์เป็นประจำ ให้หารากของพหุนามขององศาตามอำเภอใจ สร้างกราฟ Maple หรือโปรแกรมที่คล้ายกันจะขาดไม่ได้ในการดำเนินการและตรวจสอบการคำนวณ

การแสดงทางคณิตศาสตร์ของฟังก์ชันแสดงให้เห็นชัดเจนว่าปริมาณหนึ่งกำหนดมูลค่าของปริมาณอื่นได้อย่างไร ตามเนื้อผ้า ฟังก์ชันตัวเลขจะถือว่าเชื่อมโยงตัวเลขหนึ่งกับอีกจำนวนหนึ่ง ค่าศูนย์ของฟังก์ชันมักจะเรียกว่าค่าของอาร์กิวเมนต์ที่ฟังก์ชันหายไป

การเรียนการสอน

1. ในการหาค่าศูนย์ของฟังก์ชัน คุณต้องถือด้านขวาของฟังก์ชันให้เป็นศูนย์และแก้สมการที่ได้ ลองนึกภาพว่าคุณได้รับฟังก์ชัน f(x)=x-5

2. ในการหาเลขศูนย์ของฟังก์ชันนี้ ให้หาค่าด้านขวาเท่ากับศูนย์: x-5=0

3. การแก้สมการนี้ เราจะได้ว่า x=5 และค่าของอาร์กิวเมนต์นี้จะเป็นศูนย์ของฟังก์ชัน นั่นคือ เมื่อค่าของอาร์กิวเมนต์เท่ากับ 5 ฟังก์ชัน f(x) จะหายไป

อยู่ระหว่างการส่ง ฟังก์ชั่นในวิชาคณิตศาสตร์เข้าใจความสัมพันธ์ระหว่างองค์ประกอบของเซต เพื่อให้ถูกต้องมากขึ้น นี่คือ "กฎ" ตามที่องค์ประกอบทั้งหมดของชุดหนึ่ง (เรียกว่าโดเมนของคำจำกัดความ) ถูกกำหนดองค์ประกอบบางอย่างของชุดอื่น (เรียกว่าโดเมนของค่า)

คุณจะต้องการ

• ความรู้ในการทบทวนพีชคณิตและคณิตศาสตร์

การเรียนการสอน

1. ค่านิยม ฟังก์ชั่นนี่คือพื้นที่บางส่วนที่ฟังก์ชันสามารถรับค่าได้ สมมติว่าช่วง ฟังก์ชั่น f(x)=|x| จาก 0 ถึงอนันต์ ที่จะค้นพบ ความหมาย ฟังก์ชั่นเมื่อถึงจุดหนึ่ง คุณต้องแทนที่อาร์กิวเมนต์ ฟังก์ชั่นเทียบเท่าตัวเลข ผลลัพธ์ที่ได้จะเป็น ความหมายม ฟังก์ชั่น. ให้ฟังก์ชัน f(x)=|x| – 10 + 4x. ค้นพบ ความหมาย ฟังก์ชั่นที่จุด x=-2 แทนที่ตัวเลข -2 แทน x: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16 เช่น ความหมาย ฟังก์ชั่นที่จุด -2 คือ -16

บันทึก!
ก่อนค้นหาค่าของฟังก์ชัน ณ จุดใดจุดหนึ่ง ตรวจสอบให้แน่ใจว่าได้รวมอยู่ในขอบเขตของฟังก์ชันแล้ว

คำแนะนำที่เป็นประโยชน์
ด้วยวิธีการที่คล้ายกัน คุณสามารถค้นหาค่าของฟังก์ชันของอาร์กิวเมนต์หลายตัวได้ ข้อแตกต่างคือแทนที่จะใช้ตัวเลขเดียว คุณจะต้องแทนที่หลายตัว - ตามจำนวนอาร์กิวเมนต์ของฟังก์ชัน

ฟังก์ชันคือความสัมพันธ์ที่กำหนดขึ้นของตัวแปร y จากตัวแปร x นอกจากนี้ ค่าทั้งหมดของ x ซึ่งเรียกว่าอาร์กิวเมนต์ สอดคล้องกับค่าพิเศษของ y - ฟังก์ชัน ในรูปแบบกราฟิก ฟังก์ชันจะแสดงบนระบบพิกัดคาร์ทีเซียนในรูปแบบของกราฟ จุดตัดของกราฟที่มีแกน abscissa ซึ่งมีการพล็อตอาร์กิวเมนต์ x เรียกว่าศูนย์ของฟังก์ชัน การหาค่าศูนย์ที่ถูกต้องเป็นหนึ่งในภารกิจในการค้นหาฟังก์ชันที่กำหนด ในกรณีนี้ ค่าที่ยอมรับได้ทั้งหมดของตัวแปรอิสระ x ซึ่งเป็นโดเมนของนิยามฟังก์ชัน (OOF) จะถูกนำมาพิจารณาด้วย

การเรียนการสอน

1. ศูนย์ของฟังก์ชันคือค่าของอาร์กิวเมนต์ x ซึ่งค่าของฟังก์ชันเป็นศูนย์ อย่างไรก็ตาม เฉพาะอาร์กิวเมนต์ที่รวมอยู่ในโดเมนของคำจำกัดความของฟังก์ชันภายใต้การศึกษาเท่านั้นที่สามารถเป็นศูนย์ได้ นั่นคือในหลาย ๆ ค่าที่ฟังก์ชัน f (x) มีความรู้สึก

2. จดฟังก์ชันที่ให้มาและหาค่าเป็นศูนย์ เช่น f(x) = 2x?+5x+2 = 0 แก้สมการที่ได้และหารากที่แท้จริงของมัน รากของสมการกำลังสองคำนวณด้วยการสนับสนุนการหา discriminant 2x? + 5x + 2 \u003d 0; D \u003d b? -4ac \u003d 5? -4 * 2 * 2 \u003d 9; x1 \u003d (-b +? D) / 2 * a \u003d (-5 + 3) / 2 * 2 \u003d -0.5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2 ดังนั้นในกรณีนี้สอง รากของสมการกำลังสองได้มาซึ่งสอดคล้องกับอาร์กิวเมนต์ของฟังก์ชันเริ่มต้น f(x)

3. ตรวจสอบค่า x ที่ตรวจพบทั้งหมดว่าเป็นของโดเมนคำจำกัดความของฟังก์ชันที่กำหนด ตรวจหา OOF เมื่อต้องการทำเช่นนี้ ให้ตรวจสอบนิพจน์เริ่มต้นสำหรับการมีอยู่ของรากของระดับคู่ของรูปแบบหรือไม่ f (x) สำหรับการมีอยู่ของเศษส่วนในฟังก์ชันที่มีอาร์กิวเมนต์ในตัวส่วน สำหรับการมีอยู่ของลอการิทึมหรือ นิพจน์ตรีโกณมิติ

4. เมื่อพิจารณาฟังก์ชันที่มีนิพจน์ภายใต้รูทของดีกรีคู่ ให้ใช้อาร์กิวเมนต์ x ทั้งหมดในขอบเขตของคำจำกัดความ ค่าที่ไม่เปลี่ยนนิพจน์รูทเป็นจำนวนลบ (ในทางตรงกันข้าม ฟังก์ชันทำ ไม่สมเหตุสมผล) ระบุว่าค่าศูนย์ที่ตรวจพบของฟังก์ชันอยู่ในช่วงค่า x ที่ยอมรับได้หรือไม่

5. ตัวส่วนของเศษส่วนไม่สามารถหายไปได้ ดังนั้นจึงไม่รวมอาร์กิวเมนต์ x ที่นำไปสู่ผลลัพธ์ดังกล่าว สำหรับปริมาณลอการิทึม ควรพิจารณาเฉพาะค่าของอาร์กิวเมนต์ที่นิพจน์นั้นมีค่ามากกว่าศูนย์ ค่าศูนย์ของฟังก์ชันที่เปลี่ยนนิพจน์ย่อยของลอการิทึมเป็นศูนย์หรือค่าลบจะต้องละทิ้งจากผลลัพธ์สุดท้าย

บันทึก!
เมื่อหารากของสมการ รากพิเศษอาจปรากฏขึ้น ง่ายที่จะตรวจสอบสิ่งนี้: เพียงพอที่จะแทนที่ค่าที่ได้รับของอาร์กิวเมนต์ลงในฟังก์ชันแล้วตรวจสอบให้แน่ใจว่าฟังก์ชันหายไป

คำแนะนำที่เป็นประโยชน์
ในบางครั้ง ฟังก์ชันจะไม่แสดงออกอย่างชัดเจนผ่านการโต้แย้ง จึงเป็นเรื่องง่ายที่จะทราบว่าฟังก์ชันคืออะไร ตัวอย่างนี้คือสมการของวงกลม