Ničele funkcije po urniku. Funkcija nič. Pravilo ničelne funkcije

Funkcija je eden najpomembnejših matematičnih konceptov. Funkcija - spremenljiva odvisnost pri iz spremenljivke x, če je vsaka vrednost X se ujema z eno samo vrednostjo pri. spremenljivka X imenujemo neodvisna spremenljivka ali argument. spremenljivka pri imenovana odvisna spremenljivka. Vse vrednosti neodvisne spremenljivke (spremenljivke x) tvorijo domeno funkcije. Vse vrednosti, ki jih prevzame odvisna spremenljivka (spremenljivka y), tvorijo obseg funkcije.

Funkcijski graf imenujejo množico vseh točk koordinatne ravnine, katerih abscise so enake vrednostim argumenta, ordinate pa enake ustreznim vrednostim funkcije, to je vrednostim spremenljivke so narisane vzdolž abscisne osi x, vrednosti spremenljivke pa so izrisane vzdolž osi y y. Za izris funkcije morate poznati lastnosti funkcije. Glavne lastnosti funkcije bodo obravnavane spodaj!

Za izris funkcijskega grafa priporočamo uporabo našega programa - Graphing Functions Online. Če imate med preučevanjem gradiva na tej strani kakršna koli vprašanja, jih lahko vedno postavite na našem forumu. Tudi na forumu vam bodo pomagali pri reševanju nalog iz matematike, kemije, geometrije, teorije verjetnosti in mnogih drugih predmetov!

Osnovne lastnosti funkcij.

1) Obseg funkcije in obseg funkcij.

Obseg funkcije je nabor vseh veljavnih vrednosti argumenta x(spremenljiva x), za katerega je funkcija y = f(x) opredeljeno.
Obseg funkcije je množica vseh realnih vrednosti y da funkcija sprejme.

V osnovni matematiki se funkcije preučujejo samo na množici realnih števil.

2) Funkcijske ničle.

Nič funkcije je vrednost argumenta, pri kateri je vrednost funkcije enaka nič.

3) Intervali predznakovne konstantnosti funkcije.

Intervali konstantnega predznaka funkcije so takšni nizi vrednosti argumentov, na katerih so vrednosti funkcije samo pozitivne ali samo negativne.

4) Monotonost funkcije.

Naraščajoča funkcija (v nekem intervalu) - funkcija, pri kateri večja vrednost argumenta iz tega intervala ustreza večji vrednosti funkcije.

Zmanjšajoča funkcija (v nekem intervalu) - funkcija, pri kateri večji vrednosti argumenta iz tega intervala ustreza manjši vrednosti funkcije.

5) Sode (lihe) funkcije.

Soda funkcija je funkcija, katere področje definicije je simetrično glede na izvor in za katero koli X iz domene definicije enakost f(-x) = f(x). Graf sode funkcije je simetričen glede na os y.

Neparna funkcija je funkcija, katere domena definicije je simetrična glede na izvor in za katero koli X iz domene definicije enakost f(-x) = - f(x). Graf lihe funkcije je simetričen glede na izvor.

6) Omejene in neomejene funkcije.

Funkcija se imenuje omejena, če obstaja pozitivno število M, tako da je |f(x)| ≤ M za vse vrednosti x. Če takšnega števila ni, je funkcija neomejena.

7) Periodičnost funkcije.

Funkcija f(x) je periodična, če obstaja število T, ki ni nič, tako da je za kateri koli x f(x+T) = f(x). To najmanjše število se imenuje obdobje funkcije. Vse trigonometrične funkcije so periodične. (Trigonometrične formule).

Ko preučite te lastnosti funkcije, lahko preprosto raziščete funkcijo in z uporabo lastnosti funkcije lahko narišete graf funkcije. Oglejte si tudi gradivo o tabeli resnice, tabeli množenja, periodnem sistemu, tabeli izpeljank in tabeli integralov.

Funkcijske ničle

Kaj so ničle funkcije? Kako analitično in grafično določiti ničle funkcije?

Funkcijske ničle so vrednosti argumenta, pri katerih je funkcija enaka nič.

Za iskanje ničel funkcije, podane s formulo y=f(x), moramo rešiti enačbo f(x)=0.

Če enačba nima korenin, potem funkcija nima ničel.

1) Poiščite ničle linearne funkcije y=3x+15.

Za iskanje ničel funkcije rešimo enačbo 3x+15 =0.

Torej je nič funkcije y=3x+15 - x= -5.

2) Poiščite ničle kvadratne funkcije f(x)=x²-7x+12.

Za iskanje ničel funkcije rešimo kvadratno enačbo

Njeni koreni x1=3 in x2=4 sta ničli te funkcije.

3) Poiščite ničle funkcije

Ulomek je smiseln, če je imenovalec drugačen od nič. Zato je x²-1≠0, x² ≠ 1,x ≠±1. To je domena definicije te funkcije (ODZ)

Iz korenin enačbe x²+5x+4=0 x1=-1 x2=-4 je v domeno definicije vključen samo x=-4.

Za iskanje ničel funkcije, podane grafično, je treba poiskati presečne točke grafa funkcije z osjo x.

Če graf ne prečka osi Ox, funkcija nima ničel.

funkcija, katere graf je prikazan na sliki, ima štiri ničle -

V algebri se problem iskanja ničel funkcije pojavlja tako kot samostojna naloga kot pri reševanju drugih problemov, na primer pri preučevanju funkcije, reševanju neenakosti itd.

www.algebraclass.ru

Pravilo ničelne funkcije

Osnovni pojmi in lastnosti funkcij

pravilo (zakon) skladnosti. Monotona funkcija .

Omejene in neomejene funkcije. Neprekinjeno in

prekinjena funkcija . Sode in lihe funkcije.

Periodična funkcija. Obdobje delovanja.

Funkcijske ničle . Asimptota .

Obseg in obseg funkcije. V osnovni matematiki se funkcije preučujejo samo na množici realnih števil R . To pomeni, da lahko argument funkcije prevzame le tiste realne vrednosti, za katere je funkcija definirana, tj. sprejema tudi samo prave vrednosti. Veliko X vse veljavne veljavne vrednosti argumenta x, za katerega je funkcija y = f (x) je definiran, imenovan obseg funkcije. Veliko Y vse prave vrednosti y ki ga funkcija sprejme, se pokliče obseg delovanja. Zdaj lahko podamo natančnejšo definicijo funkcije: pravilo (zakon) korespondence med množicami X in Y , s katerim za vsak element iz množice X lahko najdete en in samo en element iz nabora Y, se imenuje funkcija .

Iz te definicije sledi, da se funkcija šteje za dano, če:

- obseg funkcije je nastavljen X ;

— nastavljen je obseg funkcijskih vrednosti Y ;

- pravilo (zakon) korespondence je znano in tako, da za vsako

vrednosti argumentov, je mogoče najti samo eno vrednost funkcije.

Ta zahteva po edinstvenosti funkcije je obvezna.

monotono funkcijo. Če za kateri koli dve vrednosti argumenta x 1 in x 2 pogoja x 2 > x 1 sledi f (x 2) > f (x 1), nato funkcija f (x) je poklican naraščajoče; če za katero x 1 in x 2 pogoja x 2 > x 1 sledi f (x 2)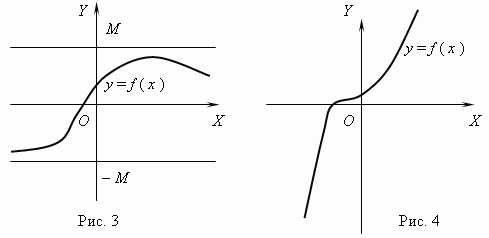

Funkcija, prikazana na sliki 3, je omejena, vendar ne monotona. Funkcija na sliki 4 je ravno nasprotna, monotona, a neomejena. (Prosim, pojasnite to!)

Neprekinjene in prekinjene funkcije. Funkcija y = f (x) je poklican neprekinjeno na točki x = a, če:

1) funkcija je definirana za x = a, t.j. e. f (a) obstaja;

2) obstaja končno meja lim f (x) ;

Če vsaj eden od teh pogojev ni izpolnjen, se funkcija pokliče prekinjeno na točki x = a .

Če je funkcija neprekinjena v vse točke njegovega področja definicije, potem se imenuje neprekinjena funkcija.

Sode in lihe funkcije. Če za kaj x iz obsega definicije funkcije poteka: f (— x) = f (x), potem se funkcija pokliče celo; če se: f (— x) = — f (x), potem se funkcija pokliče Čuden. Graf sode funkcije simetrično glede na os Y(slika 5), ​​graf lihe funkcije Sim metrika o izvoru(slika 6).

Periodična funkcija. Funkcija f (x) — periodičnoče taka obstaja neničštevilko T kaj za kaj x iz obsega definicije funkcije poteka: f (x + T) = f (x). Takšne vsajštevilka je poklicana obdobje delovanja. Vse trigonometrične funkcije so periodične.

PRIMER 1. Dokaži ta greh x ima obdobje 2.

REŠITEV Vemo, da greh ( x + 2 n) = greh x, kje n= 0, ± 1, ± 2, …

Zato dodamo 2 n na sinusni argument

spremeni svojo vrednost e. Ali obstaja še kakšna številka s tem

Pretvarjajmo se P- taka številka, tj. enakost:

velja za katero koli vrednost x. Ampak potem je

mestu in na x= / 2, tj.

greh(/2 + P) = greh / 2 = 1.

Toda po redukcijski formuli sin (/ 2 + P) = cos P. Potem

iz zadnjih dveh enakosti sledi, da cos P= 1, ampak mi

Vemo, da to velja samo za P = 2 n. Od najmanjšega

število, ki ni nič od 2 n je 2, potem je to število

in obstaja obdobje greh x. Podobno se dokazuje, da 2

je obdobje za cos x .

Dokaži, da funkcije tan x in mačka x imeti menstruacijo.

Primer 2. Kakšno število je obdobje funkcije sin 2 x ?

Rešitev. Razmislite o grehu 2 x= greh (2 x + 2 n) = greh [ 2 ( x + n) ] .

Vidimo to dodajanje n na argument x, se ne spremeni

vrednost funkcije. Najmanjše število, ki ni nič

od n je , torej je to obdobje sin 2 x .

Ničele funkcije. Prikliče se vrednost argumenta, za katerega je funkcija enaka 0 nič ( korenske) funkcije. Funkcija ima lahko več ničel. Na primer funkcija y = x (x + 1) (x- 3) ima tri ničle: x = 0, x = — 1, x= 3. Geometrijsko funkcija nič – je abscisa presečišča grafa funkcije z osjo X .

Slika 7 prikazuje graf funkcije z ničlami: x = a , x = b in x = c .

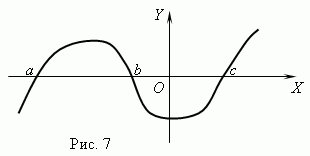
Asimptota. Če se graf funkcije za nedoločen čas približuje določeni ravni črti, ko se ta odmika od izhodišča, se ta ravna črta imenuje asimptota.

Tema 6. "Metoda intervalov".

Če je f (x) f (x 0) za x x 0, se pokliče funkcija f (x). neprekinjeno pri x 0.

Če je funkcija zvezna na vsaki točki nekega intervala I, se imenuje neprekinjeno v intervalu I (interval I se imenuje interval kontinuitete funkcije). Graf funkcije na tem intervalu je neprekinjena črta, za katero pravimo, da je "narisana, ne da bi dvignili svinčnik s papirja."

Lastnost neprekinjenih funkcij.

Če je na intervalu (a ; b) funkcija f neprekinjena in ne izgine, ostane na tem intervalu konstanten predznak.

Metoda reševanja neenakosti z eno spremenljivko temelji na tej lastnosti – metodi intervalov. Naj je funkcija f(x) neprekinjena na intervalu I in se izniči na končnem številu točk v tem intervalu. Z lastnostjo zveznih funkcij te točke delijo I na intervale, v vsakem od katerih neprekinjena funkcija f(x) c varuje konstanten predznak. Za določitev tega predznaka je dovolj izračunati vrednost funkcije f(x) na kateri koli točki iz vsakega takega intervala. Na podlagi tega dobimo naslednji algoritem za reševanje neenakosti po intervalni metodi.

Intervalna metoda za neenakosti obrazca

Poiščite domeno funkcije f(x) ;

Poiščite ničle funkcije f(x) ;

Na številski premici nariši domeno definicije in ničle funkcije. Ničele funkcije delijo njeno področje definicije na intervale, v vsakem od katerih funkcija ohrani konstanten predznak;

Poiščite predznake funkcije v dobljenih intervalih tako, da izračunate vrednost funkcije na kateri koli točki iz vsakega intervala;

Zapišite odgovor.

intervalna metoda. Povprečna raven.

Želite preizkusiti svojo moč in ugotoviti rezultat, kako ste pripravljeni na enotni državni izpit ali OGE?

Linearna funkcija

Funkcija oblike se imenuje linearna. Vzemimo za primer funkcijo. Pozitivna je pri 3″> in negativna pri. Točka je nič funkcije (). Pokažimo znake te funkcije na realni osi:

Pravimo, da "funkcija spremeni predznak, ko gre skozi točko".

Vidimo, da predznaki funkcije ustrezajo položaju grafa funkcije: če je graf nad osjo, je znak “ ”, če je pod njo, “ ”.

Če dobljeno pravilo posplošimo na poljubno linearno funkcijo, dobimo naslednji algoritem:

Najdemo nič funkcije;

Označimo ga na številčni osi;

Določimo predznak funkcije na nasprotnih straneh ničle.

kvadratna funkcija

Upam, da se spomnite, kako se rešujejo kvadratne neenakosti? Če ne, preberite temo "Kvadratne neenakosti". Naj vas spomnim na splošno obliko kvadratne funkcije: .

Zdaj se spomnimo, kakšne znake ima kvadratna funkcija. Njegov graf je parabola, funkcija pa vzame znak " " za tiste, pri katerih je parabola nad osjo, in " " - če je parabola pod osjo:

Če ima funkcija ničle (vrednosti, pri katerih), parabola seka os v dveh točkah - koreninah ustrezne kvadratne enačbe. Tako je os razdeljena na tri intervale, predznaki funkcije pa se pri prehodu skozi vsak koren izmenično spreminjajo.

Ali je mogoče nekako določiti znake, ne da bi vsakič narisali parabolo?

Spomnimo se, da je kvadratni trinom mogoče faktorizirati:

Upoštevajte korenine na osi:

Spomnimo se, da se predznak funkcije lahko spremeni le pri prehodu skozi koren. Uporabljamo to dejstvo: za vsakega od treh intervalov, na katere je os razdeljena s koreninami, je dovolj, da določimo predznak funkcije samo na eni poljubno izbrani točki: na drugih točkah intervala bo predznak enako.

V našem primeru: za 3″> sta oba izraza v oklepaju pozitivna (zamenjamo, na primer: 0″>). Na os postavimo znak "":

No, če sta (na primer nadomestek) oba oklepaja negativna, potem je produkt pozitiven:

To je tisto, kar je intervalna metoda: poznamo predznake faktorjev na vsakem intervalu, določimo predznak celotnega produkta.

Razmislimo tudi o primerih, ko funkcija nima ničel ali pa je le ena.

Če jih ni, potem ni korenin. To pomeni, da ne bo "prehoda skozi koren". To pomeni, da ima funkcija na celotni številski osi samo en predznak. To je enostavno določiti tako, da ga nadomestimo s funkcijo.

Če obstaja samo en koren, se parabola dotika osi, zato se predznak funkcije pri prehodu skozi koren ne spremeni. Kakšno je pravilo za takšne situacije?

Če izvzamemo takšno funkcijo, dobimo dva enaka faktorja:

In vsak izraz na kvadrat ni negativen! Zato se predznak funkcije ne spremeni. V takih primerih bomo izbrali koren, pri prehodu skozi katerega se znak ne spremeni, in ga obkrožili s kvadratom:

Tak koren se bo imenoval večkraten.

Metoda intervalov v neenakostih

Sedaj je mogoče vsako kvadratno neenakost rešiti brez risanja parabole. Dovolj je le, da na os postavimo znake kvadratne funkcije in izberete intervale glede na predznak neenakosti. Na primer:

Izmerimo korenine na osi in razporedimo znake:

Potrebujemo del osi z znakom ""; ker neenakost ni stroga, so v rešitev vključene tudi same korenine:

Zdaj razmislite o racionalni neenakosti - neenakosti, katere oba dela sta racionalna izraza (glejte "Racionalne enačbe").

Primer:

Vsi faktorji razen enega - - tukaj so "linearni", torej vsebujejo spremenljivko samo v prvi stopnji. Take linearne faktorje potrebujemo za uporabo intervalne metode - predznak se spremeni, ko gre skozi njihove korenine. Toda množitelj sploh nima korenin. To pomeni, da je vedno pozitiven (preverite sami) in zato ne vpliva na predznak celotne neenakosti. To pomeni, da lahko nanjo razdelite levo in desno stran neenakosti in se je tako znebite:

Zdaj je vse enako, kot je bilo s kvadratnimi neenakostmi: določimo, v katerih točkah vsak od faktorjev izgine, te točke označimo na osi in razporedimo znake. Opozarjam vas na zelo pomembno dejstvo:

V primeru sodega števila ravnamo na enak način kot prej: točko obkrožimo s kvadratom in pri prehodu skozi koren ne spremenimo predznaka. Toda v primeru lihega števila to pravilo ni izpolnjeno: znak se bo ob prehodu skozi koren še vedno spremenil. Zato s takšnim korenom ne delamo ničesar dodatno, kot da ni večkratnik nas. Zgornja pravila veljajo za vse sode in lihe stopnje.

Kaj zapišemo v odgovor?

Če je zamenjava znakov kršena, morate biti zelo previdni, saj bi moral pri nestrogi neenakosti odgovor vključevati vse izpolnjene točke. Toda nekateri od njih pogosto stojijo sami, torej ne vstopajo v zasenčeno območje. V tem primeru jih dodamo odgovoru kot izolirane pike (v zavitih oklepajih):

Primeri (odločite se sami):

odgovori:

1. Če je med dejavniki preprosto - je to koren, ker ga je mogoče predstaviti kot.
   .

kjer prevzame vrednost nič. Na primer za funkcijo, podano s formulo

je nič, ker

.

Imenujejo se tudi ničle funkcije korenine funkcije.

Koncept ničel funkcije lahko upoštevamo za vse funkcije, katerih obseg vsebuje nič ali ničelni element ustrezne algebraične strukture.

Za funkcijo realne spremenljivke so ničle vrednosti, pri katerih graf funkcije seka os x.

Iskanje ničel funkcije pogosto zahteva uporabo numeričnih metod (na primer Newtonova metoda, gradientne metode).

Eden od nerešenih matematičnih problemov je iskanje ničel Riemannove zeta funkcije.

Polinomski koren

Poglej tudi

Literatura

Fundacija Wikimedia. 2010 .

Poglejte, kaj je "Function Zero" v drugih slovarjih:

Točka, kjer dana funkcija f(z) izgine; torej N. f. f (z) je enak kot korenine enačbe f (z) = 0. Na primer, točke 0, π, π, 2π, 2π,... so ničle funkcije sinz. Ničele analitične funkcije (glej Analitično ... ...

Ničelna funkcija, nič funkcija... Pravopisni slovar

Ta izraz ima druge pomene, glej nič. Vsebino tega članka je treba premakniti v članek "Funkcija nič". Projektu lahko pomagate tako, da združite članke. Če želite razpravljati o smotrnosti združitve, zamenjajte to ... Wikipedia

Ali pa je niz C (iz imena jezika C) ali niz ASCIZ (iz imena sestavljalske direktive.asciz) način predstavljanja nizov v programskih jezikih, v katerem se namesto uvedbe znaka uporablja niz znakov. posebna vrsta niza in konec ... ... Wikipedia

V kvantni teoriji polja je sprejeto (slengovsko) ime za lastnost izginotja renormalizacijskega faktorja spojne konstante, kjer je g0 gola spojna konstanta iz interakcijskega Lagrangiana, fiz. spojna konstanta, oblečena z interakcijo. Enakost Z... Fizična enciklopedija

Nulna mutacija n-alel- Ničelna mutacija, n. alel * ničelna mutacija, n. alel * ničelna mutacija ali n. alel ali tihi a. mutacija, ki vodi do popolne izgube funkcije v zaporedju DNK, v katerem se je zgodila ... Genetika. enciklopedični slovar

Izjava v teoriji verjetnosti, da ima vsak dogodek (t. i. preostali dogodek), katerega pojav določajo samo poljubno oddaljeni elementi zaporedja neodvisnih naključnih dogodkov ali naključnih spremenljivk, ... ... Matematična enciklopedija

1) Število, ki ima lastnost, da se katero koli (realno ali kompleksno) število ne spremeni, ko se mu doda. Označen je s simbolom 0. Zmnožek katerega koli števila z N. je enak N.: Če je zmnožek dveh števil enak N., potem je eden od faktorjev ... Matematična enciklopedija

Funkcije, podane z relacijami med neodvisnimi spremenljivkami, ki niso razrešene glede na slednje; ti odnosi so eden od načinov za definiranje funkcije. Na primer, relacija x2 + y2 1 = 0 definira N. f. … Velika sovjetska enciklopedija

Vrednosti argumentov z pod katerim f(z) se pokliče na nič. ničelna točka, tj. če f(a) = 0, torej a - ničelna točka.

Def. Dot ampak poklical naročilo ničn , če FKP je mogoče predstaviti v obliki f(z) = , kje
analitična funkcija in
0.

V tem primeru je pri razširitvi funkcije v Taylorjev niz (43) prvi n koeficienti so nič

= =

itd. Določite vrstni red nič za
in (1-cos z) pri z = 0

=
=

nič 1. reda

1 - cos z =
=

nič 2. reda

Def. Dot z =
poklical točka v neskončnost in nič funkcije f(z), če f(
) = 0. Taka funkcija se razširi v niz v negativnih potencih z : f(z) =
. Če najprej n koeficienti enaki nič, potem pridemo do ničelni red n v točki v neskončnosti: f(z) = z - n
.

Izolirane singularne točke delimo na: a) odstranljive singularne točke; b) naročite drogoven; v) bistvene singularne točke.

Dot ampak poklical odstranljiva singularna točka funkcije f(z) če z
a lim f(z) = od - končno število .

Dot ampak poklical pol redan (n 1) značilnosti f(z), če je inverzna funkcija
= 1/ f(z) ima vrstni red nič n na točki ampak. Takšno funkcijo lahko vedno predstavimo kot f(z) =
, kje
- analitična funkcija in
.

Dot ampak poklical bistvena točka funkcije f(z), če z
a lim f(z) ne obstaja.

Laurentova serija

Razmislite o primeru obročastega konvergenčnega območja r < | z 0 – a| < R osredotočeno na točko ampak za funkcijo f(z). Predstavljamo dva nova kroga L 1 (r) In L 2 (R) blizu meja obroča s piko z 0 med njima. Naredimo odsek obroča, združimo kroge vzdolž robov preseka, preidemo na preprosto povezano območje in v

Cauchyjeva integralna formula (39) dobimo dva integrala nad spremenljivko z

f(z 0) =
+
, (42)

kjer gre integracija v nasprotni smeri.

Za integral konec L 1 pogoj | z 0 – a | > | z – a |, in za integral čez L 2 obrnjen pogoj | z 0 – a | < | z – a |. Zato je faktor 1/( z – z 0) razširiti v niz (a) v integralu čez L 2 in v seriji (b) v integralu nad L ena . Kot rezultat dobimo razgradnjo f(z) v obročastem območju v Laurentova serija v pozitivnih in negativnih močeh ( z 0 – a)

f(z 0) =
A n (z 0 – a) n (43)

kje A n =
=
;A -n =

Širitev pozitivnih moči (z 0 - ampak) klical desni del Laurentova serija (Taylorjeva serija) in se imenuje razširitev negativnih potenk. glavni del Laurentova vrsta.

Če je znotraj kroga L 1 ni singularnih točk in je funkcija analitična, potem je v (44) prvi integral po Cauchyjevem izreku enak nič, pri razširitvi funkcije pa ostane le pravilen del. Negativne moči v ekspanziji (45) se pojavijo šele, ko je v notranjem krogu kršena analitičnost in služijo za opis funkcije v bližini izoliranih singularnih točk.

Za konstruiranje Laurentove serije (45) za f(z) lahko izračunamo ekspanzijske koeficiente po splošni formuli ali uporabimo razširitve osnovnih funkcij, vključenih v f(z).

Število izrazov ( n) glavnega dela Laurentove serije je odvisna od vrste singularne točke: odstranljiva singularna točka (n = 0) ; bistvena singularna točka (n
); palican-to naročilo(n - končna številka).

in za f(z) = pika z = 0 odstranljiva singularna točka, Ker glavnega dela ni. f(z) = (z -
) = 1 -

b) Za f(z) = pika z = 0 - Palica 1. reda

f(z) = (z -
) = -

c) Za f(z) = e 1 / z pika z = 0 - bistvena singularna točka

f(z) = e 1 / z =

Če f(z) je analitična v domeni D z izjemo m izolirane singularne točke in | z 1 | < |z 2 | < . . . < |z m| , nato pri razširitvi funkcije v pooblastilih z celotno ravnino je razdeljeno na m+ 1 prstan | z jaz | < | z | < | z jaz+ 1 | in serija Laurent ima za vsak prstan drugačno obliko. Pri širitvi pooblastil ( z – z jaz ) konvergenčno območje Laurentove vrste je krog | z – z jaz | < r, kje r je razdalja do najbližje singularne točke.

itd. Razširite funkcijo f(z) =v Laurentovi seriji v pooblastilih z in ( z - 1).

Rešitev. Funkcijo predstavljamo v obliki f(z) = - z 2 . Uporabimo formulo za vsoto geometrijske progresije
. V krogu |z|< 1 ряд сходится и f(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , tj. razgradnja vsebuje samo pravilno del. Premaknimo se na zunanje območje kroga |z| > 1 . Funkcijo predstavljamo v obliki
, kjer je 1/| z| < 1, и получим разложение f(z) = z
=z + 1 +

Ker , razširitev funkcije v pooblastilih ( z - 1) izgleda f(z) = (z - 1) -1 + 2 + (z - 1) za vse
1.

itd. Razširite funkcijo v serijo Laurent f(z) =
: a) v stopinjah z v krogu | z| < 1; b) по степеням z prstan 1< |z| < 3 ; c) по степеням (z – 2).Odločitev. Razstavimo funkcijo na preproste ulomke
= =+=
. Iz pogojev z =1
A = -1/2 , z =3
B = ½.

ampak) f(z) = ½ [
] = ½ [
-(1/3)
], ko | z|< 1.

b) f(z) = - ½ [
+
] = - (
), ob 1< |z| < 3.

od) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, za |2 - z| < 1

To je krog s polmerom 1 s središčem na točki z = 2 .

V nekaterih primerih je mogoče nize moči zmanjšati na niz geometrijskih progresij, nato pa je enostavno določiti območje njihove konvergence.

itd. Raziščite konvergenco niza

. . . + + + + 1 + () + () 2 + () 3 + . . .

Rešitev. Je vsota dveh geometrijskih progresij z q 1 = , q 2 = () . Iz pogojev njihove konvergence sledi < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Kaj so ničle funkcije? Odgovor je precej preprost - to je matematični izraz, ki pomeni domeno dane funkcije, na kateri je njena vrednost nič. Funkcijske ničle se imenujejo tudi ničle funkcij. Kaj so ničle funkcije, najlažje razložimo z nekaj preprostimi primeri.

Primeri

Razmislite o preprosti enačbi y=x+3. Ker je nič funkcije vrednost argumenta, pri katerem je y postal nič, na levi strani enačbe nadomestimo 0:

V tem primeru je -3 želena ničla. Za dano funkcijo obstaja samo en koren enačbe, vendar to ni vedno tako.

Razmislite o drugem primeru:

Zamenjajte 0 na levi strani enačbe, kot v prejšnjem primeru:

Očitno bosta v tem primeru dve ničli funkcije: x=3 in x=-3. Če bi enačba imela argument tretje stopnje, bi bile tri ničle. Lahko naredimo preprost sklep, da število korenov polinoma ustreza največji stopnji argumenta v enačbi. Vendar pa je veliko funkcij, na primer y=x 3 , na prvi pogled v nasprotju s to trditvijo. Logika in zdrav razum nakazujeta, da ima ta funkcija samo eno ničlo - v točki x=0. Toda v resnici obstajajo tri korenine, le vse sovpadajo. Če enačbo rešite v kompleksni obliki, postane to očitno. x=0 v tem primeru je koren, katerega večkratnost je 3. V prejšnjem primeru se ničle niso ujemale, zato so imele večkratnost 1.

Definicijski algoritem

Iz predstavljenih primerov je jasno, kako določiti ničle funkcije. Algoritem je vedno enak:

1. Napišite funkcijo.
2. Zamenjaj y ali f(x)=0.
3. Rešite dobljeno enačbo.

Kompleksnost zadnje postavke je odvisna od stopnje argumenta enačbe. Pri reševanju enačb visokih stopenj je še posebej pomembno zapomniti, da je število korenov enačbe enako največji moči argumenta. To še posebej velja za trigonometrične enačbe, kjer deljenje obeh delov s sinusom ali kosinusom vodi do izgube korenin.

Enačbe poljubnih stopenj najlažje rešujemo s Hornerjevo metodo, ki je bila razvita posebej za iskanje ničel poljubnega polinoma.

Vrednost ničel funkcij je lahko negativna in pozitivna, realna ali ležeča v kompleksni ravnini, enojna ali večkratna. Ali pa morda ni korenin enačbe. Na primer, funkcija y=8 ne bo postala nič za noben x, ker ni odvisna od te spremenljivke.

Enačba y=x 2 -16 ima dva korena in obe ležita v kompleksni ravnini: x 1 =4i, x 2 =-4i.

Pogoste napake

Pogosta napaka šolarjev, ki še niso zares ugotovili, kaj so ničle funkcije, je zamenjava argumenta (x) z ničlo in ne vrednosti (y) funkcije. V enačbo samozavestno nadomestijo x = 0 in na podlagi tega poiščejo y. Toda to je napačen pristop.

Druga napaka, kot že omenjeno, je redukcija s sinusom ali kosinusom v trigonometrični enačbi, zaradi česar se ena ali več ničel funkcije izgubi. To ne pomeni, da v takšnih enačbah ni mogoče ničesar zmanjšati, vendar je treba te »izgubljene« faktorje upoštevati pri nadaljnjih izračunih.

Grafična predstavitev

Kaj so ničle funkcije, lahko razumete s pomočjo matematičnih programov, kot je Maple. V njem lahko zgradite graf tako, da določite želeno število točk in želeno lestvico. Tiste točke, na katerih graf prečka os OX, so želene ničle. To je eden najhitrejših načinov za iskanje korenin polinoma, še posebej, če je njegov vrstni red višji od tretjega. Če je torej treba redno izvajati matematične izračune, poiskati korenine polinomov poljubnih stopenj, zgraditi grafe, bo Maple ali podoben program preprosto nepogrešljiv za izvajanje in preverjanje izračunov.

Matematični prikaz funkcije jasno kaže, kako ena količina v celoti določa vrednost druge količine. Tradicionalno veljajo številčne funkcije, ki povezujejo eno število z drugim. Nič funkcije se običajno imenuje vrednost argumenta, pri katerem funkcija izgine.

Navodilo

1. Če želite najti ničle funkcije, morate njeno desno stran enačiti z ničlo in rešiti nastalo enačbo. Predstavljajte si, da vam je dana funkcija f(x)=x-5.

2. Da bi našli ničle te funkcije, vzemimo in enačimo njeno desno stran z ničlo: x-5=0.

3. Če rešimo to enačbo, dobimo, da je x=5 in ta vrednost argumenta bo nič funkcije. To pomeni, da ko je vrednost argumenta 5, funkcija f(x) izgine.

V oddaji funkcije pri matematiki razumeti razmerje med elementi množic. Če povedano bolj pravilno, gre za "zakon", po katerem je celotnemu elementu ene množice (imenovano domena definicije) dodeljen določen element drugega niza (imenovano domena vrednosti).

Boste potrebovali

• Znanje iz algebre in matematični pregled.

Navodilo

1. Vrednote funkcije to je določeno področje, iz katerega lahko funkcija prevzame vrednosti. Recimo razpon funkcije f(x)=|x| od 0 do neskončnosti. Odkriti pomen funkcije na določeni točki morate argument nadomestiti funkcije njegov številčni ekvivalent bo dobljeno število pomen m funkcije. Naj bo funkcija f(x)=|x| – 10 + 4x. odkriti pomen funkcije v točki x=-2. Namesto x zamenjajte številko -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. tj pomen funkcije v točki -2 je -16.

Opomba!
Preden iščete vrednost funkcije na točki, se prepričajte, da je vključena v obseg funkcije.

Koristni nasveti
S podobno metodo je mogoče najti vrednost funkcije več argumentov. Razlika je v tem, da boste morali namesto ene številke zamenjati več - glede na število argumentov funkcije.

Funkcija je vzpostavljena relacija spremenljivke y od spremenljivke x. Poleg tega celotna vrednost x, imenovana argument, ustreza izjemni vrednosti y - funkciji. V grafični obliki je funkcija prikazana v kartezičnem koordinatnem sistemu v obliki grafa. Točke presečišča grafa z abscisno osjo, na katerih so izrisani argumenti x, se imenujejo ničle funkcije. Iskanje veljavnih ničel je ena od nalog iskanja dane funkcije. V tem primeru se upoštevajo vse dopustne vrednosti neodvisne spremenljivke x, ki tvorijo domeno definicije funkcije (OOF).

Navodilo

1. Nič funkcije je vrednost argumenta x, pri kateri je vrednost funkcije nič. Vendar so lahko ničle le tisti argumenti, ki so vključeni v področje definicije preučevane funkcije. Se pravi, pri tako veliko vrednostih, za katere ima funkcija f (x) smisel.

2. Zapišite dano funkcijo in jo enačite z nič, recimo f(x) = 2x?+5x+2 = 0. Rešite dobljeno enačbo in poiščite njene realne korenine. Korenine kvadratne enačbe se izračunajo s podporo iskanja diskriminante. 2x? + 5x + 2 \u003d 0; D = b? -4ac = 5? -4 * 2 * 2 = 9; x1 = (-b +? D) / 2 * a = (-5 + 3) / 2 * 2 \u003d -0,5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2. Tako sta v tem primeru dva dobimo korenine kvadratne enačbe, ki ustrezajo argumentom začetne funkcije f(x).

3. Preverite, ali vse zaznane vrednosti x pripadajo domeni definicije dane funkcije. Zaznaj OOF, za to preveri začetni izraz za prisotnost korenov sode stopnje oblike? f (x), za prisotnost ulomkov v funkciji z argumentom v imenovalcu, za prisotnost logaritmičnih oz. trigonometrični izrazi.

4. Ko upoštevate funkcijo z izrazom pod korenom sode stopnje, vzemite za domeno definicije vse argumente x, katerih vrednosti ne spremenijo korenskega izraza v negativno število (nasprotno, funkcija naredi nima smisla). Določite, ali zaznane ničle funkcije spadajo v določen obseg sprejemljivih vrednosti x.

5. Imenovalec ulomka ne more izginiti, zato izključite tiste argumente x, ki vodijo do takega rezultata. Za logaritemske količine je treba upoštevati le tiste vrednosti argumenta, za katere je sam izraz večji od nič. Funkcijske ničle, ki spremenijo sublogaritemski izraz v nič ali negativno število, je treba zavreči iz končnega rezultata.

Opomba!
Pri iskanju korenin enačbe se lahko pojavijo dodatni koreni. To je enostavno preveriti: dovolj je, da dobljeno vrednost argumenta nadomestimo v funkcijo in se prepričamo, da funkcija izgine.

Koristni nasveti
Občasno funkcija ni eksplicitno izražena s svojim argumentom, potem je enostavno vedeti, kaj je funkcija. Primer tega je enačba kroga.