Nule funkcije prema rasporedu. Funkcija nula. Pravilo nulte funkcije

Funkcija jedan je od najvažnijih matematičkih pojmova. Funkcija - varijabla ovisnost na iz varijable x, ako je svaka vrijednost x odgovara jednoj vrijednosti na. varijabla x naziva neovisna varijabla ili argument. varijabla na naziva zavisna varijabla. Sve vrijednosti nezavisne varijable (varijable x) čine domenu funkcije. Sve vrijednosti koje zavisna varijabla uzima (varijabla y), čine raspon funkcije.

Grafikon funkcije nazivaju skup svih točaka koordinatne ravnine, čije su apscise jednake vrijednostima argumenta, a ordinate jednake odgovarajućim vrijednostima funkcije, odnosno vrijednostima varijable su iscrtane duž apscisne osi x, a vrijednosti varijable su iscrtane duž y osi y. Da biste nacrtali funkciju, morate znati svojstva funkcije. Glavna svojstva funkcije bit će razmotrena u nastavku!

Za crtanje grafa funkcije preporučujemo korištenje našeg programa - Graphing Functions Online. Ako imate bilo kakvih pitanja tijekom proučavanja materijala na ovoj stranici, uvijek ih možete postaviti na našem forumu. Također na forumu će vam se pomoći u rješavanju zadataka iz matematike, kemije, geometrije, teorije vjerojatnosti i mnogih drugih predmeta!

Osnovna svojstva funkcija.

1) Opseg funkcije i raspon funkcija.

Opseg funkcije je skup svih valjanih vrijednosti argumenta x(promjenjivo x) za koje je funkcija y = f(x) definiran.
Raspon funkcije je skup svih realnih vrijednosti y da funkcija prihvaća.

U osnovnoj matematici funkcije se proučavaju samo na skupu realnih brojeva.

2) Nule funkcije.

Nula funkcije je vrijednost argumenta kod koje je vrijednost funkcije jednaka nuli.

3) Intervali konstantnosti predznaka funkcije.

Intervali konstantnog predznaka funkcije su takvi skupovi vrijednosti argumenata na kojima su vrijednosti funkcije samo pozitivne ili samo negativne.

4) Monotonost funkcije.

Povećana funkcija (u određenom intervalu) je funkcija u kojoj veća vrijednost argumenta iz ovog intervala odgovara većoj vrijednosti funkcije.

Opadajuća funkcija (u nekom intervalu) - funkcija u kojoj veća vrijednost argumenta iz ovog intervala odgovara manjoj vrijednosti funkcije.

5) Parne (neparne) funkcije.

Parna funkcija je funkcija čija je domena definicije simetrična u odnosu na ishodište i za bilo koje x iz domene definicije jednakost f(-x) = f(x). Graf parne funkcije je simetričan u odnosu na y-os.

Neparna funkcija je funkcija čija je domena definicije simetrična u odnosu na ishodište i za bilo koje x iz domene definicije jednakost f(-x) = - f(x). Graf neparne funkcije je simetričan u odnosu na ishodište.

6) Ograničene i neograničene funkcije.

Funkcija se naziva ograničenom ako postoji pozitivan broj M takav da je |f(x)| ≤ M za sve vrijednosti x. Ako takvog broja nema, funkcija je neograničena.

7) Periodičnost funkcije.

Funkcija f(x) je periodična ako postoji broj T koji nije nula takav da je za bilo koji x f(x+T) = f(x). Ovaj najmanji broj naziva se period funkcije. Sve trigonometrijske funkcije su periodične. (Trigonometrijske formule).

Nakon što ste proučili ova svojstva funkcije, možete jednostavno istražiti funkciju i, koristeći svojstva funkcije, možete nacrtati graf funkcije. Također pogledajte materijal o tablici istinitosti, tablici množenja, periodnom sustavu, tablici derivacija i tablici integrala.

Nule funkcije

Što su funkcije nule? Kako analitički i grafički odrediti nule funkcije?

Nule funkcije su vrijednosti argumenta kod kojih je funkcija jednaka nuli.

Da bismo pronašli nule funkcije zadane formulom y=f(x), trebamo riješiti jednadžbu f(x)=0.

Ako jednadžba nema korijena, tada funkcija nema nule.

1) Pronađite nule linearne funkcije y=3x+15.

Da bismo pronašli nule funkcije, rješavamo jednadžbu 3x+15 =0.

Dakle, nula funkcije je y=3x+15 - x= -5 .

2) Pronađite nule kvadratne funkcije f(x)=x²-7x+12.

Da bismo pronašli nule funkcije, rješavamo kvadratnu jednadžbu

Njegovi korijeni x1=3 i x2=4 su nule ove funkcije.

3) Pronađite nule funkcije

Razlomak ima smisla ako je nazivnik različit od nule. Dakle, x²-1≠0, x² ≠ 1,x ≠±1. Odnosno, domena definicije ove funkcije (ODZ)

Iz korijena jednadžbe x²+5x+4=0 x1=-1 x2=-4, samo je x=-4 uključeno u domenu definicije.

Da bismo pronašli nule funkcije zadane grafički, potrebno je pronaći točke presjeka grafa funkcije s osi x.

Ako graf ne prelazi os Ox, funkcija nema nule.

funkcija čiji je graf prikazan na slici ima četiri nule -

U algebri se problem pronalaženja nula funkcije javlja i kao samostalan zadatak i pri rješavanju drugih problema, na primjer, pri proučavanju funkcije, rješavanju nejednakosti itd.

www.algebraclass.ru

Pravilo nulte funkcije

Osnovni pojmovi i svojstva funkcija

Pravilo (zakon) sukladnosti. Monotonska funkcija .

Ograničene i neograničene funkcije. Kontinuirano i

diskontinuirana funkcija . Parne i neparne funkcije.

Periodična funkcija. Razdoblje funkcije.

Nule funkcije . Asimptota .

Opseg i raspon funkcije. U osnovnoj matematici funkcije se proučavaju samo na skupu realnih brojeva R . To znači da argument funkcije može poprimiti samo one stvarne vrijednosti za koje je funkcija definirana, tj. također prihvaća samo stvarne vrijednosti. Mnogo x sve važeće važeće vrijednosti argumenta x, za koji je funkcija y = f (x) definira se, zove se opseg funkcije. Mnogo Y sve stvarne vrijednosti y koju funkcija prihvaća poziva se raspon funkcija. Sada možemo dati precizniju definiciju funkcije: Pravilo (zakon) korespondencije između skupova x I Y , kojim se za svaki element iz skupa x možete pronaći jedan i samo jedan element iz skupa Y, naziva se funkcija .

Iz ove definicije slijedi da se funkcija smatra danom ako:

- opseg funkcije je postavljen x ;

— postavljen je raspon vrijednosti funkcije Y ;

- poznato je pravilo (zakon) korespondencije, i to takvo da za svaku

vrijednosti argumenata, može se pronaći samo jedna vrijednost funkcije.

Ovaj zahtjev jedinstvenosti funkcije je obavezan.

monotonska funkcija. Ako za bilo koje dvije vrijednosti argumenta x 1 i x 2 uvjeta x 2 > x 1 slijedi f (x 2) > f (x 1), zatim funkciju f (x) Zove se povećavajući; ako za bilo koji x 1 i x 2 uvjeta x 2 > x 1 slijedi f (x 2)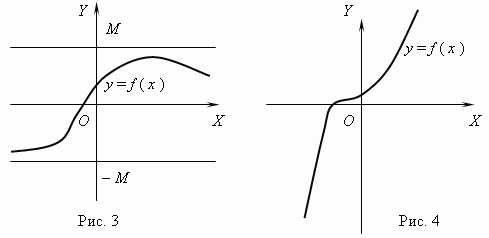

Funkcija prikazana na slici 3 je ograničena, ali nije monotona. Funkcija na slici 4 je upravo suprotna, monotona, ali neograničena. (Objasnite ovo molim vas!)

Kontinuirane i diskontinuirane funkcije. Funkcija y = f (x) Zove se stalan u točki x = a, ako:

1) funkcija je definirana za x = a, tj. e. f (a) postoji;

2) postoji konačan granica lim f (x) ;

Ako barem jedan od ovih uvjeta nije ispunjen, funkcija se poziva diskontinuiran u točki x = a .

Ako je funkcija kontinuirana u svi točke njegove domene definicije, onda se zove kontinuirana funkcija.

Parne i neparne funkcije. Ako za bilo koji x iz opsega definicije funkcije odvija se: f (— x) = f (x), tada se poziva funkcija čak; ako radi: f (— x) = — f (x), tada se poziva funkcija neparan. Grafikon parne funkcije simetrično oko Y osi(Sl.5), graf neparne funkcije Sim metrika o podrijetlu(slika 6).

Periodična funkcija. Funkcija f (x) — časopis ako postoji takav različit od nule broj T za što bilo koji x iz opsega definicije funkcije odvija se: f (x + T) = f (x). Takav najmanje broj se zove razdoblje funkcije. Sve trigonometrijske funkcije su periodične.

PRIMJER 1. Dokaži taj grijeh x ima period od 2.

RJEŠENJE Znamo da je grijeh ( x + 2 n) = grijeh x, gdje n= 0, ± 1, ± 2, …

Stoga, dodajući 2 n na argument sinusa

mijenja svoju vrijednost e . Postoji li drugi broj s ovim

Pretvarajmo se to P- takav broj, tj. jednakost:

vrijedi za bilo koju vrijednost x. Ali onda ima

mjestu i na x= / 2, tj. e.

grijeh(/2 + P) = sin / 2 = 1.

Ali prema formuli redukcije sin (/ 2 + P) = cos P. Zatim

iz posljednje dvije jednakosti proizlazi da cos P= 1, ali mi

Znamo da to vrijedi samo za P = 2 n. Od najmanjih

broj različit od nule od 2 n je 2, onda je ovaj broj

i postoji period grijeh x. Slično se dokazuje da 2

je razdoblje za cos x .

Dokazati da su funkcije tan x i mačka x imati mjesečnicu.

Primjer 2. Koji je broj period funkcije sin 2 x ?

Rješenje. Razmotrimo grijeh 2 x= sin (2 x + 2 n) = sin [ 2 ( x + n) ] .

Vidimo to dodavanje n na argument x, ne mijenja se

vrijednost funkcije. Najmanji broj različit od nule

iz n je , pa je ovo period sin 2 x .

Null funkcije. Poziva se vrijednost argumenta za koji je funkcija jednaka 0 nula ( root) funkcije. Funkcija može imati više nula. Na primjer, funkcija y = x (x + 1) (x- 3) ima tri nule: x = 0, x = — 1, x= 3. Geometrijski funkcija null – je apscisa točke presjeka grafa funkcije s osi x .

Slika 7 prikazuje graf funkcije s nulama: x = a , x = b I x = c .

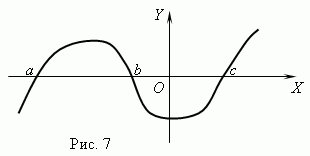
Asimptota. Ako se graf funkcije neograničeno približava određenoj ravnoj liniji dok se udaljava od ishodišta, tada se ta ravna linija naziva asimptota.

Tema 6. "Metoda intervala".

Ako je f (x) f (x 0) za x x 0, tada se poziva funkcija f (x). kontinuirano na x 0.

Ako je funkcija kontinuirana u svakoj točki nekog intervala I, onda se zove kontinuirano na intervalu I (interval I se zove interval kontinuiteta funkcije). Graf funkcije na ovom intervalu je neprekidna crta, za koju se kaže da je "nacrtana bez podizanja olovke s papira".

Svojstvo kontinuiranih funkcija.

Ako je na intervalu (a ; b) funkcija f neprekidna i ne nestaje, ona zadržava stalan predznak na tom intervalu.

Metoda rješavanja nejednadžbi s jednom varijablom temelji se na ovom svojstvu – metodi intervala. Neka je funkcija f(x) kontinuirana na intervalu I i nestaje u konačnom broju točaka u tom intervalu. Svojstvom neprekidnih funkcija te točke dijele I na intervale, u svakom od kojih kontinuirana funkcija f(x) c čuva stalni predznak. Za određivanje ovog predznaka dovoljno je izračunati vrijednost funkcije f(x) u bilo kojoj točki iz svakog takvog intervala. Na temelju toga dobivamo sljedeći algoritam za rješavanje nejednadžbi metodom intervala.

Intervalna metoda za nejednakosti oblika

Pronađite domenu funkcije f(x) ;

Pronađite nule funkcije f(x) ;

Na brojevnoj liniji nacrtajte domenu definicije i nule funkcije. Nule funkcije dijele njezino područje definicije na intervale, u svakom od kojih funkcija zadržava konstantan predznak;

Pronađite predznake funkcije u dobivenim intervalima izračunavanjem vrijednosti funkcije u bilo kojoj točki iz svakog intervala;

Zapišite odgovor.

intervalna metoda. Prosječna razina.

Želite li isprobati svoju snagu i saznati rezultat koliko ste spremni za Jedinstveni državni ispit ili OGE?

Linearna funkcija

Funkcija oblika naziva se linearna. Uzmimo funkciju kao primjer. Pozitivan je na 3″> i negativan na. Točka je nula funkcije (). Pokažimo predznake ove funkcije na realnoj osi:

Kažemo da "funkcija mijenja predznak kada prolazi kroz točku".

Vidi se da predznaci funkcije odgovaraju položaju grafa funkcije: ako je graf iznad osi, znak je “ ”, ako je ispod nje “ ”.

Ako generaliziramo rezultirajuće pravilo na proizvoljnu linearnu funkciju, dobivamo sljedeći algoritam:

Nalazimo nulu funkcije;

Obilježavamo ga na brojčanoj osi;

Određujemo predznak funkcije na suprotnim stranama nule.

kvadratna funkcija

Nadam se da se sjećate kako se rješavaju kvadratne nejednadžbe? Ako ne, pročitajte temu "Kvadratne nejednakosti". Dopustite mi da vas podsjetim na opći oblik kvadratne funkcije: .

Prisjetimo se sada koje znakove ima kvadratna funkcija. Njegov graf je parabola, a funkcija uzima znak “ ” za one u kojima je parabola iznad osi, a “ ” - ako je parabola ispod osi:

Ako funkcija ima nule (vrijednosti na kojima), parabola siječe os u dvije točke - korijene odgovarajuće kvadratne jednadžbe. Tako je os podijeljena na tri intervala, a predznaci funkcije se naizmjenično mijenjaju pri prolasku kroz svaki korijen.

Je li moguće nekako odrediti znakove bez crtanja parabole svaki put?

Podsjetimo da se kvadratni trinom može faktorizirati:

Obratite pažnju na korijene na osi:

Sjećamo se da se predznak funkcije može promijeniti samo pri prolasku kroz korijen. Koristimo se ovom činjenicom: za svaki od tri intervala na koje je os podijeljena korijenima, dovoljno je odrediti predznak funkcije samo u jednoj proizvoljno odabranoj točki: u ostalim točkama intervala predznak će biti isti.

U našem primjeru: za 3″> oba izraza u zagradama su pozitivna (zamjenjujemo, na primjer: 0″>). Stavili smo znak "" na os:

Pa, ako su (zamjena, na primjer) obje zagrade negativne, onda je proizvod pozitivan:

To je ono što je intervalna metoda: poznavajući predznake faktora na svakom intervalu, određujemo predznak cijelog proizvoda.

Razmotrimo i slučajeve kada funkcija nema nule ili je samo jedna.

Ako ih nema, onda nema ni korijena. To znači da neće biti "prolaska kroz korijen". To znači da funkcija na cijeloj brojevnoj osi ima samo jedan predznak. Lako je odrediti zamjenom u funkciju.

Ako postoji samo jedan korijen, parabola dodiruje os, pa se predznak funkcije ne mijenja pri prolasku kroz korijen. Koje je pravilo za takve situacije?

Ako odvojimo takvu funkciju, dobivamo dva identična faktora:

I svaki izraz na kvadrat nije negativan! Stoga se predznak funkcije ne mijenja. U takvim slučajevima ćemo odabrati korijen, pri prolasku kroz koji se znak ne mijenja, zaokružujući ga kvadratom:

Takav korijen će se zvati višestruko.

Metoda intervala u nejednačinama

Sada se svaka kvadratna nejednakost može riješiti bez crtanja parabole. Dovoljno je samo postaviti predznake kvadratne funkcije na os, a intervale odabrati ovisno o predznaku nejednakosti. Na primjer:

Mjerimo korijenje na osi i raspoređujemo znakove:

Trebamo dio osi sa znakom ""; budući da nejednakost nije stroga, u rješenje su uključeni i sami korijeni:

Sada razmotrite racionalnu nejednakost - nejednakost, čija su oba dijela racionalni izrazi (vidi "Racionalne jednadžbe").

Primjer:

Svi faktori osim jednog - - ovdje su "linearni", odnosno sadrže varijablu samo u prvom stupnju. Takvi linearni faktori su nam potrebni za primjenu intervalne metode – predznak se mijenja pri prolasku kroz njihove korijene. Ali množitelj uopće nema korijen. To znači da je uvijek pozitivan (provjerite sami), te stoga ne utječe na predznak cijele nejednakosti. To znači da možete podijeliti lijevu i desnu stranu nejednakosti na nju i tako je se riješiti:

Sada je sve isto kao što je bilo s kvadratnim nejednakostima: odredimo u kojim točkama svaki od faktora nestaje, označimo te točke na osi i rasporedimo znakove. Skrećem vam pažnju na jednu vrlo važnu činjenicu:

U slučaju parnog broja postupamo na isti način kao i prije: točku zaokružujemo kvadratom i ne mijenjamo predznak pri prolasku kroz korijen. Ali u slučaju neparnog broja, ovo pravilo nije ispunjeno: znak će se i dalje mijenjati kada prolazi kroz korijen. Stoga s takvim korijenom ne radimo ništa dodatno, kao da nije višestruki od nas. Gornja pravila vrijede za sve parne i neparne potencije.

Što pišemo u odgovoru?

Ako je izmjena znakova prekršena, morate biti vrlo oprezni, jer uz nestrogu nejednakost, odgovor bi trebao uključivati sve popunjene točke. Ali neki od njih često stoje sami, odnosno ne ulaze u zasjenjeno područje. U ovom slučaju, dodamo ih odgovoru kao izolirane točke (u vitičastim zagradama):

Primjeri (odlučite sami):

odgovori:

1. Ako je među čimbenicima jednostavno - to je korijen, jer se može predstaviti kao.
   .

gdje poprima vrijednost nula. Na primjer, za funkciju zadanu formulom

je ništavan jer

.

Zove se i nule funkcije korijeni funkcije.

Koncept nula funkcije može se uzeti u obzir za sve funkcije čiji raspon sadrži nulu ili nulti element odgovarajuće algebarske strukture.

Za funkciju stvarne varijable, nule su vrijednosti na kojima graf funkcije siječe x-os.

Pronalaženje nula funkcije često zahtijeva korištenje numeričkih metoda (na primjer, Newtonova metoda, metode gradijenta).

Jedan od neriješenih matematičkih problema je pronalaženje nula Riemannove zeta funkcije.

Korijen polinoma

vidi također

Književnost

Zaklada Wikimedia. 2010 .

Pogledajte što je "Function Zero" u drugim rječnicima:

Točka u kojoj zadana funkcija f(z) nestaje; dakle, N. f. f (z) je isto što i korijeni jednadžbe f (z) = 0. Na primjer, točke 0, π, π, 2π, 2π,... su nule sinz funkcije. Nule analitičke funkcije (vidi Analitičko ... ...

Nula funkcija, nula funkcija... Pravopisni rječnik

Ovaj izraz ima druga značenja, vidi Nulu. Sadržaj ovog članka potrebno je premjestiti u članak "Funkcija nula". Možete pomoći projektu objedinjavanjem članaka. Ako trebate razgovarati o preporučljivosti spajanja, zamijenite ovo ... Wikipedia

Ili C string (iz naziva C jezika) ili ASCIZ niz (iz naziva asemblerske direktive.asciz) je način predstavljanja nizova u programskim jezicima, u kojem se koristi niz znakova umjesto uvođenja posebna vrsta stringa, a kraj ... ... Wikipedia

U kvantnoj teoriji polja, prihvaćen (sleng) naziv za svojstvo nestajanja faktora renormalizacije konstante spajanja, gdje je g0 gola konstanta spajanja iz interakcijskog Lagrangiana, fiz. spojna konstanta odjevena interakcijom. Jednakost Z... Fizička enciklopedija

Null mutacija n-alel- Null mutacija, n. alel * nulta mutacija, n. alel * nulta mutacija ili n. alel ili tihi a. mutacija koja dovodi do potpunog gubitka funkcije u sekvenci DNK u kojoj se dogodila... Genetika. enciklopedijski rječnik

Tvrdnja u teoriji vjerojatnosti da svaki događaj (tzv. rezidualni događaj), čija je pojava određena samo proizvoljno udaljenim elementima niza neovisnih slučajnih događaja ili slučajnih varijabli, ima ... ... Matematička enciklopedija

1) Broj koji ima svojstvo da se bilo koji (stvarni ili kompleksni) broj ne mijenja kada mu se doda. Označava se simbolom 0. Umnožak bilo kojeg broja s N. jednak je N.: Ako je umnožak dvaju brojeva jednak N., tada je jedan od faktora ... Matematička enciklopedija

Funkcije zadane relacijama između nezavisnih varijabli koje nisu razriješene s obzirom na potonje; ti su odnosi jedan od načina definiranja funkcije. Na primjer, relacija x2 + y2 1 = 0 definira N. f. … Velika sovjetska enciklopedija

Vrijednosti argumenata z pod kojim f(z) ide na nulu zove. nulta točka, tj. ako f(a) = 0, dakle a - nulta točka.

Def. Točka ali pozvao red nulan , ako FKP se može predstaviti u obliku f(z) = , gdje
analitička funkcija i
0.

U ovom slučaju, u proširenju funkcije u Taylorov niz (43), prvi n koeficijenti su nula

= =

itd. Odrediti red nule za
i (1-cos z) na z = 0

=
=

nula 1. reda

1 - cos z =
=

nula 2. reda

Def. Točka z =
pozvao točka u beskonačnost I nula funkcije f(z), ako f(
) = 0. Takva se funkcija širi u niz negativnih potencija z : f(z) =
. Ako prvi n koeficijenti su jednaki nuli, tada dolazimo do nulti red n u točki u beskonačnosti: f(z) = z - n
.

Izolirane singularne točke dijele se na: a) uklonjive singularne točke; b) naručiti stupoven; u) bitne singularne točke.

Točka ali pozvao uklonjiva singularna točka funkcije f(z) ako z
a lim f(z) = od - konačan broj .

Točka ali pozvao stup redan (n 1) značajke f(z) ako je inverzna funkcija
= 1/ f(z) ima nulti red n u točki ali. Takva se funkcija uvijek može predstaviti kao f(z) =
, gdje
- analitička funkcija i
.

Točka ali pozvao bitna točka funkcije f(z), ako z
a lim f(z) ne postoji.

Laurent serija

Razmotrimo slučaj prstenastog područja konvergencije r < | z 0 – a| < R centriran na točku ali za funkciju f(z). Predstavljamo dva nova kruga L 1 (r) I L 2 (R) blizu granica prstena s točkom z 0 između njih. Napravimo dio prstena, spojimo krugove duž rubova presjeka, prijeđimo na jednostavno povezano područje i u

Formulom Cauchyjevog integrala (39) dobivamo dva integrala nad varijablom z

f(z 0) =
+
, (42)

gdje integracija ide u suprotnim smjerovima.

Za integral preko L 1 uvjet | z 0 – a | > | z – a |, a za integral preko L 2 obrnuti uvjet | z 0 – a | < | z – a |. Stoga je faktor 1/( z – z 0) proširiti u niz (a) u integralu preko L 2 i u nizu (b) u integralu preko L jedan . Kao rezultat, dobivamo razgradnju f(z) u prstenastom području u Laurent serija u pozitivnim i negativnim snagama ( z 0 – a)

f(z 0) =
A n (z 0 – a) n (43)

gdje A n =
=
;A -n =

Ekspanzija u pozitivnim moćima (z 0 - ali) pozvao desni dio Laurentov niz (Taylorov niz), a ekspanzija u negativnim potencijama naziva se. glavni dio Laurent red.

Ako je unutar kruga L 1 nema singularnih točaka i funkcija je analitička, tada je u (44) prvi integral jednak nuli po Cauchyevom teoremu, a u proširenju funkcije ostaje samo ispravan dio. Negativne snage u ekspanziji (45) pojavljuju se samo kada je narušena analitičnost unutar unutarnjeg kruga i služe za opisivanje funkcije u blizini izoliranih singularnih točaka.

Za konstruiranje Laurentovog niza (45) za f(z) može se izračunati koeficijente ekspanzije prema općoj formuli ili koristiti proširenja elementarnih funkcija uključenih u f(z).

Broj pojmova ( n) glavnog dijela Laurentovog niza ovisi o vrsti singularne točke: uklonjiva singularna točka (n = 0) ; bitna singularna točka (n
); poln-ti red(n - krajnji broj).

i za f(z) = točka z = 0 singularna točka koja se može ukloniti, jer nema glavnog dijela. f(z) = (z -
) = 1 -

b) Za f(z) = točka z = 0 - stup 1. reda

f(z) = (z -
) = -

c) Za f(z) = e 1 / z točka z = 0 - bitna singularna točka

f(z) = e 1 / z =

Ako f(z) je analitičan u domeni D uz iznimku m izolirane singularne točke i | z 1 | < |z 2 | < . . . < |z m| , zatim kod proširenja funkcije u ovlasti z cijela je ravnina podijeljena na m+ 1 prsten | z i | < | z | < | z i+ 1 | a serija Laurent ima drugačiji oblik za svaki prsten. Prilikom proširenja ovlasti ( z – z i ) područje konvergencije Laurentovog reda je kružnica | z – z i | < r, gdje r je udaljenost do najbliže singularne točke.

itd. Proširite funkciju f(z) =u Laurenovoj seriji u moćima z i ( z - 1).

Riješenje. Funkciju predstavljamo u obliku f(z) = - z 2 . Koristimo formulu za zbroj geometrijske progresije
. U krugu |z|< 1 ряд сходится и f(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , tj. razlaganje sadrži samo ispravan dio. Prijeđimo na vanjsko područje kružnice |z| > 1 . Funkciju predstavljamo u obliku
, gdje je 1/| z| < 1, и получим разложение f(z) = z
=z + 1 +

Jer , proširenje funkcije u ovlasti ( z - 1) izgleda f(z) = (z - 1) -1 + 2 + (z - 1) za svakoga
1.

itd. Proširite funkciju u Laurentovom nizu f(z) =
: a) u stupnjevima z u krugu | z| < 1; b) по степеням z prsten 1< |z| < 3 ; c) по степеням (z – 2).Odluka. Razložimo funkciju na jednostavne razlomke
= =+=
. Iz uvjeta z =1
A = -1/2 , z =3
B = ½.

ali) f(z) = ½ [
] = ½ [
-(1/3)
], kada | z|< 1.

b) f(z) = - ½ [
+
] = - (
), u 1< |z| < 3.

iz) f(z) = ½ [
]= - ½ [
] =

= - ½ = -
, za |2 - z| < 1

To je kružnica polumjera 1 sa središtem u točki z = 2 .

U nekim slučajevima, nizovi se mogu svesti na skup geometrijskih progresija, a zatim je lako odrediti područje njihove konvergencije.

itd. Istražiti konvergenciju niza

. . . + + + + 1 + () + () 2 + () 3 + . . .

Riješenje. To je zbroj dviju geometrijskih progresija s q 1 = , q 2 = () . Iz uvjeta njihove konvergencije slijedi < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Što su funkcije nule? Odgovor je prilično jednostavan - ovo je matematički pojam, koji označava domenu dane funkcije, na kojoj je njezina vrijednost nula. Nule funkcije nazivaju se i nule funkcije Najlakši način da objasnite što su nule funkcije je s nekoliko jednostavnih primjera.

Primjeri

Razmotrimo jednostavnu jednadžbu y=x+3. Budući da je nula funkcije vrijednost argumenta pri kojem je y postao nula, zamjenjujemo 0 na lijevoj strani jednadžbe:

U ovom slučaju, -3 je željena nula. Za danu funkciju postoji samo jedan korijen jednadžbe, ali to nije uvijek slučaj.

Razmotrimo još jedan primjer:

Zamijenite 0 na lijevoj strani jednadžbe, kao u prethodnom primjeru:

Očito, u ovom slučaju, bit će dvije nule funkcije: x=3 i x=-3. Kad bi jednadžba imala argument trećeg stupnja, postojale bi tri nule. Možemo donijeti jednostavan zaključak da broj korijena polinoma odgovara maksimalnom stupnju argumenta u jednadžbi. Međutim, mnoge funkcije, na primjer y=x 3 , na prvi pogled su u suprotnosti s ovom tvrdnjom. Logika i zdrav razum sugeriraju da ova funkcija ima samo jednu nulu - u točki x=0. Ali zapravo postoje tri korijena, samo se svi poklapaju. Ako jednadžbu riješite u složenom obliku, to postaje očito. x=0 u ovom slučaju, korijen čiji je višestrukost 3. U prethodnom primjeru nule se nisu podudarale, pa su imale višestrukost 1.

Algoritam definicije

Iz prikazanih primjera jasno je kako odrediti nule funkcije. Algoritam je uvijek isti:

1. Napišite funkciju.
2. Zamijenite y ili f(x)=0.
3. Riješi dobivenu jednadžbu.

Složenost posljednje stavke ovisi o stupnju argumenta jednadžbe. Prilikom rješavanja jednadžbi visokih stupnjeva, posebno je važno zapamtiti da je broj korijena jednadžbe jednak maksimalnoj snazi ​​argumenta. To posebno vrijedi za trigonometrijske jednadžbe, gdje dijeljenje oba dijela sinusom ili kosinusom dovodi do gubitka korijena.

Jednadžbe proizvoljnih stupnjeva najlakše se rješavaju Hornerovom metodom koja je razvijena posebno za pronalaženje nula proizvoljnog polinoma.

Vrijednost nula funkcija može biti i negativna i pozitivna, stvarna ili ležati u kompleksnoj ravnini, pojedinačna ili višestruka. Ili možda nema korijena jednadžbe. Na primjer, funkcija y=8 neće postati nula za bilo koji x, jer ne ovisi o ovoj varijabli.

Jednadžba y=x 2 -16 ima dva korijena, a oba leže u kompleksnoj ravnini: x 1 =4i, x 2 =-4i.

Uobičajene pogreške

Česta pogreška školaraca koji još nisu shvatili što su nule funkcije je zamjena argumenta (x) nulom, a ne vrijednosti (y) funkcije. Oni pouzdano zamjenjuju x = 0 u jednadžbu i na temelju toga pronalaze y. Ali ovo je pogrešan pristup.

Druga je pogreška, kao što je već spomenuto, redukcija sinusom ili kosinusom u trigonometrijskoj jednadžbi, zbog čega se gubi jedna ili više nula funkcije. To ne znači da se u takvim jednadžbama ništa ne može reducirati, ali se ti „izgubljeni“ faktori moraju uzeti u obzir u daljnjim izračunima.

Grafički prikaz

Možete razumjeti što su nule funkcije uz pomoć matematičkih programa kao što je Maple. U njemu možete izgraditi graf navodeći željeni broj točaka i željenu ljestvicu. One točke u kojima graf prelazi os OX su željene nule. Ovo je jedan od najbržih načina za pronalaženje korijena polinoma, pogotovo ako je njegov red veći od trećeg. Dakle, ako postoji potreba za redovitim izvođenjem matematičkih izračuna, pronalaženjem korijena polinoma proizvoljnih stupnjeva, građenjem grafova, Maple ili sličan program će biti jednostavno neophodan za izvođenje i provjeru izračuna.

Matematički prikaz funkcije jasno pokazuje kako jedna veličina u potpunosti određuje vrijednost druge veličine. Tradicionalno se smatraju numeričke funkcije koje povezuju jedan broj s drugim. Nula funkcije obično se naziva vrijednošću argumenta na kojoj funkcija nestaje.

Uputa

1. Da biste pronašli nule funkcije, trebate njezinu desnu stranu izjednačiti s nulom i riješiti rezultirajuću jednadžbu. Zamislite da vam je dana funkcija f(x)=x-5.

2. Da bismo pronašli nule ove funkcije, uzmimo i izjednačimo njezinu desnu stranu s nulom: x-5=0.

3. Rješavajući ovu jednadžbu, dobivamo da je x=5 i ta će vrijednost argumenta biti nula funkcije. To jest, kada je vrijednost argumenta 5, funkcija f(x) nestaje.

Pod podnošenjem funkcije u matematici razumjeti odnos između elemenata skupova. Točnije rečeno, to je “zakon” prema kojem se cijelom elementu jednog skupa (koji se naziva domena definicije) dodjeljuje određeni element drugog skupa (koji se naziva domena vrijednosti).

Trebat će vam

• Znanje iz algebre i matematički pregled.

Uputa

1. vrijednosti funkcije ovo je određeno područje iz kojeg funkcija može uzimati vrijednosti. Recimo raspon funkcije f(x)=|x| od 0 do beskonačnosti. Otkriti značenje funkcije u određenom trenutku, morate zamijeniti argument funkcije njegov numerički ekvivalent, rezultirajući broj će biti značenje m funkcije. Neka je funkcija f(x)=|x| – 10 + 4x. otkriti značenje funkcije u točki x=-2. Zamijenite broj -2 umjesto x: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. tj značenje funkcije u točki -2 je -16.

Bilješka!
Prije traženja vrijednosti funkcije u točki, provjerite je li uključena u opseg funkcije.

Koristan savjet
Sličnom metodom moguće je pronaći vrijednost funkcije nekoliko argumenata. Razlika je u tome što ćete umjesto jednog broja morati zamijeniti nekoliko - prema broju argumenata funkcije.

Funkcija je uspostavljeni odnos varijable y prema varijable x. Štoviše, cijela vrijednost x, nazvana argument, odgovara iznimnoj vrijednosti y - funkciji. U grafičkom obliku, funkcija je prikazana u kartezijanskom koordinatnom sustavu u obliku grafa. Točke presjeka grafa s apscisnom osi, na kojima su ucrtani argumenti x, nazivaju se nulama funkcije. Pronalaženje valjanih nula jedan je od zadataka pronalaženja zadane funkcije. U ovom slučaju se uzimaju u obzir sve dopuštene vrijednosti nezavisne varijable x koje čine domenu definicije funkcije (OOF).

Uputa

1. Nula funkcije je vrijednost argumenta x, na kojoj je vrijednost funkcije nula. Međutim, samo oni argumenti koji su uključeni u domenu definicije funkcije koja se proučava mogu biti nule. Odnosno, u tako puno vrijednosti za koje funkcija f (x) ima smisla.

2. Zapišite zadanu funkciju i izjednačite je s nulom, recimo f(x) = 2x?+5x+2 = 0. Riješite rezultirajuću jednadžbu i pronađite njezine stvarne korijene. Korijeni kvadratne jednadžbe izračunavaju se uz potporu pronalaženja diskriminanta. 2x? + 5x + 2 \u003d 0; D = b? -4ac = 5? -4 * 2 * 2 = 9; x1 = (-b +? D) / 2 * a = (-5 + 3) / 2 * 2 \u003d -0,5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2. Dakle, u ovom slučaju, dva dobivaju se korijeni kvadratne jednadžbe, koji odgovaraju argumentima početne funkcije f(x).

3. Provjerite pripadaju li sve otkrivene x vrijednosti domeni definicije zadane funkcije. Otkrijte OOF, da biste to učinili, provjerite početni izraz za prisutnost korijena parnog stupnja oblika? f (x), za prisutnost razlomaka u funkciji s argumentom u nazivniku, za prisutnost logaritamskih ili trigonometrijski izrazi.

4. Kada razmatrate funkciju s izrazom pod korijenom parnog stupnja, uzmite za područje definicije sve argumente x čije vrijednosti ne pretvaraju korijenski izraz u negativan broj (naprotiv, funkcija čini nema smisla). Navedite spadaju li otkrivene nule funkcije unutar određenog raspona prihvatljivih vrijednosti x.

5. Nazivnik razlomka ne može nestati, stoga isključite one argumente x koji dovode do takvog rezultata. Za logaritamske veličine treba uzeti u obzir samo one vrijednosti argumenta za koje je sam izraz veći od nule. Nule funkcije koje pretvaraju sublogaritamski izraz u nulu ili negativan broj moraju se odbaciti iz konačnog rezultata.

Bilješka!
Prilikom pronalaženja korijena jednadžbe mogu se pojaviti dodatni korijeni. To je lako provjeriti: dovoljno je dobivenu vrijednost argumenta zamijeniti u funkciju i osigurati da funkcija nestane.

Koristan savjet
Ponekad funkcija nije eksplicitno izražena kroz svoj argument, tada je lako znati što je funkcija. Primjer za to je jednadžba kružnice.