Nuly funkce dle rozpisu. Funkce nula. Pravidlo nulové funkce

Funkce je jedním z nejdůležitějších matematických pojmů. Funkce - proměnná závislost v z proměnné X, pokud každá hodnota X odpovídá jedné hodnotě v. variabilní X nazývaná nezávislá proměnná nebo argument. variabilní v nazývaná závislá proměnná. Všechny hodnoty nezávislé proměnné (proměnná X) tvoří definiční obor funkce. Všechny hodnoty, které nabývá závislá proměnná (proměnná y), tvoří rozsah funkce.

Funkční graf nazývají množinu všech bodů souřadnicové roviny, jejichž úsečky se rovnají hodnotám argumentu a pořadnice se rovnají odpovídajícím hodnotám funkce, tedy hodnotám proměnné jsou vyneseny podél osy x X a hodnoty proměnné jsou vyneseny podél osy y y. Chcete-li vykreslit funkci, musíte znát vlastnosti funkce. Hlavní vlastnosti funkce budou diskutovány níže!

Pro vykreslení funkčního grafu doporučujeme použít náš program - Graphing Functions Online. Máte-li nějaké dotazy při studiu materiálu na této stránce, můžete je kdykoli položit na našem fóru. Také na fóru vám pomůžeme řešit problémy z matematiky, chemie, geometrie, teorie pravděpodobnosti a mnoha dalších předmětů!

Základní vlastnosti funkcí.

1) Rozsah funkcí a rozsah funkcí.

Rozsah funkce je množina všech platných hodnot argumentu X(proměnná X), pro které je funkce y = f(x) definovaný.
Rozsah funkce je množina všech reálných hodnot yže funkce přijímá.

V elementární matematice se funkce studují pouze na množině reálných čísel.

2) Funkční nuly.

Nula funkce je hodnota argumentu, při které je hodnota funkce rovna nule.

3) Intervaly znaménkové stálosti funkce.

Intervaly konstantního znaménka funkce jsou takové sady hodnot argumentů, na kterých jsou hodnoty funkce pouze kladné nebo pouze záporné.

4) Monotonie funkce.

Rostoucí funkce (v nějakém intervalu) - funkce, ve které větší hodnota argumentu z tohoto intervalu odpovídá větší hodnotě funkce.

Klesající funkce (v nějakém intervalu) - funkce, ve které větší hodnota argumentu z tohoto intervalu odpovídá menší hodnotě funkce.

5) Sudé (liché) funkce.

Sudá funkce je funkce, jejíž definiční obor je symetrický vzhledem k počátku a pro libovolný X z oblasti definice rovnost f(-x) = f(x). Graf sudé funkce je symetrický podle osy y.

Lichá funkce je funkce, jejíž definiční obor je symetrický vzhledem k počátku a pro libovolný X z oblasti definice rovnost f(-x) = - f(x). Graf liché funkce je symetrický podle počátku.

6) Omezené a neomezené funkce.

Funkce se nazývá omezená, pokud existuje kladné číslo M takové, že |f(x)| ≤ M pro všechny hodnoty x . Pokud takové číslo neexistuje, pak je funkce neomezená.

7) Periodicita funkce.

Funkce f(x) je periodická, pokud existuje nenulové číslo T takové, že pro libovolné x f(x+T) = f(x). Toto nejmenší číslo se nazývá perioda funkce. Všechny goniometrické funkce jsou periodické. (Trigonometrické vzorce).

Po prostudování těchto vlastností funkce můžete funkci snadno prozkoumat a pomocí vlastností funkce vykreslit graf funkce. Podívejte se také na látku o pravdivostní tabulce, násobilce, periodické tabulce, tabulce derivací a integrální tabulce.

Funkce nuly

Co jsou funkční nuly? Jak určit nuly funkce analyticky a graficky?

Funkce nuly jsou hodnoty argumentu, při kterých je funkce rovna nule.

Abychom našli nuly funkce dané vzorcem y=f(x), musíme vyřešit rovnici f(x)=0.

Pokud rovnice nemá kořeny, pak funkce nemá nuly.

1) Najděte nuly lineární funkce y=3x+15.

Abychom našli nuly funkce, řešíme rovnici 3x+15 =0.

Nula funkce je tedy y=3x+15 - x= -5 .

2) Najděte nuly kvadratické funkce f(x)=x²-7x+12.

Abychom našli nuly funkce, řešíme kvadratickou rovnici

Její kořeny x1=3 a x2=4 jsou nuly této funkce.

3) Najděte nuly funkce

Zlomek má smysl, pokud je jmenovatel jiný než nula. Proto x²-1≠0, x² ≠ 1,x ≠±1. To znamená, že doména definice této funkce (ODZ)

Z kořenů rovnice x²+5x+4=0 x1=-1 x2=-4 je do definičního oboru zahrnuto pouze x=-4.

Pro nalezení nul graficky zadané funkce je nutné najít průsečíky grafu funkce s osou x.

Pokud graf neprotíná osu Ox, funkce nemá žádné nuly.

funkce, jejíž graf je na obrázku, má čtyři nuly -

V algebře se problém hledání nul funkce vyskytuje jak jako samostatná úloha, tak při řešení jiných problémů, například při studiu funkce, řešení nerovnic atd.

www.algebraclass.ru

Pravidlo nulové funkce

Základní pojmy a vlastnosti funkcí

pravidlo (zákon) shody. Monotónní funkce .

Omezené a neomezené funkce. Průběžné a

diskontinuální funkce . Sudé a liché funkce.

Periodická funkce. Funkční období.

Funkce nuly . Asymptota .

Rozsah a rozsah funkce. V elementární matematice se funkce studují pouze na množině reálných čísel R . To znamená, že argument funkce může nabývat pouze těch skutečných hodnot, pro které je funkce definována, tj. přijímá také pouze skutečné hodnoty. Hodně X všechny platné platné hodnoty argumentu X, pro které je funkce y = F (X) je definován, tzv rozsah funkce. Hodně Y všechny skutečné hodnoty yže funkce přijímá se volá funkční rozsah. Nyní můžeme uvést přesnější definici funkce: pravidlo (zákon) korespondence mezi množinami X A Y , kterým pro každý prvek ze sady X můžete najít jeden a pouze jeden prvek ze sady Y, se nazývá funkce .

Z této definice vyplývá, že funkce je považována za danou, pokud:

- je nastaven rozsah funkce X ;

— je nastaven rozsah funkčních hodnot Y ;

- je známo pravidlo (zákon) korespondence, a to takové, že pro každou

argument hodnoty, lze nalézt pouze jednu funkční hodnotu.

Tento požadavek jedinečnosti funkce je povinný.

monotónní funkce. Pokud pro libovolné dvě hodnoty argumentu X 1 a X 2 podmínky X 2 > X 1 následuje F (X 2) > F (X 1), pak funkce F (X) je nazýván vzrůstající; pokud pro nějaké X 1 a X 2 podmínky X 2 > X 1 následuje F (X 2)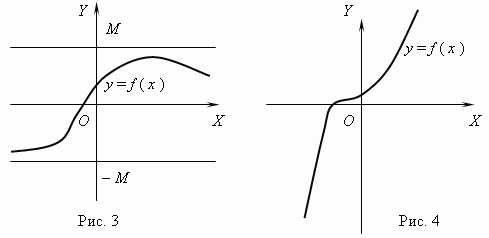

Funkce znázorněná na obr. 3 je omezená, ale není monotónní. Funkce na obrázku 4 je přesně opačná, monotónní, ale neomezená. (Vysvětlete to prosím!)

Spojité a nespojité funkce. Funkce y = F (X) je nazýván kontinuální na místě X = A, pokud:

1) funkce je definována pro X = A, tj. F (A) existuje;

2) existuje konečný limit lim F (X) ;

Pokud není splněna alespoň jedna z těchto podmínek, je funkce volána nespojitý na místě X = A .

Pokud je funkce spojitá v Všechno body své domény definice, pak se to nazývá spojitá funkce.

Sudé a liché funkce. Pokud pro žádný X z rozsahu definice funkce se odehrává: F (— X) = F (X), pak se zavolá funkce dokonce; pokud ano: F (— X) = — F (X), pak se zavolá funkce zvláštní. Graf sudé funkce symetricky podle osy Y(obr.5), graf liché funkce Sim metrika o původu(obr. 6).

Periodická funkce. Funkce F (X) — časopis pokud takový existuje nenulovéčíslo T k čemu žádný X z rozsahu definice funkce se odehrává: F (X + T) = F (X). Takový nejméněčíslo se volá funkční období. Všechny goniometrické funkce jsou periodické.

PŘÍKLAD 1. Dokažte ten hřích X má období 2.

ŘEŠENÍ Víme, že hřích ( x + 2 n) = hřích X, kde n= 0, ± 1, ± 2, …

Proto přidání 2 n k sinusovému argumentu

mění svou hodnotu e . Existuje další číslo s tímto?

Předstírejme to P- takové číslo, tj. rovnost:

platný pro jakoukoli hodnotu X. Ale pak má

místo a na X= / 2, tj.

hřích (/2 + P) = hřích / 2 = 1.

Ale podle redukčního vzorce sin (/ 2 + P) = cos P. Pak

z posledních dvou rovností vyplývá, že cos P= 1, ale my

Víme, že to platí pouze pro P = 2 n. Od nejmenšího

nenulové číslo ze 2 n je 2, pak toto číslo

a je tu dobový hřích X. Podobně je dokázáno, že 2

je období pro cos X .

Dokažte, že funkce tan X a kočka X mít období.

Příklad 2. Jaké číslo je perioda funkce sin 2 X ?

Řešení. Zvažte hřích 2 X= hřích (2 x + 2 n) = hřích [ 2 ( X + n) ] .

Vidíme to přidání n k argumentu X, se nemění

funkční hodnotu. Nejmenší nenulové číslo

z n je , takže toto je období sin 2 X .

Nuly funkce. Zavolá se hodnota argumentu, pro který je funkce rovna 0 nula ( kořenové) funkce. Funkce může mít více nul. Například funkce y = X (X + 1) (X- 3) má tři nuly: X = 0, X = — 1, X= 3. Geometricky funkce null – je úsečka průsečíku grafu funkce s osou X .

Obrázek 7 ukazuje graf funkce s nulami: X = A , X = b A X = C .

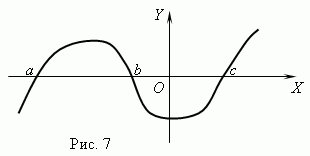
Asymptota. Pokud se graf funkce neomezeně přibližuje k určité přímce, jak se vzdaluje od počátku, pak se tato přímka nazývá asymptota.

Téma 6. "Metoda intervalů".

Jestliže f (x) f (x 0) pro x x 0, pak je volána funkce f (x). spojitý při x 0.

Pokud je funkce spojitá v každém bodě nějakého intervalu I, pak je volána kontinuálně na intervalu I (interval I se nazývá interval kontinuity funkce). Grafem funkce na tomto intervalu je souvislá čára, o které se říká, že je „kreslena bez zvednutí tužky z papíru“.

Vlastnost spojitých funkcí.

Pokud je na intervalu (a ; b) funkce f spojitá a nezaniká, pak si na tomto intervalu zachovává konstantní znaménko.

Na této vlastnosti je založena metoda řešení nerovnic s jednou proměnnou - metoda intervalů. Nechť je funkce f(x) spojitá na intervalu I a zaniká v konečném počtu bodů v tomto intervalu. Vlastností spojitých funkcí tyto body rozdělují I na intervaly, v každém z nich spojitá funkce f(x) c střeží konstantní znaménko. K určení tohoto znaménka stačí vypočítat hodnotu funkce f(x) v libovolném bodě z každého takového intervalu. Na základě toho získáme následující algoritmus pro řešení nerovnic intervalovou metodou.

Intervalová metoda pro nerovnice tvaru

Najděte definiční obor funkce f(x) ;

Najděte nuly funkce f(x) ;

Nakreslete na číselnou osu definiční obor a nuly funkce. Nuly funkce rozdělují její definiční obor na intervaly, v každém z nich si funkce zachovává konstantní znaménko;

Najděte znaménka funkce v získaných intervalech výpočtem hodnoty funkce v libovolném bodě z každého intervalu;

Zapište odpověď.

intervalová metoda. Průměrná úroveň.

Chcete si otestovat své síly a zjistit výsledek, jak jste připraveni na Jednotnou státní zkoušku nebo OGE?

Lineární funkce

Funkce tvaru se nazývá lineární. Vezměme si jako příklad funkci. Je kladná na 3″> a záporná na. Bod je nula funkce (). Ukažme si znaky této funkce na reálné ose:

Říkáme, že "funkce při průchodu bodem změní znaménko".

Je vidět, že znaménka funkce odpovídají poloze grafu funkce: pokud je graf nad osou, je znaménko „ “, pokud je pod ní „ “.

Pokud výsledné pravidlo zobecníme na libovolnou lineární funkci, dostaneme následující algoritmus:

Najdeme nulu funkce;

Označíme jej na číselné ose;

Určíme znaménko funkce na opačných stranách nuly.

kvadratická funkce

Doufám, že si pamatujete, jak se řeší kvadratické nerovnosti? Pokud ne, přečtěte si téma "Čtvercové nerovnosti". Dovolte mi připomenout obecný tvar kvadratické funkce: .

Nyní si připomeňme, jaká znamení má kvadratická funkce. Jeho graf je parabola a funkce má znaménko „ “ pro ty, ve kterých je parabola nad osou, a „ “ - pokud je parabola pod osou:

Pokud má funkce nuly (hodnoty při kterých), parabola protíná osu ve dvou bodech - kořenech odpovídající kvadratické rovnice. Osa je tedy rozdělena na tři intervaly a znaménka funkce se při průchodu každým kořenem střídavě mění.

Je možné nějak určit znaménka, aniž bychom pokaždé nakreslili parabolu?

Připomeňme, že čtvercový trojčlen lze faktorizovat:

Všimněte si kořenů na ose:

Pamatujeme si, že znaménko funkce se může změnit pouze při průchodu kořenem. Využíváme toho: pro každý ze tří intervalů, na které je osa rozdělena kořeny, stačí určit znaménko funkce pouze v jednom libovolně zvoleném bodě: v ostatních bodech intervalu bude znaménko stejný.

V našem příkladu: pro 3″> jsou oba výrazy v závorkách kladné (dosadíme např.: 0″>). Na osu dáme znak "":

Pokud jsou (například náhrada) obě závorky záporné, pak je součin kladný:

Tak to je intervalová metoda: když známe znaménka faktorů na každém intervalu, určíme znaménko celého produktu.

Uvažujme i případy, kdy funkce nemá nuly nebo je pouze jedna.

Pokud nejsou žádné, pak nejsou žádné kořeny. To znamená, že nedojde k žádnému „průchodu kořenem“. To znamená, že funkce na celé číselné ose má pouze jedno znaménko. Je snadné jej určit dosazením do funkce.

Pokud je kořen pouze jeden, parabola se dotýká osy, takže znaménko funkce se při průchodu kořenem nemění. Jaké je pravidlo pro takové situace?

Pokud takovou funkci vyloučíme, dostaneme dva stejné faktory:

A jakýkoli čtvercový výraz je nezáporný! Znaménko funkce se tedy nemění. V takových případech vybereme kořen, při průchodu kterým se znaménko nemění, a zakroužíme jej čtvercem:

Takový kořen se bude nazývat násobek.

Metoda intervalů v nerovnicích

Nyní lze jakoukoli kvadratickou nerovnost vyřešit bez kreslení paraboly. Stačí umístit znaménka kvadratické funkce na osu a zvolit intervaly v závislosti na znaménku nerovnosti. Například:

Změříme kořeny na ose a uspořádáme značky:

Potřebujeme část osy se znaménkem ""; protože nerovnost není striktní, jsou do řešení zahrnuty i samotné kořeny:

Nyní uvažujme racionální nerovnost - nerovnost, jejíž obě části jsou racionálními výrazy (viz "Racionální rovnice").

Příklad:

Všechny faktory kromě jednoho - - zde jsou "lineární", to znamená, že obsahují proměnnou pouze v prvním stupni. Takové lineární faktory potřebujeme k aplikaci intervalové metody - znaménko se mění při průchodu jejich kořeny. Ale multiplikátor nemá vůbec žádné kořeny. To znamená, že je vždy kladný (sami si to ověřte), a neovlivňuje tedy znaménko celé nerovnosti. To znamená, že na ni můžete rozdělit levou a pravou stranu nerovnosti a tím se jí zbavit:

Nyní je vše stejné jako u kvadratických nerovností: určíme, ve kterých bodech každý z faktorů mizí, označíme tyto body na ose a uspořádáme znaménka. Upozorňuji na velmi důležitou skutečnost:

V případě sudého čísla postupujeme stejně jako dříve: bod okroužíme čtvercem a při průchodu odmocninou neměníme znaménko. Ale v případě lichého čísla toto pravidlo není splněno: znaménko se při průchodu kořenem stejně změní. S takovým kořenem tedy dodatečně nic neděláme, jako by to nebyl náš násobek. Výše uvedená pravidla platí pro všechny sudé a liché mocniny.

Co napíšeme do odpovědi?

Pokud dojde k porušení střídání znaků, musíte být velmi opatrní, protože při nepřísné nerovnosti by odpověď měla zahrnovat všechny vyplněné body. Některé z nich ale často stojí osamoceně, to znamená, že nevstupují do zastíněného prostoru. V tomto případě je přidáme do odpovědi jako izolované tečky (ve složených závorkách):

Příklady (rozhodněte se sami):

Odpovědi:

1. Pokud je mezi faktory jednoduchý - toto je kořen, protože to může být reprezentováno jako.
   .

kde nabývá hodnoty nula. Například pro funkci danou vzorcem

je nulový, protože

.

Volají se také funkce nuly kořeny funkcí.

Koncept nul funkce může být uvažován pro všechny funkce, jejichž rozsah obsahuje nulu nebo nulový prvek odpovídající algebraické struktury.

Pro funkci reálné proměnné jsou nuly hodnoty, ve kterých graf funkce protíná osu x.

Hledání nul funkce často vyžaduje použití numerických metod (například Newtonova metoda, gradientní metody).

Jedním z nevyřešených matematických problémů je hledání nul Riemannovy zeta funkce.

Polynomiální kořen

viz také

Literatura

Nadace Wikimedia. 2010

Podívejte se, co je "Function Zero" v jiných slovnících:

Bod, kde daná funkce f(z) zmizí; tedy N. f. f (z) je stejné jako kořeny rovnice f (z) = 0. Například body 0, π, π, 2π, 2π,... jsou nuly funkce sinz. Nuly analytické funkce (viz Analytické ... ...

Nulová funkce, nulová funkce... Pravopisný slovník

Tento výraz má jiné významy, viz nula. Je nutné přesunout obsah tohoto článku do článku "Function Zero". Projektu můžete pomoci konsolidací článků. Pokud potřebujete diskutovat o vhodnosti sloučení, nahraďte toto ... Wikipedie

Nebo řetězec C (z názvu jazyka C) nebo řetězec ASCIZ (z názvu direktivy assembleru.asciz) je způsob reprezentace řetězců v programovacích jazycích, ve kterém se místo vložení znaku používá pole znaků. speciální typ řetězce a konec ... ... Wikipedie

V kvantové teorii pole přijatý (slangový) název pro vlastnost mizení renormalizačního faktoru vazebné konstanty, kde g0 je holá vazebná konstanta z interakce Lagrangian, phys. spojovací konstanta upravená interakcí. Rovnost Z... Fyzická encyklopedie

Nulová mutace n-alela- Nulová mutace, n. alela * nulová mutace, n. alela * nulová mutace nebo n. alela nebo tichá a. mutace vedoucí k úplné ztrátě funkce v sekvenci DNA, ve které k ní došlo... Genetika. encyklopedický slovník

Tvrzení v teorii pravděpodobnosti, že jakákoli událost (tzv. zbytková událost), jejíž výskyt je dán pouze libovolně vzdálenými prvky posloupnosti nezávislých náhodných událostí nebo náhodných proměnných, má ... ... Matematická encyklopedie

1) Číslo, které má tu vlastnost, že žádné (reálné nebo komplexní) číslo se po přidání nezmění. Označuje se symbolem 0. Součin libovolného čísla N. je roven N.: Je-li součin dvou čísel roven N., pak jeden z faktorů ... Matematická encyklopedie

Funkce dané vztahy mezi nezávislými proměnnými, které nejsou vyřešeny s ohledem na druhé; tyto vztahy jsou jedním ze způsobů, jak definovat funkci. Například vztah x2 + y2 1 = 0 definuje N. f. … Velká sovětská encyklopedie

Hodnoty argumentu z pod kterými F(z) přejde na nulu. nulový bod, tj. -li F(A) = 0 tedy a - nulový bod.

Def. Tečka ale volala objednávka nulan , pokud FKP může být zastoupen ve formě F(z) = , kde
analytická funkce a
0.

V tomto případě, v rozšíření funkce v Taylorově řadě (43), první n koeficienty jsou nulové

= =

Atd. Určete řád nuly pro
a (1-cos z) v z = 0

=
=

nula 1. řádu

1 - cos z =
=

nula 2. řádu

Def. Tečka z =
volala bod v nekonečnu A nula funkcí F(z), pokud F(
) = 0. Taková funkce expanduje do řady v záporných mocninách z : F(z) =
. Li za prvé n koeficienty se rovnají nule, pak dospějeme k nulový řád n v bodě v nekonečnu: F(z) = z - n
.

Izolované singulární body se dělí na: a) odnímatelné singulární body; b) řádové sloupyn; v) podstatné singulární body.

Tečka ale volala odnímatelný singulární bod funkcí F(z) pokud z
A lim F(z) = z - konečné číslo .

Tečka ale volala pól řádun (n 1) vlastnosti F(z) v případě inverzní funkce
= 1/ F(z) má pořadí nula n na místě ale. Taková funkce může být vždy reprezentována jako F(z) =
, kde
- analytická funkce a
.

Tečka ale volala podstatný bod funkcí F(z), pokud z
A lim F(z) neexistuje.

série Laurent

Zvažte případ prstencové konvergenční oblasti r < | z 0 – A| < R soustředěný na bod ale pro funkci F(z). Představujeme dva nové kruhy L 1 (r) A L 2 (R) v blízkosti hranic prstence s tečkou z 0 mezi nimi. Udělejme řez prstenu, spojíme kruhy podél okrajů řezu, přejdeme do jednoduše spojené oblasti a v

Cauchyův integrální vzorec (39) získáme dva integrály nad proměnnou z

F(z 0) =
+
, (42)

kde integrace jde opačným směrem.

Pro integrál přes L 1 podmínka | z 0 – A | > | z – A |, a pro integrál přes L 2 obrácený stav | z 0 – A | < | z – A |. Proto faktor 1/( z – z 0) expandovat v řadě (a) v integrálu přes L 2 a v řadě (b) v integrálním over L jeden . V důsledku toho dostaneme rozklad F(z) v prstencové oblasti v série Laurent v pozitivních a negativních silách ( z 0 – A)

F(z 0) =
A n (z 0 – a) n (43)

kde A n =
=
;A -n =

Rozšíření pozitivních sil (z 0 - ale) volala pravá část Laurentova série (série Taylor) a expanze záporných sil se nazývá. hlavní část Laurent řada.

Pokud uvnitř kruhu L 1 nejsou žádné singulární body a funkce je analytická, pak v (44) je první integrál roven nule podle Cauchyho věty a v rozšíření funkce zůstává pouze správná část. Záporné mocniny v expanzi (45) se objevují pouze tehdy, když je analyticita narušena uvnitř vnitřního kruhu a slouží k popisu funkce v blízkosti izolovaných singulárních bodů.

Ke konstrukci Laurentovy řady (45) pro F(z) lze vypočítat expanzní koeficienty podle obecného vzorce nebo použít expanze elementárních funkcí obsažených v F(z).

Počet termínů ( n) hlavní části Laurentovy řady závisí na typu singulárního bodu: odnímatelný singulární bod (n = 0) ; podstatný singulární bod (n
); póln-tý řád(n - koncové číslo).

a pro F(z) = tečka z = 0 odnímatelný singulární bod, protože není tam žádná hlavní část. F(z) = (z -
) = 1 -

b) Pro F(z) = tečka z = 0 - pól 1. řádu

F(z) = (z -
) = -

c) Pro F(z) = E 1 / z tečka z = 0 - podstatný singulární bod

F(z) = E 1 / z =

Li F(z) je v doméně analytický D s výjimkou m izolované singulární body a | z 1 | < |z 2 | < . . . < |z m| , pak při rozšiřování funkce v mocninách z celá rovina je rozdělena na m+ 1 prsten | z i | < | z | < | z i+ 1 | a Laurentova řada má pro každý prsten jinou podobu. Při rozšiřování pravomocí ( z – z i ) oblast konvergence Laurentovy řady je kružnice | z – z i | < r, kde r je vzdálenost k nejbližšímu singulárnímu bodu.

Atd. Rozbalte funkci F(z) =v Laurentově sérii v mocnostech z A ( z - 1).

Řešení. Funkci reprezentujeme ve tvaru F(z) = - z 2 . Použijeme vzorec pro součet geometrické posloupnosti
. V kruhu |z|< 1 ряд сходится и F(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4 - . . . , tj. rozklad obsahuje pouze opravitčást. Přesuňme se do vnější oblasti kruhu |z| > 1. Funkci reprezentujeme ve tvaru
, kde 1/| z| < 1, и получим разложение F(z) = z
=z + 1 +

Protože , rozšíření funkce v mocninách ( z - 1) vypadá F(z) = (z - 1) -1 + 2 + (z - 1) pro všechny
1.

Atd. Rozšiřte funkci v Laurentově řadě F(z) =
: a) ve stupních z v kruhu | z| < 1; b) по степеням z prsten 1< |z| < 3 ; c) по степеням (z – 2).Rozhodnutí. Pojďme si funkci rozložit na jednoduché zlomky
= =+=
. Z podmínek z =1
A = -1/2 , z =3
B = ½.

ale) F(z) = ½ [
] = ½ [
-(1/3)
], když | z|< 1.

b) F(z) = - ½ [
+
] = - (
), v 1< |z| < 3.

z) F(z) = ½ [
]= - ½ [
] =

= - ½ = -
, pro |2 - z| < 1

Je to kružnice o poloměru 1 se středem v bodě z = 2 .

V některých případech lze mocninné řady redukovat na sadu geometrických progresí a pak je snadné určit oblast jejich konvergence.

Atd. Prozkoumejte konvergenci řady

. . . + + + + 1 + () + () 2 + () 3 + . . .

Řešení. Je to součet dvou geometrických posloupností s q 1 = , q 2 = () . Z podmínek jejich konvergence to vyplývá < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

Co jsou funkční nuly? Odpověď je celkem jednoduchá – jde o matematický pojem, který znamená definiční obor dané funkce, na kterém je její hodnota nula. Funkční nuly se také nazývají Funkční nuly Nejjednodušší způsob, jak vysvětlit, co jsou funkční nuly, je na několika jednoduchých příkladech.

Příklady

Uvažujme jednoduchou rovnici y=x+3. Protože nula funkce je hodnotou argumentu, ve kterém se y stalo nulou, dosadíme 0 na levou stranu rovnice:

V tomto případě je -3 požadovaná nula. Pro danou funkci existuje pouze jeden kořen rovnice, ale není tomu tak vždy.

Zvažte další příklad:

Dosaďte 0 na levou stranu rovnice, jako v předchozím příkladu:

Je zřejmé, že v tomto případě budou ve funkci dvě nuly: x=3 a x=-3. Pokud by rovnice měla argument třetího stupně, byly by tři nuly. Můžeme učinit jednoduchý závěr, že počet kořenů polynomu odpovídá maximálnímu stupni argumentu v rovnici. Mnoho funkcí, například y=x 3 , však tomuto tvrzení na první pohled odporuje. Logika a zdravý rozum naznačují, že tato funkce má pouze jednu nulu – v bodě x=0. Ale ve skutečnosti existují tři kořeny, všechny se shodují. Pokud rovnici vyřešíte v komplexní formě, bude to zřejmé. x=0 v tomto případě kořen, jehož násobnost je 3. V předchozím příkladu se nuly neshodovaly, proto měly násobnost 1.

Definiční algoritmus

Z uvedených příkladů je zřejmé, jak určit nuly funkce. Algoritmus je vždy stejný:

1. Napište funkci.
2. Dosaďte y nebo f(x)=0.
3. Vyřešte výslednou rovnici.

Složitost poslední položky závisí na míře argumentu rovnice. Při řešení rovnic vysokých stupňů je zvláště důležité pamatovat na to, že počet kořenů rovnice se rovná maximální síle argumentu. To platí zejména pro goniometrické rovnice, kde dělení obou částí sinem nebo kosinus vede ke ztrátě kořenů.

Libovolné stupňové rovnice se nejsnáze řeší Hornerovou metodou, která byla vyvinuta speciálně pro hledání nul libovolného polynomu.

Hodnota nul funkcí může být záporná i kladná, skutečná nebo ležící v komplexní rovině, jednoduchá nebo násobná. Nebo tam nemusí být žádné kořeny rovnice. Například funkce y=8 se nestane nulou pro žádné x, protože na této proměnné nezávisí.

Rovnice y=x 2 -16 má dva kořeny a oba leží v komplexní rovině: x 1 =4i, x 2 =-4i.

Obyčejné chyby

Častou chybou školáků, kteří ještě pořádně nepřišli na to, jaké jsou nuly funkce, je nahrazení argumentu (x) nulou, a nikoli hodnotou (y) funkce. S jistotou dosadí do rovnice x = 0 a na základě toho najdou y. Ale to je špatný přístup.

Další chybou, jak již bylo zmíněno, je redukce o sinus nebo kosinus v goniometrické rovnici, proto dochází ke ztrátě jedné nebo více nul funkce. To neznamená, že v takových rovnicích nelze nic redukovat, ale tyto „ztracené“ faktory je třeba vzít v úvahu při dalších výpočtech.

Grafické znázornění

Co jsou nuly funkce, můžete pochopit pomocí matematických programů, jako je Maple. V něm můžete sestavit graf zadáním požadovaného počtu bodů a požadovaného měřítka. Body, ve kterých graf protíná osu OX, jsou požadované nuly. Toto je jeden z nejrychlejších způsobů, jak najít kořeny polynomu, zvláště pokud je jeho řád vyšší než třetí. Pokud je tedy potřeba pravidelně provádět matematické výpočty, hledat kořeny polynomů libovolných stupňů, sestavovat grafy, Maple nebo podobný program bude pro provádění a ověřování výpočtů prostě nepostradatelný.

Matematické znázornění funkce jasně ukazuje, jak jedna veličina zcela určuje hodnotu jiné veličiny. Tradičně jsou považovány za numerické funkce, které spojují jedno číslo s druhým. Nula funkce se obvykle nazývá hodnota argumentu, při kterém funkce zmizí.

Návod

1. Chcete-li najít nuly funkce, musíte porovnat její pravou stranu s nulou a vyřešit výslednou rovnici. Představte si, že máte funkci f(x)=x-5.

2. Abychom našli nuly této funkce, vezmeme a přirovnáme její pravou stranu k nule: x-5=0.

3. Řešením této rovnice dostaneme, že x=5 a tato hodnota argumentu bude nula funkce. To znamená, že když je hodnota argumentu 5, funkce f(x) zmizí.

Pod podáním funkcí v matematice rozumět vztahu mezi prvky množin. Přesněji řečeno, jde o „zákon“, podle kterého je celému prvku jedné množiny (nazývané definiční doména) přiřazen určitý prvek jiné množiny (nazývaná doména hodnot).

Budete potřebovat

• Znalosti v algebře a matematický přehled.

Návod

1. Hodnoty funkcí to je určitá oblast, ze které může funkce nabývat hodnot. Řekněme rozsah funkcí f(x)=|x| od 0 do nekonečna. Objevit význam funkcí v určitém bodě musíte argument nahradit funkcí jeho číselný ekvivalent, výsledné číslo bude význam m funkcí. Nechť funkci f(x)=|x| – 10 + 4x. objevit význam funkcí v bodě x=-2. Dosaďte místo x číslo -2: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Tj význam funkcí v bodě -2 je -16.

Poznámka!
Před hledáním hodnoty funkce v bodě se ujistěte, že je zahrnuta v rozsahu funkce.

Užitečná rada
Obdobnou metodou je možné zjistit hodnotu funkce více argumentů. Rozdíl je v tom, že místo jednoho čísla budete muset nahradit několik - podle počtu argumentů funkce.

Funkce je vytvořený vztah proměnné y z proměnné x. Navíc celá hodnota x, nazývaná argument, odpovídá výjimečné hodnotě y – funkci. V grafické podobě je funkce zobrazena na kartézském souřadnicovém systému ve formě grafu. Průsečíky grafu s osou úsečky, na kterých jsou vyneseny argumenty x, se nazývají nuly funkce. Hledání platných nul je jedním z úkolů hledání dané funkce. V tomto případě se berou v úvahu všechny přípustné hodnoty nezávislé proměnné x, které tvoří doménu definice funkce (OOF).

Návod

1. Nula funkce je hodnota argumentu x, při které je hodnota funkce nulová. Nuly však mohou být pouze ty argumenty, které jsou zahrnuty v oblasti definice studované funkce. To znamená, že v takovém množství hodnot, pro které má funkce f (x) smysl.

2. Zapište si danou funkci a přirovnejte ji k nule, řekněte f(x) = 2x?+5x+2 = 0. Vyřešte výslednou rovnici a najděte její skutečné kořeny. Kořeny kvadratické rovnice jsou vypočteny s podporou hledání diskriminantu. 2x? + 5x + 2 \u003d 0; D \u003d b? -4ac \u003d 5? -4 * 2 * 2 \u003d 9; x1 \u003d (-b +? D) / 2 * a \u003d (-5 + 3) / 2 * 2 \u003d -0,5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2. V tomto případě tedy dvě jsou získány kořeny kvadratické rovnice, odpovídající argumentům počáteční funkce f(x).

3. Zkontrolujte všechny zjištěné hodnoty x, zda patří do domény definice dané funkce. Detekujte OOF, za tímto účelem zkontrolujte počáteční výraz na přítomnost kořenů sudého stupně tvaru? f (x), na přítomnost zlomků ve funkci s argumentem ve jmenovateli, na přítomnost logaritmického nebo trigonometrické výrazy.

4. Při zvažování funkce s výrazem pod kořenem sudého stupně vezměte za definiční obor všechny argumenty x, jejichž hodnoty nemění kořenový výraz na záporné číslo (naopak funkce ano Nedává smysl). Určete, zda zjištěné nuly funkce spadají do určitého rozsahu přijatelných hodnot x.

5. Jmenovatel zlomku nemůže zmizet, proto vylučte ty argumenty x, které vedou k takovému výsledku. U logaritmických veličin je třeba uvažovat pouze ty hodnoty argumentu, pro které je samotný výraz větší než nula. Nuly funkcí, které mění sublogaritmický výraz na nulu nebo záporné číslo, musí být z konečného výsledku vyřazeny.

Poznámka!
Při hledání kořenů rovnice se mohou objevit další kořeny. Je snadné to zkontrolovat: stačí dosadit získanou hodnotu argumentu do funkce a ujistit se, že funkce zmizí.

Užitečná rada
Občas funkce není explicitně vyjádřena prostřednictvím svého argumentu, pak je snadné vědět, co je funkce. Příkladem toho je rovnice kruhu.