An example of calculating the beta distribution of a random variable. Beta distribution. Continuous distributions in MS EXCEL. An excerpt characterizing the Beta distribution
Consider the Beta distribution, calculate its mathematical expectation, variance, and mode. Using the MS EXCEL BETA.DIST () function, we will plot the graphs of the distribution function and probability density. Let's generate an array random numbers and estimate the distribution parameters.
Beta distributionBeta- distribution) depends on 2 parameters: α ( alpha)> 0(determines the shape of the distribution) and b (beta)> 0(determines the scale).
Unlike many other continuous distributions, the range of variation of a random variable having Beta distribution, is limited by the segment. Outside this segment distribution density equals 0. The boundaries of this segment are set by the researcher depending on the problem. If A = 0 and B = 1, then such Beta distribution called standard.
Beta distribution has the designation Beta(alpha; beta).
Note: If the parameters alpha and beta= 1, then Beta distribution turns into, i.e. Beta (1; 1; A; B) = U (A; B).
In general distribution function cannot be expressed in elementary functions, therefore it is calculated by numerical methods, for example, using the MS EXCEL BETA.DIST () function.
Note: For the convenience of writing formulas in the example file for the distribution parameters alpha and beta appropriate.
The example file also contains graphs probability density and distribution functions with marked values middle, and . 
Random number generation and parameter estimation
Using inverse distribution function(or quantile values ( p- quantile), see) you can generate values of a random variable having Beta distribution... To do this, you need to use the formula:
BETA.OBR (RAND (); alpha; beta; A; B)
ADVICE: Because random numbers are generated using the RAND () function, then pressing the key F9, it is possible to obtain a new sample each time and, accordingly, a new estimate of the parameters.
The RAND () function generates from 0 to 1, which exactly corresponds to the range of variation of the probability (see. example file sheet Generation).
Now having an array of random numbers generated with the given distribution parameters alpha and beta(let there be 200), let us estimate the distribution parameters.
Parameter estimation alpha and beta can be done with method of moments(it is assumed that parameters A and B are known): 
You are not a slave!
Closed educational course for children of the elite: "The true arrangement of the world."
http://noslave.org
From Wikipedia, the free encyclopedia
| Probability density Probability density function for the Beta distribution |
|
| Distribution function Cumulative distribution function for the Beta distribution |
|
| Designation | texvc not found; See math / README for setup help.): \ Text (Be) (\ alpha, \ beta)
|
| Options | Unable to parse expression (Executable texvc not found; See math / README - tuning reference.): \ Alpha> 0
Unable to parse expression (Executable texvc not found; See math / README for configuration help.): \ Beta> 0
|
| Carrier | Unable to parse expression (Executable texvc not found; See math / README for configuration help.): X \ in
|
| Probability density | Unable to parse expression (Executable texvc not found; See math / README for setup help.): \ Frac (x ^ (\ alpha-1) (1-x) ^ (\ beta-1)) (\ mathrm (B) (\ alpha, \ beta))
|
| Distribution function | Unable to parse expression (Executable texvc not found; See math / README for configuration help.): I_x (\ alpha, \ beta)
|
| Expected value | Unable to parse expression (Executable texvc not found; See math / README for tuning help.): \ Frac (\ alpha) (\ alpha + \ beta)
|
| Median | |
| Fashion | Unable to parse expression (Executable texvc not found; See math / README for tuning help.): \ Frac (\ alpha-1) (\ alpha + \ beta-2) for Unable to parse expression (Executable texvc not found; See math / README for tuning help.): \ Alpha> 1, \ beta> 1
|
| Dispersion | Unable to parse expression (Executable texvc not found; See math / README for setup help.): \ Frac (\ alpha \ beta) ((\ alpha + \ beta) ^ 2 (\ alpha + \ beta + 1))
|
| Asymmetry coefficient | Unable to parse expression (Executable texvc not found; See math / README for setup help.): \ Frac (2 \, (\ beta- \ alpha) \ sqrt (\ alpha + \ beta + 1)) ((\ alpha + \ beta + 2) \ sqrt (\ alpha \ beta))
|
| Kurtosis coefficient | Unable to parse expression (Executable texvc not found; See math / README for setup help.): 6 \, \ frac (\ alpha ^ 3- \ alpha ^ 2 (2 \ beta-1) + \ beta ^ 2 (\ beta + 1) -2 \ alpha \ beta (\ beta + 2)) (\ alpha \ beta (\ alpha + \ beta + 2) (\ alpha + \ beta + 3))
|
| Differential entropy | |
| Generating function of moments | Unable to parse expression (Executable texvc not found; See math / README for setup help.): 1 + \ sum_ (k = 1) ^ (\ infty) \ left (\ prod_ (r = 0) ^ (k-1) \ frac (\ alpha + r) (\ alpha + \ beta + r) \ right) \ frac (t ^ k) (k
!}
|
| Characteristic function | Unable to parse expression (Executable texvc not found; See math / README for setup help.): () _1F_1 (\ alpha; \ alpha + \ beta; i \, t)
|
Beta distribution in probability theory and statistics, a two-parameter family of absolutely continuous distributions. Used to describe random variables, the values of which are limited to a finite interval.
Definition
| 90px | Probability distributions | |
|---|---|---|
| One-dimensional | Multidimensional | |
| Discrete: | Bernoulli | Binomial | Geometric | Hypergeometric | Logarithmic | Negative binomial | Poisson | Discrete uniform | Multinomial |
| Absolutely continuous: | Beta| Weibulla | Gamma | Hyperexponential | Gompertz Distribution | Kolmogorov | Cauchy | Laplace | Lognormal | | | Kopula | |
An excerpt characterizing the Beta distribution
Tears glistened in my eyes ... And I was not at all ashamed of it. I would give a lot to meet one of them alive! .. Especially Magdalena. What wondrous, ancient Magic burned in the soul of this amazing woman when she created her magical kingdom ?! The kingdom in which Knowledge and Understanding ruled, and the backbone of which was Love. Only not the love that the “holy” church shouted about, having worn out this wondrous word to the point that I did not want to hear it any longer, but that beautiful and pure, real and courageous, the only and amazing LOVE with whose name the powers were born ... and with whose name the ancient warriors rushed into battle ... with whose name a new life was born ... by whose name our world changed and became better ... This Love was carried by the Golden Mary. And it is to this Mary that I would like to bow ... For everything that she carried, for her pure, bright LIFE, for her courage and courage, and for Love.But, unfortunately, it was impossible to do this ... She lived centuries ago. And I couldn't be the one who knew her. An incredibly deep, light sadness suddenly swept over my head, and bitter tears poured down ...
- Well, what are you, my friend! .. Other sorrows await you! - Sever exclaimed in surprise. - Please, calm down ...
He gently touched my hand and gradually the sadness disappeared. Only bitterness remained, as if I had lost something light and expensive ...
- You cannot relax ... War awaits you, Isidora.
- Tell me, Sever, was the teaching of the Cathars called the Teaching of Love because of the Magdalene?
- Here you are not quite right, Isidora. The uninitiated called him the Teaching of Love. For those who understood, it carried a completely different meaning. Listen to the sound of the words, Isidora: love in French sounds - amor - isn't it? And now, strip this word, separating the letter "a" from it ... It will turn out a'mor (a "mort) - without death ... This is the true meaning of the Magdalene's teachings - the Teaching of the Immortals. As I told you before - everything simply, Isidora, if only to look and listen correctly ... Well, and for those who do not hear - let it remain the Teaching of Love ... it is beautiful too.
I stood completely dumbfounded. The Teaching of the Immortals! .. Daariya ... So, what was the teaching of Radomir and Magdalene! .. The North surprised me many times, but never before I felt so shocked! .. The Teaching of the Cathars attracted me with its powerful, magical power, and I could not forgive myself for not talking about this with the North before.
- Tell me, Sever, is there anything left of the Qatar records? Something must have survived, right? Even if not the Perfect ones themselves, then at least just disciples? I mean something about their real life and teaching?
- Unfortunately - no, Isidora. The Inquisition destroyed everything, everywhere. Her vassals, by order of the Pope, were even sent to other countries to destroy every manuscript, every remaining piece of birch bark that they could find ... We were looking for at least something, but we could not save anything.
- Well, what about the people themselves? Couldn't there be something left for people who would keep it through the centuries?
- I don’t know, Isidora ... I think, even if someone had some kind of recording, it was changed over time. After all, it is natural for a person to reshape everything in his own way ... And especially without understanding. So it is unlikely that anything has survived as it was. It's a pity ... True, we have preserved the diaries of Radomir and Magdalene, but that was before the creation of the katar. Although, I think, the teaching has not changed.
- Sorry, for my confused thoughts and questions, Sever. I see that I have lost a lot without coming to you. But still, I'm still alive. And while I'm breathing, I can still ask you, can't I? Can you tell me how Svetodar's life ended? Sorry to interrupt.
Sever smiled sincerely. He liked my impatience and my thirst to "have time" to find out. And he continued with pleasure.
After his return, Svetodar lived and taught in Occitania for only two years, Isidora. But these years became the most expensive and happiest years of his wandering life. His days, illuminated by Beloyar's cheerful laughter, passed in his beloved Montsegur, surrounded by the Perfect ones, to whom Svetodar honestly and sincerely tried to convey what the distant Wanderer had taught him for many years.
- Bernoulli formula.
Itself distribution
are called binomial.
The parameters of the binomial distribution are the probability of success p (q = 1 - p) and the number of trials n. The binomial distribution is useful for describing the distribution of binomial events, such as the number of men and women in randomly selected companies. The use of the binomial distribution in game problems is of particular importance.
The exact formula for the probability m of successes in n trials is written as follows:
where p is the probability of success; q is 1-p, q> = 0, p + q = 1; n - number of tests, m = 0.1 ... m
The main characteristics of the binomial distribution:
6. Poisson's formula and Poisson distribution.
Let the number of trials n be large, the probability p small, and 
np is small. Then the probability of m successes in n trials can be approximately determined by Poisson's formula:
.
A random variable with a distribution series m, 
has a Poisson distribution. The more n, the more accurate the Poisson formula. For rough calculations, the formula is used for n = 10, 
0 - 2, for n = 100 
0 - 3. In engineering calculations, the formula is applied when n = 20, 
0 - 3, n = 100, 
0 - 7. For accurate calculations, the formula is applied when n = 100, 
0 - 7, n = 1000, 
0
– 15.
Let us calculate the mathematical expectation and variance of a random variable with a Poisson distribution.
The main characteristics of a Poisson random variable:
Poisson Distribution Plot:
7. Geometric distribution.
Consider the Bernoulli scheme. Let's designate X - the number of trials before the first success, if the probability of success in one trial is p. If the first test is successful, then X = 0. Therefore, 
... If X = 1, i.e. the first test is unsuccessful, and the second is successful, then by the multiplication theorem 
... Similarly, if X = n, then all tests up to the n-th test are unsuccessful and 
... Let's compose a series of distribution of a random variable X
|
|
| |||||
|
|
|
|
|
|
A random variable with such a distribution series has geometric distribution.
Let us check the normalization condition:
8. Hypergeometric distribution.
This is a discrete probability distribution of a random variable X taking integer values m = 0, 1,2, ..., n with probabilities:
where N, M and n are non-negative integers and M< N, n < N.
The mathematical expectation of the hypergeometric distribution does not depend on N and coincides with the mathematical expectation µ = np of the corresponding binomial distribution.
Dispersion of the hypergeometric distribution 
does not exceed the variance of the binomial distribution npq. Instances of any order of the hypergeometric distribution tend to the corresponding values of the moments of the binomial distribution.
9. Beta distribution.
The beta distribution has a density of the form:
The standard beta distribution is concentrated in the range from 0 to 1. Applying linear transformations, the beta value can be transformed so that it will take values at any range.
The main numerical characteristics of a quantity with a beta distribution:
The first, most natural step in probabilistic reasoning is as follows: if you have some variable that takes values at random, then you would like to know with what probabilities this variable takes on certain values. The combination of these probabilities is precisely what determines the probability distribution. For example, with a dice, you can a priori to assume that with equal probabilities 1/6 it will fall on any edge. And this happens under the condition that the bone is symmetrical. If the bone is asymmetric, then it is possible to determine high probabilities for those faces that fall out more often, and lower probabilities for those faces that fall out less often, based on experimental data. If some edge does not fall out at all, then it can be assigned a probability of 0. This is the simplest probability law that can be used to describe the results of throwing a dice. Of course, this is an extremely simple example, but similar problems arise, for example, in actuarial calculations, when real risk is calculated based on real data when issuing an insurance policy.
In this chapter, we will look at the most common probabilistic laws in practice.
These distributions can be easily plotted in STATISTICA.
Normal distribution
The normal probability distribution is especially commonly used in statistics. The normal distribution gives a good model for real-world phenomena in which:
1) there is a strong tendency for data to cluster around a center;
2) positive and negative deviations from the center are equally probable;
3) the frequency of deviations decreases rapidly when the deviations from the center become large.
The mechanism underlying the normal distribution, explained using the so-called central limit theorem, can be figuratively described as follows. Imagine you have pollen particles that you randomly tossed into a glass of water. Looking at an individual particle under a microscope, you will see an amazing phenomenon - the particle is moving. Of course, this happens because water molecules move and transfer their movement to particles of suspended pollen.
But how exactly does the movement take place? Here's a more interesting question. And this movement is very bizarre!
There are an infinite number of independent influences on an individual pollen particle in the form of impacts of water molecules, which cause the particle to move along a very strange trajectory. Under the microscope, this movement resembles a line repeatedly and chaotically broken. These kinks cannot be predicted, there is no regularity in them, which exactly corresponds to the chaotic collisions of molecules on a particle. A suspended particle, having experienced the impact of a water molecule at a random moment in time, changes its direction of motion, then moves for some time by inertia, then again falls under the impact of the next molecule, and so on. There is an amazing billiards table in a glass of water!
Since the movement of molecules has a random direction and speed, the magnitude and direction of the kinks in the trajectory are also completely random and unpredictable. This amazing phenomenon, called Brownian motion, discovered in the 19th century, makes us think about many things.
If we introduce a suitable system and mark the coordinates of the particle at some moments of time, then we will get the normal law. More precisely, the displacements of the pollen particle arising from the impact of molecules will obey the normal law.
For the first time, the law of motion of such a particle, called Brownian, was described at the physical level of rigor by A. Einstein. Then Lenjevan developed a simpler and more intuitive approach.
Twentieth-century mathematicians devoted their best pages to this theory, and the first step was taken 300 years ago, when the simplest version of the central limit theorem was discovered.
In probability theory, the central limit theorem, originally known in the formulation of Moivre and Laplace as early as the 17th century as a development of the famous law of large numbers by J. Bernoulli (1654-1705) (see J. Bernoulli (1713), Ars Conjectandi), is now extremely developed and reached its heights. in the modern principle of invariance, in the creation of which the Russian mathematical school played an essential role. It is in this principle that the motion of a Brownian particle finds its rigorous mathematical explanation.
The idea is that by summing up a large number of independent quantities (impacts of molecules on pollen particles) under certain reasonable conditions, it is precisely the normally distributed quantities that are obtained. And this happens independently, that is, invariantly, from the distribution of the initial values. In other words, if a variable is influenced by many factors, these influences are independent, relatively small and add up to each other, then the resulting value has a normal distribution.
For example, an almost infinite number of factors determine a person's weight (thousands of genes, predisposition, diseases, etc.). Thus, a normal distribution of weight in the population of all people can be expected.
If you are a financier and play on the stock exchange, then, of course, you are aware of cases when stock prices behave like Brownian particles, experiencing chaotic impacts of many factors.
Formally, the density of the normal distribution is written as follows:
where a and x 2 are the parameters of the law, interpreted, respectively, as the mean value and variance of a given random variable (due to the special role of the normal distribution, we will use special notation to denote its density function and distribution function). Visually, the normal density graph is the famous bell-shaped curve.
The corresponding distribution function of the normal random variable (a, x 2) is denoted by Ф (x; a, x 2) and is given by the relation:
A normal law with parameters a = 0 and x 2 = 1 is called standard.
Inverse standard normal distribution function applied to z, 0 Use the STATISTICA probabilistic calculator to calculate z from x and vice versa. Basic characteristics of the normal law: Average, mode, median: E = x mod = x med = a; Dispersion: D = х 2; Asymmetry: Excess: It can be seen from the formulas that the normal distribution is described by two parameters: a - mean - average; õ - stantard deviation - standard deviation, read: "sigma". Sometimes with the standard deviation is called the standard deviation, but this is already outdated terminology. Here are some useful facts about the normal distribution. The mean determines the measure of the density distribution. The normal distribution density is symmetric about the mean. The mean of the normal distribution coincides with the median and mode (see graphs). Normal distribution density with variance 1 and mean 1 Normal distribution density with mean 0 and variance 0.01 Normal distribution density with mean 0 and variance 4 With an increase in the variance, the density of the normal distribution spreads or spreads along the OX axis; with a decrease in the variance, it, on the contrary, contracts, concentrating around one point - the point of maximum value coinciding with the mean value. In the limiting case of zero variance, the random variable degenerates and takes on a single value equal to the mean. It is useful to know the 2- and 3-sigma, or 2- and 3-standard deviations, rules that are associated with the normal distribution and are used in a variety of applications. The meaning of these rules is very simple. If two and three standard deviations (2- and 3-sigma) are set to the right and left, respectively, from the point of the mean or, which is the same, from the point of maximum density of the normal distribution, then the area under the graph of normal density, calculated over this interval, will be respectively equal to 95.45% and 99.73% of the entire area under the graph (check on the STATISTICA probabilistic calculator!). In other words, it can be expressed as follows: 95.45% and 99.73% of all independent observations from the normal population, for example, the size of a part or the stock price, lie in the zone of 2- and 3-standard deviations from the mean. Even distribution Uniform distribution is useful when describing variables in which each value is equally probable, in other words, the values of a variable are evenly distributed in some area. Below are the density formulas and distribution functions of a uniform random variable taking values on the interval [a, b]. From these formulas it is easy to understand that the probability that a uniform random variable will take values from the set [c, d] [a, b] is equal to (d - c) / (b - a). We put a = 0, b = 1. Below is a graph of a uniform probability density centered on a segment. Numerical characteristics of the uniform law: Exponential distribution There are events that can be called rare in ordinary language. If T is the time between the onset of rare events occurring on average with an intensity X, then the value This distribution has a very interesting property of the absence of aftereffect, or, as they say, the Markov property, in honor of the famous Russian mathematician A.A. Markov, which can be explained as follows. If the distribution between the moments of occurrence of some events is indicative, then the distribution counted from any moment t until the next event also has an exponential distribution (with the same parameter). In other words, for a stream of rare events, the waiting time for the next visitor is always exponentially distributed, regardless of how long you have already been waiting for him. The exponential distribution is associated with the Poisson distribution: in a unit time interval, the number of events, the intervals between which are independent and exponentially distributed, has a Poisson distribution. If the intervals between site visits have an exponential distribution, then the number of visits, for example, within an hour, is distributed according to Poisson's law. The exponential distribution is a special case of the Weibull distribution. If time is not continuous, but discrete, then the analogue of the exponential distribution is the geometric distribution. The exponential distribution density is described by the formula: This distribution has only one parameter, which determines its characteristics. The exponential distribution density graph has the form: Basic numerical characteristics of exponential distribution: Erlang distribution This continuous distribution is centered on (0,1) and has a density: The mathematical expectation and variance are equal respectively The Erlang distribution is named after A. Erlang, who first applied it to problems in the theory of queuing and telephony. The Erlang distribution with parameters µ and n is the distribution of the sum of n independent, identically distributed random variables, each of which has an exponential distribution with the parameter nµ At The n = 1 Erlang distribution is the same as the exponential or exponential distribution. Laplace distribution The density function of the Laplace distribution, or, as it is also called, double exponential, is used, for example, to describe the distribution of errors in regression models. Looking at the graph of this distribution, you will see that it consists of two exponential distributions, symmetric about the OY axis. If the position parameter is 0, then the Laplace distribution density function has the form: The main numerical characteristics of this distribution law, assuming that the position parameter is zero, are as follows: In the general case, the Laplace distribution density has the form: a is the mean of the distribution; b is the scale parameter; e is Euler's number (2.71 ...). Gamma distribution The exponential distribution density has a mode at the point 0, and this is sometimes inconvenient for practical applications. In many examples, it is known in advance that the mode of the considered random variable is not equal to 0, for example, the intervals between shoppers arriving at an e-commerce store or visiting a site have a pronounced mode. The gamma distribution is used to simulate such events. The density of the gamma distribution is as follows: where Γ is Euler's Γ-function, a> 0 is the "shape" parameter and b> 0 is the scale parameter. In a particular case, we have an Erlang distribution and an exponential distribution. The main characteristics of the gamma distribution: Below are two plots of gamma density with a scale parameter of 1 and shape parameters of 3 and 5. A useful property of the gamma distribution: the sum of any number of independent gamma-distributed random variables (with the same scale parameter b) (a l, b) + (a 2, b) + --- + (a n, b) also obeys the gamma distribution, but with the parameters a 1 + a 2 + + a n and b. Lognormal distribution A random variable h is called log-normal, or log-normal, if its natural logarithm (lnh) obeys the normal distribution law. The lognormal distribution is used, for example, when modeling variables such as income, the age of newlyweds, or the tolerance from the standard for harmful substances in food. So, if the quantity x has a normal distribution, then the quantity y = e x has a Lognormal distribution. If you substitute the normal value into the exponential power, then you will easily understand that the lognormal value is obtained as a result of multiple multiplications of independent values, just as a normal random variable is the result of multiple summation. The density of the lognormal distribution is: The main characteristics of a lognormal distribution are: Chi-squared distribution The sum of squares of m independent normal values with mean 0 and variance 1 has a chi-square distribution with m degrees of freedom. This distribution is most commonly used in data analysis. Formally, the density of the well-square distribution with m degrees of freedom has the form: With negative x density turns to 0. Basic numerical characteristics of the chi-squared distribution: The density plot is shown in the figure below: Binomial distribution The binomial distribution is the most important discrete distribution that is concentrated in just a few points. The binomial distribution assigns positive probabilities to these points. Thus, the binomial distribution differs from continuous distributions (normal, chi-square, etc.), which assign zero probabilities to separately selected points and are called continuous. You can better understand the binomial distribution by looking at the following game. Imagine you are tossing a coin. Let the probability of falling out of the coat of arms be p, and the probability of getting tails is q = 1 - p (we consider the most general case when the coin is asymmetrical, has, for example, a shifted center of gravity - a hole is made in the coin). Falling the coat of arms is considered a success, and falling tails is considered a failure. Then the number of coats of arms (or tails) dropped has a binomial distribution. Note that the consideration of asymmetrical coins or irregular dice is of practical interest. As J. Neumann noted in his elegant book "An Introductory Course in Probability Theory and Mathematical Statistics," people have long guessed that the frequency of points falling on a dice depends on the properties of this dice itself and can be artificially changed. Archaeologists found two pairs of bones in the tomb of the pharaoh: "honest" - with equal probabilities of all sides falling out, and fake - with a deliberate shift of the center of gravity, which increased the probability of sixes falling out. The parameters of the binomial distribution are the probability of success p (q = 1 - p) and the number of tests n. The binomial distribution is useful for describing the distribution of binomial events, such as the number of males and females in randomly selected companies. The use of the binomial distribution in game problems is of particular importance. The exact formula for the probability t of successes in n tests are written as follows: p-probability of success q equals 1-p, q> = 0, p + q == 1 n- number of tests, m = 0.1 ... m The main characteristics of the binomial distribution: The graph of this distribution for a different number of trials n and probabilities of success p has the form: The binomial distribution is related to the normal distribution and the Poisson distribution (see below); at certain values of the parameters with a large number of tests, it turns into these distributions. This is easily demonstrated with STATISTICA. For example, considering the graph of the binomial distribution with parameters p = 0.7, n = 100 (see figure), we used STATISTICA BASIC - you can notice that the graph is very similar to the density of the normal distribution (it really is!). Binomial distribution plot with parameters p = 0.05, n = 100 is very similar to the graph of the Poisson distribution. As already mentioned, the binomial distribution arose from observations of the simplest gambling game - tossing the correct coin. In many situations, this model serves as a good first approximation for more complex games and random processes that arise when playing on the stock exchange. It is remarkable that the essential features of many complex processes can be understood from a simple binomial model. For example, consider the following situation. Let's mark the falling of the coat of arms as 1, and the falling of tails - minus 1, and we will summarize the gains and losses at successive moments of time. The graphs show the typical trajectories of such a game with 1,000 tosses, 5,000 tosses, and 10,000 tosses. Pay attention to how long the trajectory is above or below zero, in other words, the time during which one of the players is winning in an absolutely fair game is very long, and the transitions from win to loss are relatively rare, and this is difficult to fit. in an unprepared mind, for whom the expression "absolutely fair game" sounds like a magic spell. So, although the game is fair under the conditions, the behavior of a typical trajectory is not fair at all and does not show equilibrium! Of course, empirically this fact is known to all players, a strategy is associated with it, when the player is not allowed to leave with a win, but is forced to play further. Consider the number of throws during which one player wins (trajectory above 0), and the other loses (trajectory below 0). At first glance, it seems that the number of such throws is about the same. However (see the fascinating book: Feller V. "Introduction to the theory of probability and its applications." Moscow: Mir, 1984, p. 106) with 10,000 tosses of an ideal coin p = q = 0.5, n = 10,000) the probability that one of the parties will lead for more than 9,930 trials, and the other - less than 70, exceeds 0.1. Surprisingly, in a game of 10,000 tosses of the correct coin, the probability of a leadership change no more than 8 times is greater than 0.14, and the probability of more than 78 leadership changes is approximately 0.12. So, we have a paradoxical situation: in Bernoulli's symmetric walk, the “waves” on the chart between successive zero returns (see charts) can be surprisingly long. This is connected with another circumstance, namely that for T n / n (the fraction of time when the graph is above the abscissa axis) the least probable values are close to 1/2. Mathematicians discovered the so-called arcsine law, according to which for each 0< а <1 вероятность неравенства
, где Т n - число шагов, в течение которых первый игрок находится в выигрыше, стремится к Arcsine distribution This continuous distribution is concentrated on the interval (0, 1) and has a density: The inverse sine distribution is associated with a random walk. This is the distribution of the proportion of time during which the first player is winning when throwing a symmetrical coin, that is, a coin that with equal probabilities S falls on coat of arms and tails. In another way, such a game can be viewed as a random walk of a particle that, starting from zero, makes unit jumps to the right or to the left with equal probabilities. Since the jumps of the particle - the appearance of the coat of arms or tails - are equally probable, such a walk is often called symmetric. If the probabilities were different, then we would have an asymmetric walk. The graph of the distribution density of the arcsine is shown in the following figure: The most interesting thing is the high-quality interpretation of the chart, from which you can draw amazing conclusions about the winning streak and losing streak in a fair game. Looking at the graph, you can see that the density minimum is at the point 1/2. "So what ?!" - you ask. But if you think about this observation, then there will be no bounds to your surprise! It turns out that when defined as fair, the game is actually not as fair as it might seem at first glance. Trajectories of a symmetric random, in which a particle spends equal time on both the positive and negative semiaxes, that is, to the right or to the left of zero, are just the least probable. Moving on to the language of the players, we can say that when throwing a symmetrical coin, games in which the players are equal time winning and losing are the least likely. On the contrary, games in which one player is significantly more likely to win, and the other, respectively, to lose, are the most likely. An amazing paradox! To calculate the probability that the fraction of time t during which the first player wins lies in the range from t1 to t2, it is necessary from the value of the distribution function F (t2) subtract the value of the distribution function F (t1). Formally we get: P (t1 Based on this fact, it is possible to calculate using STATISTICA that at 10,000 steps the particle remains on the positive side of more than 9930 time instants with a probability of 0.1, that is, roughly speaking, such a situation will be observed at least in one case out of ten. (although, at first glance, it seems absurd; see the remarkably clear note by Yu. V. Prokhorov "Bernoulli's Walk" in the encyclopedia "Probability and Mathematical Statistics", pp. 42-43, Moscow: Big Russian Encyclopedia, 1999) ... Negative binomial distribution This is a discrete distribution that assigns to the whole points k = 0,1,2, ... probabilities: p k = P (X = k) = C k r + k-1 p r (l-p) k ", where 0<р<1,r>0.
The negative binomial distribution is found in many applications. In general r> 0 negative binomial distribution is interpreted as the distribution of the waiting time for the rth "success" in the Bernoulli test scheme with the probability of "success" p, for example, the number of rolls to be made before the second coat of arms is rolled, in which case it is sometimes called the Pascal distribution and is a discrete analogue of the gamma distribution. At r = 1 negative binomial distribution coincides with geometric distribution. If Y is a random variable with a Poisson distribution with a random parameter, which, in turn, has a gamma distribution with density Then Ub will have a negative binomial distribution with parameters; Poisson distribution The Poisson distribution is sometimes referred to as the rare event distribution. Examples of variables distributed according to Poisson's law are: the number of accidents, the number of defects in the manufacturing process, etc. The Poisson distribution is determined by the formula: The main characteristics of a Poisson random variable: The Poisson distribution is related to the exponential distribution and the Bernoulli distribution. If the number of events has a Poisson distribution, then the intervals between events have an exponential or exponential distribution. Poisson Distribution Plot: Compare the plot of the Poisson distribution with parameter 5 with the plot of the Bernoulli distribution at p = q = 0.5, n = 100. You will see that the graphs are very similar. In the general case, there is the following pattern (see, for example, the excellent book: Shiryaev A. N. “Probability.” Moscow: Nauka, p. 76): if in Bernoulli's tests n takes large values, and the probability of success /? is relatively small, so that the average number of successes (product and bp) is neither small nor large, then the Bernoulli distribution with parameters n, p can be replaced by the Poisson distribution with parameter = np. Poisson's distribution is widely used in practice, for example, in quality control charts as a distribution of rare events. As another example, consider the following problem related to telephone lines and taken from practice (see: Feller V. Introduction to the theory of probability and its applications. Moscow: Mir, 1984, p. 205, and also Molina E. S. (1935 ) Probability in engineering, Electrical engineering, 54, p. 423-427; Bell Telephone System Technical Publications Monograph B-854). This task is easy to translate into a modern language, for example, into the language of mobile communications, which is what interested readers are invited to do. The problem is formulated as follows. Let there be two telephone exchanges - A and B. Telephone station A must ensure communication of 2,000 subscribers with station B. The quality of communication must be such that only 1 call out of 100 waits for the line to become free. The question is: how many telephone lines do you need to lay in order to ensure the given quality of communication? Obviously, it is foolish to create 2,000 lines, since many of them will be free for a long time. From intuitive considerations it is clear that, apparently, there is some optimal number of lines N. How to calculate this number? Let's start with a realistic model that describes the intensity of the subscriber's access to the network, while note that the accuracy of the model can, of course, be checked using standard statistical criteria. So, suppose that each subscriber uses the line on average 2 minutes per hour and the subscriber connections are independent (however, as Feller rightly notes, the latter takes place if there are no events that affect all subscribers, for example, a war or a hurricane). We then have 2000 Bernoulli trials (coin tosses) or network connections with a success rate of p = 2/60 = 1/30. You need to find such N when the probability that more than N users are simultaneously connected to the network does not exceed 0.01. These calculations can be easily solved in the STATISTICA system. Solving the problem on STATISTICA. Step 1. Open the module Basic statistics... Create a binoml.sta file containing 110 observations. Name the first variable BINOMIAL, the second variable is POISSON. Step 2. BINOMIAL, Open the window Variable 1(see fig.). Enter the formula in the window as shown in the figure. Click the button OK. Step 3. By double clicking on the title POISSON, Open the window Variable 2(see fig.) Enter the formula in the window as shown in the figure. Note that we are calculating the parameter of the Poisson distribution using the formula = n × p. Therefore = 2000 × 1/30. Click the button OK.
STATISTICA will calculate the probabilities and write them to the generated file. Step 4. Scroll through the constructed table to cases numbered 86. You will see that the probability that 86 or more out of 2000 network users work simultaneously for an hour is 0.01347 if the binomial distribution is used. The probability that 86 or more people out of 2,000 network users work concurrently for an hour is 0.01293 when using the Poisson approximation for the binomial distribution. Since we need a probability of no more than 0.01, then 87 lines will be enough to provide the required communication quality. Similar results can be obtained by using the normal approximation for the binomial distribution (check it out!). Note that V. Feller did not have the STATISTICA system at his disposal and used tables for the binomial and normal distribution. Using the same reasoning, one can solve the following problem discussed by W. Feller. It is required to check whether more or less lines will be required to reliably service users when dividing them into 2 groups of 1000 people each. It turns out that dividing users into groups will require an additional 10 lines to achieve the same quality level. You can also take into account the change in the intensity of the network connection during the day. Geometric distribution If independent Bernoulli tests are carried out and the number of tests is counted until the next "success" occurs, then this number has a geometric distribution. Thus, if you flip a coin, then the number of tosses that you need to do before the next coat of arms falls out obeys a geometric law. The geometric distribution is determined by the formula: F (x) = p (1-p) x-1 p is the probability of success, x = 1, 2,3 ... The distribution name is associated with a geometric progression. So, the geometric distribution sets the probability that success came at a certain step. The geometric distribution is a discrete analogue of the exponential distribution. If time changes in quanta, then the probability of success at each moment of time is described by a geometric law. If time is continuous, then the probability is described by an exponential or exponential law. Hypergeometric distribution This is a discrete probability distribution of a random variable X taking integer values m = 0, 1,2, ..., n with probabilities: where N, M and n are non-negative integers and M<
N, n < N. The hypergeometric distribution is usually associated with a choice without recurrence and determines, for example, the probability of finding exactly m black balls in a random sample of size n from a general population containing N balls, including M black and N - M white (see, for example, the encyclopedia “Probability and mathematical statistics ”, Moscow: Great Russian Encyclopedia, p. 144). The mathematical expectation of the hypergeometric distribution does not depend on N and coincides with the mathematical expectation µ = np of the corresponding binomial distribution. Dispersion of the hypergeometric distribution This distribution is extremely common in quality control tasks. Polynomial distribution A polynomial, or multinomial, distribution naturally generalizes the distribution. If the binomial distribution occurs when a coin is tossed with two outcomes (lattice or coat of arms), then the polynomial distribution occurs when a die is rolled and there are more than two possible outcomes. Formally, this is the joint probability distribution of random variables X 1, ..., X k, taking integer non-negative values n 1, ..., n k, satisfying the condition n 1 + ... + n k = n, with probabilities: The name "polynomial distribution" is explained by the fact that multinomial probabilities arise during the expansion of the polynomial (p 1 + ... + p k) n Beta distribution The beta distribution has a density of the form: The standard beta distribution is concentrated in the range from 0 to 1. Applying linear transformations, the beta value can be transformed so that it will take values at any range. The main numerical characteristics of a quantity with a beta distribution: Distribution of extreme values The distribution of extreme values (type I) has a density of the form: This distribution is sometimes also referred to as the extreme distribution. The extreme value distribution is used to model extreme events, such as flood levels, vortex velocities, the maximum of stock market indices for a given year, etc. This distribution is used in reliability theory, for example, to describe the failure time of electrical circuits, as well as in actuarial calculations. Rayleigh distribution The Rayleigh distribution has a density of the form: where b is the scale parameter. The Rayleigh distribution is concentrated in the range from 0 to infinity. Instead of 0, STATISTICA allows you to enter another value for the threshold parameter, which will be subtracted from the original data before fitting the Rayleigh distribution. Therefore, the value of the threshold parameter should be less than all observed values. If two variables y 1 and y 2 are independent of each other and are normally distributed with the same variance, then the variable The Rayleigh distribution is used, for example, in shooting theory. Weibull distribution The Weibull distribution is named after the Swedish researcher Waloddi Weibull, who used this distribution to describe different types of failure times in reliability theory. Formally, the Weibull distribution density is written in the form: Sometimes the Weibull distribution density is also written in the form: B is the scale parameter; С - shape parameter; E is Euler's constant (2.718 ...). Position parameter. Typically, the Weibull distribution is centered on the semiaxis from 0 to infinity. If, instead of the boundary 0, we introduce the parameter a, which is often necessary in practice, then the so-called three-parameter Weibull distribution arises. The Weibull distribution is used extensively in the theory of reliability and insurance. As described above, exponential distribution is often used as a model for estimating MTBF under the assumption that the probability of a facility's failure is constant. If the probability of failure changes over time, the Weibull distribution is applied. At c = 1 or, in another parameterization, at, the Weibull distribution, as is easy to see from the formulas, transforms into an exponential distribution, and at, into the Rayleigh distribution. Special methods have been developed for estimating the parameters of the Weibull distribution (see, for example, the book: Lawless (1982) Statistical models and methods for lifetime data, Belmont, CA: Lifetime Learning, which describes the estimation methods, as well as the problems that arise when estimating the position parameter for a three-parameter distribution Weibull). Often, when performing a reliability analysis, it is necessary to consider the probability of failure within a short time interval after a point in time. t provided that until the moment t no failure occurred. Such a function is called the risk function, or the failure rate function, and is formally defined as follows: H (t) - function of failure rate or risk function at time t; f (t) - distribution density of failure times; F (t) - distribution function of failure times (integral of density over the interval). In general terms, the failure rate function is written as follows: When the risk function is equal to a constant, which corresponds to the normal operation of the device (see formulas). At, the risk function decreases, which corresponds to the running-in of the device. At, the risk function decreases, which corresponds to the aging of the device. Typical risk functions are shown in the graph. Weibull density plots with different parameters are shown below. It is necessary to pay attention to three ranges of values of the parameter a: In the first area, the risk function decreases (tuning period), in the second area, the risk function is equal to a constant, in the third area, the risk function increases. You can easily understand what has been said for the example of buying a new car: first there is a period of adaptation of the car, then a long period of normal operation, then the car parts wear out and the risk of its failure increases sharply. It is important that all periods of operation can be described by the same distribution family. This is the idea of the Weibull distribution. Here are the main numerical characteristics of the Weibull distribution. Pareto distribution In various problems of applied statistics, so-called truncated distributions are often encountered. For example, this distribution is used in insurance or in taxation when incomes are of interest that exceed a certain value c 0 The main numerical characteristics of the Pareto distribution: Logistic distribution The logistic distribution has a density function: A - position parameter; B is the scale parameter; E is Euler's number (2.71 ...). Hotelling T 2 -distribution This continuous distribution, concentrated on the interval (0, T), has a density: where the parameters n and k, n> _k> _1, are called degrees of freedom. At Hotelling's k = 1, the P-distribution reduces to the Student's distribution, and for any k> 1 can be considered as a generalization of the Student distribution to the multidimensional case. The Hotelling distribution is based on the normal distribution. Let a k-dimensional random vector Y have a normal distribution with zero mean vector and covariance matrix. Consider the value where random vectors Z i are independent of each other and Y and are distributed in the same way as Y. Then the random variable T 2 = Y T S -1 Y has the T 2-Hotelling distribution with n degrees of freedom (Y is a column vector, T is the transposition operator). where the random variable t n has a Student's distribution with n degrees of freedom (see "Probability and Mathematical Statistics", Encyclopedia, p. 792). If Y has a normal distribution with a nonzero mean, then the corresponding distribution is called off-center Hotelling T 2 -distribution with n degrees of freedom and noncentrality parameter v. Hotelling's T 2 -distribution is used in mathematical statistics in the same situation as the Student's t-distribution, but only in the multidimensional case. If the results of observations X 1, ..., X n are independent, normally distributed random vectors with a mean vector µ and a non-degenerate covariance matrix, then the statistics has a Hotelling T 2 -distribution with n - 1 degrees of freedom. This fact forms the basis of Hotelling's criterion. In STATISTICA, the Hotelling criterion is available, for example, in the Basic Statistics and Tables module (see the dialog box below). Maxwell distribution The Maxwell distribution arose in physics when describing the distribution of the velocities of ideal gas molecules. This continuous distribution is centered on (0,) and has a density: The distribution function has the form: where Ф (x) is the standard normal distribution function. The Maxwell distribution has a positive skewness coefficient and a single mode at a point (that is, the distribution is unimodal). The Maxwell distribution has finite moments of any order; the mathematical expectation and variance are equal, respectively, and The Maxwell distribution is naturally related to the normal distribution. If X 1, X 2, X 3 are independent random variables with normal distribution with parameters 0 and х 2, then the random variable Cauchy distribution This amazing distribution sometimes does not have an average value, since its density very slowly tends to zero with increasing x in absolute value. Such distributions are called heavy-tailed distributions. If you need to come up with a distribution that has no mean, then immediately call the Cauchy distribution. The Cauchy distribution is unimodal and symmetric with respect to the mode, which is simultaneously the median and has a density function of the form: where c> 0 is the scale parameter and a is the center parameter, which simultaneously determines the values of the mode and median. The integral of the density, that is, the distribution function is given by: Student's t distribution The English statistician V. Gosset, known under the pseudonym "Student" and who began his career with a statistical study of the quality of English beer, received in 1908 the following result. Let be x 0, x 1, .., x m - independent, (0, s 2) - normally distributed random variables: This distribution, now known as the Student's t distribution (abbreviated as t (m) -distributions, where m is the number of degrees of freedom), underlies the famous t-test designed to compare the means of two populations. Density function f t (x) does not depend on the variance х 2 of random variables and, moreover, is unimodal and symmetric with respect to the point х = 0. Basic numerical characteristics of the Student's distribution: The t-distribution is important when estimates of the mean are considered and the sample variance is unknown. In this case, the sample variance and t-distribution are used. At large degrees of freedom (greater than 30), the t-distribution practically coincides with the standard normal distribution. The graph of the density function of the t-distribution deforms with increasing number of degrees of freedom as follows: the peak increases, the tails go more steeply to 0, and it seems as if the graphs of the density function of the t-distribution are compressed laterally. F-distribution Consider m 1 + m 2 independent and (0, s 2) normally distributed quantities Obviously, the same random variable can be defined as the ratio of two independent and appropriately normalized chi-square-distributed quantities and, that is The famous English statistician R. Fisher in 1924 showed that the probability density of a random variable F (m 1, m 2) is given by the function: where Γ (y) is the value of Euler's gamma function in. point y, and the law itself is called the F-distribution with the numbers of degrees of freedom of the numerator and denominator equal to m, 1 and m7, respectively Basic numerical characteristics of the F-distribution: The F-distribution occurs in discriminant, regression and analysis of variance, and other types of multivariate data analysis.
T has an exponential distribution with a parameter (lambda). Exponential distribution is often used to describe the interval between successive random events, such as the interval between visits to an unpopular site, since these visits are rare events.
does not exceed the variance of the binomial distribution npq. For moments of any order, the hypergeometric distribution tends to the corresponding values of the moments of the binomial distribution.
will have a Rayleigh distribution.
has a Maxwell distribution. Thus, the Maxwell distribution can be considered as the distribution of the length of a random vector, the coordinates of which in the Cartesian coordinate system in three-dimensional space are independent and normally distributed with mean 0 and variance x 2.
and put
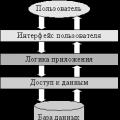Architecture of a distributed control system based on a reconfigurable multi-pipeline computing environment L-Net "transparent" distributed file systems
Email sending page Fill relay_recipients file with addresses from Active Directory
Missing language bar in Windows - what to do?