Laplace transforms examples. Laplace transform. To solve linear differential equations, we will use the Laplace transform. Examples of calculating Laplace transforms
To solve linear differential equations, we will use the Laplace transform.
Laplace transform call the ratio
assigning functions x (t) real variable t match function X (s) complex variable s (s = σ+ jω). Wherein x (t) are called original, X (s)- image or Laplace image and s- Laplace transform variable. The original is denoted in lowercase, and its image is in the capitalized letter of the same name.
It is assumed that the function x(t) subject to the Laplace transform has the following properties:
1) function x (t) is defined and piecewise differentiable on an interval. The exact infimum s0 of all numbers s, α0 = infs, for which inequality (1) holds, is called the growth rate of the function f (t). Comment. In the general case, the inequality does not hold, but the estimate is valid where e> 0 is any. So, the function has an exponent of growth в0 = For it, the inequality \ t \ ^ M V * ^ 0 does not hold, but the inequality | f | ^ Mei. Condition (1) is much less restrictive than condition (*). Example 1. the function does not satisfy condition ("), but condition (1) is satisfied for any s> I and A /> I; growth rate 5o = So this is the original function. On the other hand, the function is not an original function: it has an infinite order of growth, “o = + oo. The simplest original function is the so-called unit function. If some function satisfies conditions 1 and 3 of Definition 1, but does not satisfy condition 2, then the product is already an original function. For simplicity of notation, we will, as a rule, omit the factor rj (t), having agreed that all functions that we will consider are equal to zero for negative t, so that if we are talking about some function f (t), for example, o sin ty cos t, el, etc., then the following functions are always implied (Fig. 2): n = n (0 Fig. 1 Definition 2. Let f (t) be the original function. The image of the function f (t ) by Laplace is the function F (p) of a complex variable defined by the formula LAPLACE TRANSFORM Basic definitions Properties Convolution of functions Multiplication theorem Finding the original from the image Using the inversion theorem for operational calculus Duhamel's formula Integration of systems of linear differential equations with constant coefficients Solution of integral equations where the integral is taken over the positive of the semiaxis t. The function F (p) is also called the Laplace transform of the function f (f); the kernel of the transformation K (t) p) = e ~ pt. The fact that the function has its image F (p), we will write Example 2. Find the image unit function r) (t). The function is an original function with a growth rate of 0 - 0. By virtue of formula (2), the image of the function rj (t) will be the function If then for, the integral on the right-hand side of the last equality will converge, and we get so that the image of the function rj (t) will be function £. As we agreed, we will write that rj (t) = 1, and then the result obtained will be written as follows: Theorem 1. For any original function f (t) with growth exponent z0, the image F (p) is defined in the half-plane R ep = s > s0 and is an analytic function in this half-plane (Fig. 3). Let To prove the existence of the image F (p) in the indicated half-plane, it suffices to establish that the improper integral (2) converges absolutely for a> Using (3), we obtain which proves the absolute convergence of the integral (2). At the same time, we obtained an estimate for the Laplace transform F (p) in the half-plane of convergence Differentiating expression (2) formally under the integral sign with respect to p, we find that the existence of integral (5) is established in the same way as the existence of integral (2) was established. Applying integration by parts for F "(p), we obtain an estimate which implies the absolute convergence of the integral (5). (The non-integral term, 0., - for t + oo has a limit equal to zero). integral (5) converges uniformly with respect to p, since it is majorized by a convergent integral independent of p. Consequently, differentiation with respect to p is legal and equality (5) is valid. Since the derivative F "(p) exists, the Laplace transform F (p) everywhere in the half-plane Rep = 5> 5о is an analytical function. Inequality (4) implies Corollary. If thin p tends to infinity so that Re p = s increases indefinitely, then Example 3. Let us also find the image of the function any complex number. The exponent of the function f (() is equal to a. > a, but also at all points p, except for the point p = a, where this image has a simple pole. In the future, we will repeatedly encounter a similar situation when the image F (p) is an analytic function in the entire plane of the complex variable p, for there is no contradiction with Theorem 1. The latter asserts only that in the half-plane Rep> «o the function F (p) has no singular points: they all turn out to lie either to the left of the line Rep = so, or on this line itself. Notice not. In operational calculus, the Heaviside image of the function f (f) is sometimes used, which is defined by equality and differs from the Laplace image by the factor p. §2. Properties of the Laplace transform In what follows, we will denote the original functions, and through - their images according to Laplace. £ biw dee are continuous functions) have the same image, then they are identically equal. Teopewa 3 (n "yeyiost * transforming Laplace). If the functions are original, then for any complex constants of the air The validity of the statement follows from the linearity property of the integral that determines the image:, are the growth rates of functions, respectively). Based on this property, we obtain Similarly, we find that and, further, Theorem 4 (similarities). If f (t) is the original function and F (p) is its Laplace image, then for any constant a> 0 Putting at = m, we have Using this theorem, from formulas (5) and (6) we obtain Theorem 5 ( on the differentiation of the original). Let be the original function with the image F (p) and let - also be the original functions, and where is the growth rate of the function Then and in general Here we mean the right limiting value Let. Let us find the image We have Integrating by parts, we obtain The non-integral term on the right-hand side of (10) vanishes at k. For Rc p = s> h we have the substitution t = Odet - / (0). The second term on the right in (10) is equal to pF (p). Thus, relation (10) takes the form and formula (8) is proved. In particular, if To find the image f (n \ t) we write whence, integrating n times by parts, we get Example 4. Using the theorem on the differentiation of the original, find the image of the function f (t) = sin2 t. Let Consequently, Theorem 5 establishes a remarkable property of the Laplace integral transform: it (like the Fourier transform) transforms the operation of differentiation into an algebraic operation of multiplication by p. Inclusion formula. If they are original functions, then Indeed, By virtue of the corollary to Theorem 1, any image tends to zero as. Hence, whence the inclusion formula follows (Theorem 6 (on the differentiation of the image). Differentiation of the image is reduced to multiplication by the original, Since the function F (p) in the half-plane so is analytic, it can be differentiated with respect to p. Example 5. Using Theorem 6, find the image of the function 4 As is known, Hence (Using Theorem 6 again, we find, in general, Theorem 7 (integration of the original). Integration of the original is reduced to dividing the image by Let It is easy to check that if there is an original function, then it will be an original function, moreover. Let be. By virtue of so that On the other hand, whence F = The latter is equivalent to the proved relation (13). Example 6. Find the image of the function M In this case, so. Therefore, Theorem 8 (image integration). If the integral also converges, then it serves as an image of the function ^: LAPLACE TRANSFORM Basic definitions Properties Convolution of functions Multiplication theorem Finding the original from the image Using the inverse theorem of operational calculus Duhamel's formula Integration of systems of linear differential equations with constant coefficients Solution of integral equations Indeed, Assuming that the path of integration lie on the half-plane so, we can change the order of integration. The last equality means that it is an image of a function Example 7. Find an image of a function M As is known,. Therefore, Since we put, we obtain £ = 0, for. Therefore, relation (16) takes the form Example. Find an image of the function f (t) given graphically (Fig. 5). Let's write the expression for the function f (t) as follows: This expression can be obtained as follows. Consider the function and subtract the function from it The difference will be equal to one for. We add the function to the resulting difference. As a result, we obtain the function f (t) (Fig. 6 c), so that From here, using the delay theorem, we find Theorem 10 (displacement). then for any complex number po In fact, the theorem allows, from known images of functions, to find images of the same functions multiplied by an exponential function, for example, 2.1. Convolution of functions. Multiplication theorem Let the functions f (t) u be defined and continuous for all t. The convolution of these functions is called new function from t, defined by equality (if this integral exists). For the original functions, the operation is always collapsible, and (17) 4 Indeed, the product of the original functions as a function of m is a finite function, i.e. vanishes outside some finite interval (in this case, outside the interval. For finite continuous functions, the convolution operation is satisfiable, and we obtain the formula It is easy to verify that the convolution operation is commutative, Theorem 11 (multiplication). If, then the convolution t) has an image that the convolution (of the original functions is the original function with the growth exponent "where, are the growth exponents of the functions, respectively. Let us find the image of the convolution, Using what we have Changing the order of integration in the integral on the right (such an operation is legal) and applying the delay theorem, we obtain Thus, from (18) and (19) we find that the multiplication of images corresponds to the convolution of the originals, Prter 9. Find the image of a function A function V (0 is a convolution of functions. By virtue of the multiplication theorem Problem. Let the function f (t) be periodic with period T , ecg is the original function Show that its Laplace image F (p) is given by formula 3. Finding the original from the image The problem is posed as follows: For the function F (p), we need to find the function / (<)>whose image is F (p). Let us formulate conditions sufficient for the function F (p) of a complex variable p to serve as an image. Theorem 12. If a function F (p) 1) analytic in the half-plane so tends to zero for in any half-plane R s0 uniformly with respect to arg p; 2) the integral converges absolutely, then F (p) is an image of some original function Problem. Can the function F (p) = serve as an image of some original function? We will indicate some of the ways to find the original from the image. 3.1. Finding the original using image tables First of all, it is worth bringing the function F (p) to a simpler, "tabular" form. For example, in the case when F (p) is a fractional rational function of the argument p, it is decomposed into elementary fractions and the appropriate properties of the Laplace transform are used. Example 1. Find the original for Let us write the function F (p) in the form Using the displacement theorem and the linearity property of the Laplace transform, we obtain Example 2. Find the original for the function 4 Let us write F (p) as Hence 3.2. Use of the inversion theorem and its consequences. Theorem 13 (inversion). If the function fit) is an original function with growth exponent s0 and F (p) is its image, then at any point of continuity of the function f (t), the relation holds where the integral is taken along any straight line and is understood in the sense of the principal value, i.e. as Formula (1) is called the Laplace transform inversion formula, or Mellin's formula. Indeed, let, for example, f (t) be piecewise smooth on every finite segment, where< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
8 Lecture 7 OPERATOR FUNCTIONS OF CIRCUITS Operator input and transfer functions Poles and zeros of circuit functions 3 Conclusions Operator input and transfer functions An operator function of a chain is a relation
68 Lecture 7 TRANSITION PROCESSES IN FIRST ORDER CIRCUITS Plan 1 Transient processes in RC-circuits of the first order 2 Transient processes in R-circuits of the first order 3 Examples of calculation of transient processes in circuits
4 LINEAR ELECTRIC CIRCUITS OF AC SINUSOIDAL CURRENT AND METHODS OF THEIR CALCULATION 4.1 ELECTRIC MACHINES. SINUSOIDAL CURRENT GENERATION PRINCIPLE 4.1.012. Sinusoidal current is called instantaneous
Federal Agency for Education State Educational Institution of Higher Professional Education "KUBAN STATE UNIVERSITY" Faculty of Physics and Technology Department of Optoelectronics
~ ~ FKP Derivative of the function of a complex variable FKP of the Cauchy - Riemann condition the concept of regularity of the FKP Image and form of a complex number Form of the FKP: where the real function of two variables is real
 Wireless Charging Smartphones A5 Supports Wireless Charging
Wireless Charging Smartphones A5 Supports Wireless Charging Why do not MTS sms come to the phone?
Why do not MTS sms come to the phone?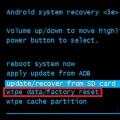 Why do you need a full factory reset on Android or how to return Android to factory settings
Why do you need a full factory reset on Android or how to return Android to factory settings