صورة من تحويل لابلاس الأصلي. تعريفات خاصية تحويل لابلاس الأساسية هي صيغة دوهاميل. تحويل لابلاس المباشر
لحل الخطي المعادلات التفاضليةسنستخدم تحويل لابلاس.
تحويل لابلاساستدعاء النسبة
إسناد الوظائف س (ر)متغير حقيقي روظيفة المباراة X (ق)متغير معقد ق (ق = σ+ ي).حيث س (ر)وتسمى أصلي ، X (ق)- صورةأو صورة لابلاسو س- متغير تحويل لابلاس.يُرمز إلى الأصل بأحرف صغيرة ، وصورته مكتوبة بالحرف الكبير الذي يحمل نفس الاسم.
من المفترض أن الوظيفة x(ر) تخضع لتحويل لابلاس الخصائص التالية:
1) الوظيفة س (ر)يتم تعريفه وقابل للتفاضل متعدد التعريف على الفاصل الزمني حيث< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
8 المحاضرة 7 وظائف مشغل الدوائر وظائف إدخال وتحويل المشغل أعمدة وأصفار وظائف الدائرة 3 الاستنتاجات وظائف إدخال ونقل المشغل وظيفة مشغل سلسلة هي علاقة
68 المحاضرة 7 عمليات الانتقال في دوائر الترتيب الأول الخطة 1 عمليات عابرة في دوائر RC من الدرجة الأولى 2 عمليات عابرة في دوائر R من الدرجة الأولى 3 أمثلة لحساب العمليات العابرة في الدوائر
4 الدوائر الكهربائية الخطية للتيار الجيني المتردد وطرق حسابها 4.1 الآلات الكهربائية. مبدأ الجيل الحالي للجيوب الأنفية 4.1.012. يسمى التيار الجيبي لحظية
الوكالة الفيدرالية للتعليم المؤسسة التعليمية الحكومية للتعليم المهني العالي "جامعة ولاية كوبان" كلية الفيزياء والتكنولوجيا قسم الإلكترونيات الضوئية
~ ~ FKP مشتق من وظيفة متغير معقد FKP لشرط Cauchy - Riemann شرط مفهوم انتظام صورة FKP وشكل رقم مركب من FKP: حيث تكون الوظيفة الحقيقية لمتغيرين حقيقيين
القسم الثاني. التحليل الرياضي
إي يو. أنوخينا
تاريخ التطور وصياغة نظرية وظيفة متغير معقد (TFKP) بواسطة موضوع تعليمي
تعتبر دورة TFKP واحدة من دورات الرياضيات الصعبة. يرجع تعقيد هذه الدورة ، أولاً وقبل كل شيء ، إلى تنوع علاقاتها المتبادلة مع التخصصات الرياضية الأخرى ، التي تم التعبير عنها تاريخيًا في الاتجاه التطبيقي الواسع لعلم TFKP.
في الأدبيات العلمية حول تاريخ الرياضيات ، توجد معلومات متفرقة حول تاريخ تطور TFKP ، فهي تتطلب تنظيمًا وتعميمًا.
في هذا الصدد ، تتمثل المهمة الرئيسية لهذه المقالة في وصف موجز لتطور TFKP وتشكيل هذه النظرية كموضوع أكاديمي.
نتيجة للدراسة ، تم تحديد المراحل الثلاث التالية في تطوير TFKP كموضوع علمي وأكاديمي:
مرحلة ظهور الأعداد المركبة والتعرف عليها ؛
مرحلة تراكم المادة الواقعية وفقًا لوظائف القيم التخيلية ؛
مرحلة تكوين نظرية وظائف المتغير المعقد.
تبدأ المرحلة الأولى في تطوير TFKP (منتصف القرن السادس عشر - القرن الثامن عشر) بعمل ج. كاردانو (1545) الذي نشر العمل "Artis magnae sive de regulis algebraitis" (الفن العظيم ، أو حول القواعد الجبرية) . كان لعمل ج. كاردانو المهمة الرئيسية لإثبات الطرق الجبرية العامة لحل المعادلات من الدرجة الثالثة والرابعة ، قبل وقت قصير من اكتشاف فيرو (1465-1526) ، تارتاليا (1506-1559) وفيراري (1522) -1565). إذا تم تقليل المعادلة التكعيبية إلى النموذج
x3 + بكسل + q = 0 ،
ويجب أن يكون هناك
عندما يكون (μ ^ Ap V (| - 70) يكون للمعادلة ثلاثة جذور حقيقية ، اثنان منهم
متساوون. إذا كانت المعادلة تحتوي على واحد حقيقي واثنان
جذر معقد ملتوي. تظهر الأرقام المعقدة في النتيجة النهائية ، لذلك كان بإمكان G.Cardano أن يفعل ما فعله قبله: أعلن أن المعادلة لديها
جذر واحد. متي (<7 Г + (р V < (). тогда уравнение имеет три действительных корня. Этот так
تتميز الحالة المسماة غير القابلة للاختزال بخصوصية واحدة لم تتم مواجهتها حتى القرن السادس عشر. المعادلة x3 - 21x + 20 = 0 لها ثلاثة جذور حقيقية 1 ، 4 ، - 5 وهو أمر سهل
تأكد من خلال الاستبدال البسيط. لكن ^ du + y _ ^ 20y + ^ -21y _ ^ ^ ^ ؛ لذلك ، وفقًا للصيغة العامة ، x = ^ -10 + ^ -243 - ^ - 10-4 ^ 243. معقدة ، أي "خطأ" ، فالعدد ليس النتيجة هنا ، ولكنه مصطلح وسيط في الحسابات يؤدي إلى الجذور الحقيقية للمعادلة المعنية. واجه J.Cardano صعوبة وأدرك أنه من أجل الحفاظ على عمومية هذه الصيغة ، من الضروري التخلي عن الجهل الكامل للأعداد المركبة. يعتقد J. D'Alembert (1717-1783) أن هذا الظرف هو الذي جعل J. Cardano وعلماء الرياضيات الذين تبعوا هذه الفكرة مهتمين بجدية بالأعداد المركبة.
في هذه المرحلة (في القرن السابع عشر) ، تم قبول وجهتي نظر بشكل عام. تم التعبير عن وجهة النظر الأولى بواسطة Girard ، الذي أثار مسألة الاعتراف بالحاجة إلى الاستخدام غير المحدود للأعداد المركبة من قبل أي شيء. والثاني هو ديكارت ، الذي نفى إمكانية تفسير الأعداد المركبة. عكس رأي ديكارت كان وجهة نظر جيه واليس - حول وجود تفسير حقيقي للأعداد المركبة تم تجاهلها من قبل ديكارت. بدأ استخدام الأعداد المعقدة في "إجبار" على استخدامها في حل المشكلات التطبيقية في المواقف التي يؤدي فيها استخدام الأعداد الحقيقية إلى نتيجة معقدة ، أو لا يمكن الحصول على النتيجة نظريًا ، ولكن كان لها تطبيق عملي.
أدى الاستخدام البديهي للأعداد المركبة إلى الحاجة إلى الحفاظ على قوانين وقواعد حساب الأعداد الحقيقية لمجموعة من الأعداد المركبة ، على وجه الخصوص ، كانت هناك محاولات لنقل المباشر. هذا أدى في بعض الأحيان إلى نتائج خاطئة. في هذا الصدد ، أصبحت الأسئلة المتعلقة بتبرير الأعداد المركبة وبناء الخوارزميات لحسابها موضوعيًا. كانت هذه بداية مرحلة جديدة في تطوير TFKP.
المرحلة الثانية في تطوير TFKP (أوائل القرن الثامن عشر - القرن التاسع عشر). في القرن الثامن عشر. أعرب L. Euler عن فكرة التقارب الجبري لمجال الأعداد المركبة. أدى الانغلاق الجبري لمجال الأعداد المركبة C علماء الرياضيات إلى الاستنتاجات التالية:
أن تكتسب دراسة الوظائف والتحليل الرياضي بشكل عام الاكتمال والاكتمال المناسبين فقط عند النظر في سلوك الوظائف في مجال معقد ؛
من الضروري اعتبار الأعداد المركبة كمتغيرات.
في عام 1748 ، قدم ل. أويلر (1707-1783) في عمله "مقدمة في تحليل متناهيات الصغر" متغيرًا معقدًا باعتباره المفهوم الأكثر عمومية للمتغير ، باستخدام الأعداد المركبة في توسيع الوظائف إلى عوامل خطية. يعتبر L. Euler بحق أحد مؤسسي TFKP. في أعمال L.Euler ، تمت دراسة الدوال الأولية لمتغير معقد (1740-1749) بالتفصيل ، وأعطيت شروط التفاضل (1755) وبداية حساب التفاضل والتكامل لدوال متغير معقد (1777). قدم ل. أويلر رسم الخرائط المطابقة عمليًا (1777). ووصف هذه التعيينات بأنها "متشابهة في صغيرة" ، ومصطلح "امتثال" استخدم لأول مرة ، على ما يبدو ، من قبل الأكاديمي في سانت بطرسبرغ ف. شوبرت (1789). قاد ل. أويلر أيضًا تطبيقات عديدة لوظائف متغير معقد لمشاكل رياضية مختلفة ووضع الأساس لتطبيقها في الديناميكا المائية (1755-1757) ورسم الخرائط (1777). يصوغ K. Gauss تعريف التكامل في المستوى المركب ، وهي نظرية تكاملية حول توسيع دالة تحليلية في سلسلة قوى. يستخدم لابلاس متغيرات معقدة لحساب التكاملات الصعبة ويطور طريقة لحل المعادلات الخطية والفرق والتفاضلية المعروفة باسم تحويل لابلاس.
منذ عام 1799 ، تظهر الأعمال التي يتم فيها تقديم تفسيرات أكثر أو أقل ملاءمة لعدد معقد ويتم تحديد الإجراءات عليها. تم نشر التفسير النظري العام إلى حد ما والتفسير الهندسي بواسطة K.Gauss فقط في عام 1831.
ترك ل. أويلر ومعاصروه إرثًا ثريًا لأحفادهم في شكل حقائق متراكمة ، منظمة في مكان ما ، في مكان ما لا ، لكنها لا تزال مبعثرة على TFKP. يمكننا القول أن المادة الواقعية حول وظائف الكميات التخيلية ، كما كانت ، تتطلب تنظيمها في شكل نظرية. بدأت هذه النظرية في تشكيلها.
المرحلة الثالثة في تشكيل TFKP (القرن التاسع عشر - القرن العشرين). المزايا الرئيسية هنا تنتمي إلى O. Cauchy (1789-1857) ، B. Riemann (1826-1866) ، و K. Weierstrass (1815-1897). يمثل كل منهم أحد اتجاهات تطوير TFKP.
كان ممثل الاتجاه الأول ، والذي كان يُطلق عليه في تاريخ الرياضيات "نظرية الوظائف أحادية الجين أو الوظائف القابلة للتفاضل" هو O. Cauchy. قام بصياغة الحقائق المبعثرة حول حساب التفاضل والتكامل لوظائف متغير معقد ، وأوضح معنى المفاهيم الأساسية والعمليات ذات المفاهيم التخيلية. شرح O. Cauchy نظرية الحدود ونظرية السلاسل والوظائف الأولية المبنية عليها ، وصاغ نظرية توضح تمامًا مجال تقارب سلسلة الطاقة. في عام 1826 ، قدم O. Cauchy المصطلح: الخصم (حرفيًا: الباقي). في كتاباته من 1826 إلى 1829 ، ابتكر نظرية الاستقطاعات. اشتق O. Cauchy صيغة متكاملة ؛ حصلنا على نظرية وجود لتوسيع دالة لمتغير معقد في سلسلة القدرة (1831). وضع O. Cauchy أسس نظرية الوظائف التحليلية لعدة متغيرات ؛ تحديد الفروع الرئيسية للوظائف متعددة القيم لمتغير معقد ؛ استخدمت لأول مرة عمليات قطع الطائرات (1831-1847). في عام 1850 ، قدم مفهوم الوظائف أحادية اللون ، وميز فئة الوظائف أحادية المنشأ.
كان أحد أتباع O. Cauchy هو B. Riemann ، الذي أنشأ أيضًا اتجاهه "الهندسي" (الثاني) لتطوير TFKP. في أعماله ، تغلب على عزل الأفكار حول وظائف المتغيرات المعقدة وشكل أقسامًا جديدة لهذه النظرية ، ترتبط ارتباطًا وثيقًا بالتخصصات الأخرى. اتخذ ريمان خطوة جديدة مهمة في تاريخ نظرية الوظائف التحليلية ، واقترح ربط كل وظيفة لمتغير معقد بتمثيل تخطيط منطقة إلى أخرى. أسس التمييز بين وظائف المتغير المعقد والحقيقي. قام ب.
حدث مزيد من التطوير لـ TFKP في اتجاه مختلف (ثالث). كان أساسها إمكانية تمثيل الوظائف بواسطة سلسلة الطاقة. إن الاسم "التحليلي" عالق في التاريخ لهذا الاتجاه. تم تشكيلها في أعمال K. Weierstrass ، حيث أبرز مفهوم التقارب الموحد. صاغ K. Weierstrass وأثبت نظرية حول شرعية اختزال المصطلحات المماثلة في سلسلة. حصل K. Weierstrass على نتيجة أساسية: حد سلسلة من الوظائف التحليلية المتقاربة بشكل موحد داخل مجال معين هي وظيفة تحليلية. كان قادرًا على تعميم نظرية كوشي على التوسع في سلسلة القدرة لوظيفة متغير معقد ووصف عملية الاستمرار التحليلي لسلسلة القدرة وتطبيقها على تمثيل حلول نظام المعادلات التفاضلية. أنشأ K. Weierstrass حقيقة ليس فقط التقارب المطلق للسلسلة ، ولكن أيضًا التقارب المنتظم. تظهر نظرية Weierstrass عند توسيع دالة كاملة إلى منتج. يضع أسس نظرية الوظائف التحليلية للعديد من المتغيرات ، ويبني نظرية قابلية القسمة على سلسلة القوى.
ضع في اعتبارك تطوير نظرية الوظائف التحليلية في روسيا. علماء الرياضيات الروس في القرن التاسع عشر. لفترة طويلة لم يرغبوا في تكريس أنفسهم لمجال جديد من الرياضيات. على الرغم من ذلك ، يمكن للمرء تسمية عدة أسماء لم تكن غريبة عنها ، وسرد بعض أعمال وإنجازات علماء الرياضيات الروس هؤلاء.
كان أحد علماء الرياضيات الروس M.V. أوستروجرادسكي (1801-1861). حول بحث M.V. لا يُعرف الكثير عن Ostrogradskii في مجال نظرية الوظائف التحليلية ، ولكن أشاد O. Cauchy بهذا العالم الروسي الشاب ، الذي طبق التكاملات وقدم أدلة جديدة على الصيغ وعمم الصيغ الأخرى. م. كتب أوستروجرادسكي ورقة بعنوان "ملاحظات على التكاملات المحددة" ، اشتق فيها صيغة كوشي لاستنتاج دالة فيما يتعلق بقطب من الترتيب التاسع. أوجز تطبيق نظرية البقايا ومعادلة كوشي لحساب التكاملات المحددة في دورة محاضرة عامة مكثفة عُقدت في 1858-1859.
عدد من الأعمال من قبل N.I. Lobachevsky ، والتي لها أهمية مباشرة لنظرية وظائف المتغير المعقد. نظرية الدوال الأولية لمتغير معقد واردة في عمله "الجبر أو حساب المنتهية" (كازان ، 1834). حيث يتم تحديد cos x و sin x مبدئيًا لـ x حقيقي على أنه حقيقي و
الجزء التخيلي للدالة مثل ^. باستخدام الخصائص المحددة مسبقًا للدالة الأسية وتوسعات القوة ، يتم اشتقاق جميع الخصائص الأساسية للوظائف المثلثية. بواسطة-
على ما يبدو ، أولى Lobachevsky أهمية خاصة لمثل هذا البناء التحليلي البحت لعلم المثلثات ، بغض النظر عن الهندسة الإقليدية.
يمكن القول أنه في العقود الأخيرة من القرن التاسع عشر. والعقد الأول من القرن العشرين. يتكون البحث الأساسي في نظرية وظائف المتغير المعقد (F. Klein ، A. Poincaré ، P. Kebe) في التوضيح التدريجي لحقيقة أن هندسة Lobachevsky هي في نفس الوقت هندسة الوظائف التحليلية لمجمع واحد عامل.
في عام 1850 ، عمل أستاذ بجامعة سانت بطرسبرغ (أكاديمي لاحقًا) I.I. نشر سوموف (1815-1876) أسس نظرية الوظائف التحليلية ، والتي كانت مبنية على أسس جاكوبي الجديدة.
ومع ذلك ، كان يو.ف. سوخوتسكي (1842-1929). دافع عن أطروحة الماجستير "نظرية المخلفات المتكاملة مع بعض التطبيقات" (سانت بطرسبرغ ، 1868). منذ خريف عام 1868 ، بدأ Yu.V. أعطى Sokhotsky دورات حول نظرية وظائف المتغير التخيلي والكسور المستمرة مع تطبيقات للتحليل. أطروحة الماجستير Yu.V. Sokhotskii مكرس لتطبيقات نظرية البقايا لعكس سلسلة الطاقة (سلسلة لاغرانج) ، وعلى وجه الخصوص ، لتوسيع الوظائف التحليلية في الكسور المستمرة ، وكذلك ليجيندر متعدد الحدود. في هذه الورقة ، تمت صياغة النظرية الشهيرة حول سلوك وظيفة تحليلية في حي من نقطة مفردة بشكل أساسي وإثباتها. أطروحة الدكتوراه Sokhotskiy
(1873) قدم لأول مرة في شكل موسع مفهوم التكامل من نوع كوشي: * y ^ & _ where
a و b رقمان مركبان عشوائيان. من المفترض أن يتم أخذ التكامل على طول منحنى ("مسار") يربط أ و ب. في هذه الورقة ، تم إثبات عدد من النظريات.
لعبت أعمال N.E. دورًا كبيرًا في تاريخ الوظائف التحليلية. جوكوفسكي و S.A. Chaplygin ، الذي اكتشف المنطقة اللامحدودة لتطبيقاته في الديناميكا الهوائية والميكانيكا المائية.
عند الحديث عن تطور نظرية الوظائف التحليلية ، لا يسع المرء إلا أن يذكر دراسات S.V. Kovalevskaya ، على الرغم من أن أهميتها الرئيسية تكمن خارج حدود هذه النظرية. يرجع نجاح عملها إلى صياغة جديدة تمامًا للمشكلة من حيث نظرية الوظائف التحليلية واعتبار الوقت t كمتغير معقد.
في مطلع القرن العشرين. تتغير طبيعة البحث العلمي في مجال نظرية وظائف المتغير المعقد. إذا تم إجراء معظم البحث في وقت سابق في هذا المجال من حيث تطوير أحد الاتجاهات الثلاثة (نظرية وظائف كوشي أحادية المنشأ أو القابلة للتفاضل ، والأفكار الهندسية والفيزيائية لريمان ، والاتجاه التحليلي لـ Weierstrass) ، والآن الاختلافات يتم التغلب على النزاعات ذات الصلة ، وهناك ويتزايد بسرعة عدد الأعمال التي يتم فيها تجميع الأفكار والأساليب. أحد المفاهيم الأساسية التي تم الكشف عنها بوضوح عن اتصال ومراسلات التمثيلات الهندسية وجهاز سلسلة الطاقة هو مفهوم الاستمرارية التحليلية.
في نهاية القرن التاسع عشر. تتضمن نظرية وظائف المتغير المعقد مجموعة واسعة من التخصصات: النظرية الهندسية للوظائف القائمة على نظرية التعيينات المطابقة وأسطح ريمان. لقد حصلنا على صيغة متكاملة لنظرية أنواع مختلفة من الوظائف: كاملة ومحددة الشكل ، إهليلجية ونمطية ، ذات شكل آلي ، متناسق ، جبري. في اتصال وثيق مع الفئة الأخيرة من الوظائف ، تم تطوير نظرية تكاملات أبيليان. كانت النظرية التحليلية للمعادلات التفاضلية والنظرية التحليلية للأرقام ملاصقة لهذا المركب. أنشأت نظرية الوظائف التحليلية الروابط مع التخصصات الرياضية الأخرى وعززتها.
ساهم ثراء العلاقات المتبادلة لـ TFKP مع الجبر والهندسة والعلوم الأخرى ، وإنشاء الأسس المنهجية لعلم TFKP نفسه ، وأهميته العملية الكبيرة في تشكيل TFKP كموضوع أكاديمي. ومع ذلك ، بالتزامن مع الانتهاء من تشكيل الأسس ، تم إدخال أفكار جديدة في نظرية الوظائف التحليلية ، مما أدى إلى تغيير كبير في تكوينها وطبيعتها وأهدافها. تظهر الدراسات التي تحتوي على عرض منهجي لنظرية الوظائف التحليلية بأسلوب قريب من البديهية ولها أيضًا أهداف تعليمية. على ما يبدو ، فإن أهمية النتائج على TFKP ، التي حصل عليها علماء الفترة قيد المراجعة ، دفعتهم إلى الترويج لـ TFKP في شكل إلقاء المحاضرات ونشر الدراسات الفردية في منظور تعليمي. يمكن أن نستنتج أن TFKP ظهرت كمؤسسة تعليمية
موضوعات. في عام 1856 ، نشر كل من سي بريوت وت. بوكيه مذكرات قصيرة بعنوان "التحقيق في وظائف متغير وهمي" ، وهي في الأساس أول كتاب مدرسي. بدأ تطوير المفاهيم العامة في نظرية وظائف المتغير المعقد في المحاضرات. منذ عام 1856 قدم K. Weierht-rass محاضرات حول تمثيل الوظائف من خلال سلسلة القوة المتقاربة ، ومنذ عام 1861 - حول النظرية العامة للوظائف. في عام 1876 ، ظهر عمل خاص لـ K. Weierstrass: "حول نظرية الوظائف التحليلية أحادية القيمة" ، وفي عام 1880 "حول عقيدة الوظائف" ، حيث اكتسبت نظريته للوظائف التحليلية قدرًا معينًا من الاكتمال.
خدمت محاضرات Weierstrass لسنوات عديدة كنموذج أولي للكتب المدرسية حول نظرية وظائف المتغير المعقد ، والتي بدأت تظهر كثيرًا منذ ذلك الحين. في محاضراته تم بناء المعيار الحديث للصرامة في التحليل الرياضي وتم تسليط الضوء على الهيكل الذي أصبح تقليديًا.
قائمة ببليوغرافية
1. أندرونوف إ. ك. رياضيات الأعداد الحقيقية والمركبة. موسكو: التعليم ، 1975.
2. Klein F. محاضرات عن تطور الرياضيات في القرن التاسع عشر. موسكو: ONTI ، 1937. الجزء الأول.
3. Lavrent'ev M.A.، Shabat B.V. طرق نظرية وظائف المتغير المعقد. موسكو: Nauka ، 1987.
4. Markushevich A.I. نظرية الوظائف التحليلية. م: الدولة. دار نشر الأدب الفني والنظري 1950.
5. رياضيات القرن التاسع عشر. الهندسة. نظرية الدوال التحليلية / إد. A.N. Kolmogorov و A.P. Yushkevich. موسكو: Nauka ، 1981.
6. الموسوعة الرياضية / الفصل. إد. آي إم فينوغرادوف. موسكو: الموسوعة السوفيتية ، 1977.Vol.1.
7. موسوعة الرياضيات / الفصل. إد. آي إم فينوغرادوف. موسكو: الموسوعة السوفيتية ، 1979 ، المجلد 2.
8. يونغ ف. أساسيات عقيدة العدد في القرن الثامن عشر وأوائل القرن التاسع عشر. م: أوشبيدجيز ، 1963.
9. Rybnikov K.A. تاريخ الرياضيات. موسكو: دار نشر جامعة موسكو الحكومية ، 1963. الجزء الثاني.
ليس. منحنيات طائرة Lyakhova الملموسة
مسألة تماس منحنيات المستوى ، في حالة العثور على حدود النقاط المشتركة من معادلة بالصيغة Pn x = 0 ، حيث P x هي بعض كثيرة الحدود ، ترتبط ارتباطًا مباشرًا بالسؤال
على تعدد جذور كثير الحدود Pn x. في هذه المقالة ، تمت صياغة البيانات المقابلة لحالات التخصيص الصريح والضمني للوظائف التي تكون رسومها البيانية منحنيات ، ويتم عرض تطبيق هذه العبارات في حل المشكلات.
إذا كانت المنحنيات التي تمثل الرسوم البيانية للوظائف y = f (x) و y = cp x لها نقطة مشتركة
م () × 0 ؛ v0 ، أي y0 = f x0 = cp x0 وظلال المنحنيات المشار إليها المرسومة عند النقطة M () x0 ؛ v0 لا تتطابق ، ثم يقولون أن المنحنيات y = fix) و y - cp x تتقاطع عند النقطة Mo xo ؛ Yo
يوضح الشكل 1 مثالاً على تقاطع الرسوم البيانية للوظائف.
هذا هو اسم نوع آخر من التحويلات التكاملية ، والتي ، إلى جانب تحويل فورييه ، تُستخدم على نطاق واسع في الهندسة الراديوية لحل مجموعة متنوعة من المشكلات المتعلقة بدراسة الإشارات.
مفهوم التردد المعقد.
تعتمد الطرق الطيفية ، كما هو معروف بالفعل ، على حقيقة أن الإشارة قيد التحقيق يتم تمثيلها كمجموع لعدد غير محدود من المصطلحات الأولية ، كل منها يتغير بشكل دوري في الوقت وفقًا للقانون.
يكمن التعميم الطبيعي لهذا المبدأ في حقيقة أنه بدلاً من الإشارات الأسية المعقدة ذات المؤشرات الخيالية البحتة ، يتم تقديم الإشارات الأسية للنموذج في الاعتبار ، حيث يوجد رقم معقد: يسمى التردد المعقد.
يمكن استخدام اثنتين من هذه الإشارات المعقدة لتكوين إشارة حقيقية ، على سبيل المثال ، وفقًا للقاعدة التالية:
أين هي القيمة المرافقة المعقدة.
في الواقع ، في هذه الحالة
![]()
اعتمادًا على اختيار الأجزاء الحقيقية والخيالية للتردد المعقد ، يمكن الحصول على إشارات حقيقية مختلفة. لذلك ، إذا ، لكنك حصلت على تذبذبات توافقية عادية للنموذج ، إذن ، بناءً على العلامة ، تحصل على تذبذبات أسية متزايدة أو متناقصة في الوقت المناسب. تكتسب هذه الإشارات شكلاً أكثر تعقيدًا عندما. هنا ، يصف المضاعف مغلفًا يتغير أسيًا بمرور الوقت. بعض الإشارات النموذجية موضحة في الشكل. 2.10.
تبين أن مفهوم التردد المعقد مفيد جدًا ، أولاً وقبل كل شيء ، لأنه يجعل من الممكن ، دون اللجوء إلى الوظائف المعممة ، الحصول على تمثيلات طيفية للإشارات التي لا يمكن دمج نماذجها الرياضية.

أرز. 2.10. الإشارات الحقيقية المقابلة لقيم مختلفة للتردد المعقد
هناك اعتبار آخر ضروري أيضًا: تعمل الإشارات الأسية من النموذج (2.53) كوسيلة "طبيعية" لدراسة التذبذبات في مجموعة متنوعة من الأنظمة الخطية. سيتم استكشاف هذه الأسئلة في الفصل. ثمانية.
وتجدر الإشارة إلى أن التردد المادي الحقيقي هو الجزء التخيلي للتردد المعقد. لا يوجد مصطلح خاص للجزء الحقيقي من التردد المعقد.
العلاقات الأساسية.
يجب أن تكون بعض الإشارات ، حقيقية أو معقدة ، محددة عند t> 0 وتساوي الصفر في قيم الوقت السالبة. تحويل لابلاس لهذه الإشارة هو دالة لمتغير معقد يعطى بواسطة تكامل:

تسمى الإشارة الأصلية ، وتسمى الوظيفة صورة لابلاس (باختصار ، الصورة فقط).
الشرط الذي يضمن وجود التكامل (2.54) هو كما يلي: يجب ألا تحتوي الإشارة على أكثر من معدل نمو أسي ، أي يجب أن تفي بعدم المساواة حيث تكون الأرقام موجبة.
عندما يتم استيفاء هذه المتباينة ، توجد الوظيفة بمعنى أن التكامل (2.54) يتقارب تمامًا لجميع الأعداد المركبة التي يُطلق عليها الرقم أ حد التقارب المطلق.
يمكن تحديد المتغير في الصيغة الرئيسية (2.54) بالتردد المعقد بالفعل ، بتردد معقد وهمي بحت ، عندما تتحول الصيغة (2.54) إلى صيغة (2.16) ، والتي تحدد تحويل فورييه للإشارة ، وهو صفر عند وبالتالي ، يمكن اعتبار تحويل لابلاس
تمامًا كما يحدث في نظرية تحويل فورييه ، من الممكن ، بمعرفة الصورة ، استعادة الأصل. لهذا ، في معكوس صيغة تحويل فورييه

يجب إجراء استمرار تحليلي ، بالمرور من المتغير التخيلي إلى الوسيطة المعقدة أ. على مستوى التردد المعقد ، يتم تنفيذ التكامل على طول محور عمودي ممتد بشكل لا نهائي يقع على يمين الحد الفاصل للتقارب المطلق. نظرًا لأن at هو التفاضل ، فإن صيغة تحويل لابلاس العكسي تأخذ الشكل

في نظرية وظائف المتغير المعقد ، ثبت أن صور لابلاس لها خصائص "جيدة" من وجهة نظر النعومة: مثل هذه الصور في جميع نقاط المستوى المعقد ، باستثناء مجموعة قابلة للعد مما يسمى نقاط المفرد ، هي وظائف تحليلية. النقاط الفردية ، كقاعدة عامة ، هي أقطاب ، مفردة أو متعددة. لذلك ، لحساب تكاملات النموذج (2.55) ، يمكن استخدام طرق مرنة لنظرية البقايا.
من الناحية العملية ، تُستخدم جداول تحويل لابلاس على نطاق واسع ، والتي تجمع معلومات حول المراسلات بين الأصول. والصور. أدى وجود الجداول إلى جعل طريقة تحويل لابلاس شائعة في كل من الدراسات النظرية والحسابات الهندسية لأجهزة وأنظمة الهندسة الراديوية. يوجد في الملاحق مثل هذا الجدول الذي يسمح لك بحل مجموعة واسعة من المشاكل.
أمثلة على حساب تحويلات لابلاس.
تشترك طرق حساب الصور كثيرًا مع ما تمت دراسته بالفعل فيما يتعلق بتحويل فورييه. دعونا ننظر في الحالات الأكثر شيوعًا.
مثال 2.4 ، صورة للزخم الأسي المعمم.
اسمحوا ، أين هو رقم مركب ثابت. وجود الدالة - يحدد المساواة عند استخدام الصيغة (2.54) ، لدينا

إذا اختفى البسط عند استبدال الحد الأعلى. نتيجة لذلك ، نحصل على المراسلات
![]()
كحالة خاصة للصيغة (2.56) ، يمكنك العثور على صورة لنبض فيديو أسي حقيقي:
![]()
وإشارة أسية معقدة:
![]()
أخيرًا ، بوضع (2.57) ، نجد صورة وظيفة Heaviside:
مثال 2.5. صورة دالة دلتا.
تحويل لابلاس- تحويل متكامل يربط الوظيفة و (ث) (displaystyle F (s))متغير معقد ( صورة) مع الوظيفة و (س) (displaystyle f (x))متغير حقيقي ( أصلي). بمساعدتها ، يتم التحقيق في خصائص الأنظمة الديناميكية ويتم حل المعادلات التفاضلية والتكاملية.
تتمثل إحدى ميزات تحويل لابلاس ، التي حددت مسبقًا استخدامه على نطاق واسع في الحسابات العلمية والهندسية ، في أن العديد من النسب والعمليات على النسخ الأصلية تتوافق مع نسب أبسط على صورها. وبالتالي ، يتم تقليل الالتواء بين وظيفتين في مساحة الصورة إلى عملية الضرب ، وتصبح المعادلات التفاضلية الخطية جبرية.
كليات يوتيوب
1 / 5
✪ تحويل لابلاس - bezbotvy
المحاضرة 10: تحويل لابلاس
الرياضيات العليا - 4. تحويل لابلاس. الجزء 1
طريقة لابلاس لحل المعادلات التفاضلية
المحاضرة 11: تطبيق تحويل لابلاس على حل المعادلات التفاضلية
ترجمات
تعريف
تحويل لابلاس المباشر
ليم ب → ∞ ∫ 0 ب | و (س) | ه - σ 0 س د س = ∫ 0 ∞ | و (س) | هـ - σ 0 س دكس، (displaystyle lim _ (b to infty) int limits _ (0) ^ (b) | f (x) | e ^ (- sigma _ (0) x) ، dx = \ int \ limits _ (0) ^ (\ infty) | f (x) | e ^ (- \ sigma _ (0) x) \ ، dx ،)ثم تتقارب بشكل مطلق وموحد من أجل وهي وظيفة تحليلية لـ σ ⩾ σ 0 (displaystyle sigma geqslant sigma _ (0)) (σ = R. e ث (displaystyle sigma = mathrm (Re) ، s)- جزء حقيقي من متغير معقد ث (displaystyle s)). حافة سفلية دقيقة σ أ (displaystyle sigma _ (a))مجموعات من الأرقام σ (displaystyle sigma)، والتي بموجبها يتم استيفاء هذا الشرط ، يسمى الحد الأقصى للتقارب المطلقتحويل لابلاس للوظيفة.
- شروط وجود تحويل لابلاس المباشر
تحويل لابلاس L (f (x)) (displaystyle (mathcal (L)) (f (x)))يوجد بمعنى التقارب المطلق في الحالات التالية:
- σ ⩾ 0 (displaystyle sigma geqslant 0): يوجد تحويل لابلاس إذا كان هناك جزء لا يتجزأ ∫ 0 ∞ | و (س) | د س (displaystyle int limits _ (0) ^ (infty) | f (x) | ، dx);
- σ> σ أ (displaystyle sigma> sigma _ (a)): تحويل لابلاس موجود إذا كان التكامل ∫ 0 × 1 | و (س) | د س (displaystyle int limits _ (0) ^ (x_ (1)) | f (x) | ، dx)موجود لكل نهاية x 1> 0 (\ displaystyle x_ (1)> 0)و | و (س) | ⩽ البوتاسيوم ه σ أ س (displaystyle | f (x) | leqslant Ke ^ (sigma _ (a) x))ل x> x 2 ⩾ 0 (displaystyle x> x_ (2) geqslant 0);
- σ> 0 (\ displaystyle \ sigma> 0)أو σ> σ أ (displaystyle sigma> sigma _ (a))(أي من الحدود أكبر): يوجد تحويل لابلاس إذا كان هناك تحويل لابلاس للوظيفة و ′ (س) (displaystyle f "(x))(مستمدة من و (س) (displaystyle f (x))) ل σ> σ أ (displaystyle sigma> sigma _ (a)).
ملحوظة
- شروط وجود تحويل لابلاس المعكوس
لوجود تحويل لابلاس معكوس ، الشروط التالية كافية:
- إذا كانت الصورة و (ث) (displaystyle F (s))- الوظيفة التحليلية ل σ ⩾ σ أ (displaystyle sigma geqslant sigma _ (a))ولها ترتيب أقل من 1 ، فإن التحويل العكسي لها موجود ومستمر لجميع قيم الوسيطة ، و L - 1 (F (s)) = 0 (displaystyle (mathcal (L)) ^ (- 1) (F (s)) = 0)ل تي ⩽ 0 (displaystyle t leqslant 0).
- اسمحوا ان F (s) = φ [F 1 (s)، F 2 (s)، ...، F n (s)] (displaystyle F (s) = varphi)، وبالتالي φ (z 1، z 2، ...، z n) (displaystyle varphi (z_ (1)، \؛ z_ (2)، \؛ ldots،؛ z_ (n)))تحليلي عن كل منهما ض ك (displaystyle z_ (k))ويساوي صفرًا ل ض 1 = ض 2 = ... = ض n = 0 (displaystyle z_ (1) = z_ (2) = ldots = z_ (n) = 0)، و و ك (ث) = L (fk (x)) (σ> σ ak: k = 1، 2،…، n) (displaystyle F_ (k) (s) = (mathcal (L)) (f_ (ك) (س) \) \ ؛ \ ؛ (\ سيغما> \ سيجما _ (ak) \ القولون ك = 1 ، \ ؛ 2 ، \ ؛ \ ldots ، \ ؛ n))، ثم التحويل العكسي موجود والتحويل الأمامي المقابل له حد التقارب المطلق.
ملحوظة: هذه شروط كافية للوجود.
- نظرية الالتواء
مقالة مفصلة: نظرية الالتواء
- تفريق ودمج الأصل
صورة لابلاس للمشتق الأول من الأصل فيما يتعلق بالحجة هي نتاج الصورة بحجة الأخير مطروحًا منها الأصل عند الصفر على اليمين:
L (f ′ (x)) = s ⋅ F (s) - f (0 +). (displaystyle (mathcal (L)) (f "(x)) = s cdot F (s) -f (0 ^ (+)).)نظريات القيمة الأولية والنهائية (مبرهنات التحديد):
و (∞) = lim s → 0 ث F (ث) (displaystyle f (infty) = lim _ (s to 0) sF (s))إذا كانت جميع أقطاب الوظيفة ث و (ث) (displaystyle sF (s))تقع في النصف الأيسر من المستوى.نظرية القيمة المحدودة مفيدة للغاية لأنها تصف سلوك الأصل عند اللانهاية باستخدام علاقة بسيطة. يستخدم هذا ، على سبيل المثال ، لتحليل استقرار مسار النظام الديناميكي.
- خصائص أخرى
الخطية:
L (a f (x) + b g (x)) = a F (s) + b G (s). (displaystyle (mathcal (L)) (af (x) + bg (x)) = aF (s) + bG (s).)الضرب برقم:
L (f (a x)) = 1 a F (s a). (displaystyle (mathcal (L)) (f (ax)) = (frac (1) (a)) F left ((frac (s) (a)) right).)تحويل لابلاس المباشر والمعكوس لبعض الوظائف
يوجد أدناه جدول تحويل لابلاس لبعض الوظائف.
| № | وظيفة | المجال الزمني x (t) = L - 1 (X (s)) (displaystyle x (t) = (mathcal (L)) ^ (- 1) (X (s))) |
مجال التردد X (s) = L (x (t)) (displaystyle X (s) = (mathcal (L)) (x (t))) |
منطقة التقارب ل النظم السببية |
|---|---|---|---|---|
| 1 | تأخر تام | δ (t - τ) (displaystyle delta (t- tau)) | هـ - τ الصورة (displaystyle e ^ (- tau s)) | |
| 1 أ | دفعة واحدة | δ (t) (displaystyle delta (t)) | 1 (displaystyle 1) | ∀ ث (displaystyle forall s) |
| 2 | بطئ n (displaystyle n) | (ر - τ) ن ن! ه - α (t - τ) ⋅ H (t - τ) (displaystyle (frac ((t- tau) ^ (n)) (n}e^{-\alpha (t-\tau)}\cdot H(t-\tau)} !} | ه - τ ث (ث + α) n + 1 (displaystyle (frac (e ^ (- tau s)) ((s + alpha) ^ (n + 1)))) | ث> 0 (displaystyle s> 0) |
| 2 أ | رزين n (displaystyle n)الترتيب | ر ن ن! ⋅ H (t) (displaystyle (frac (t ^ (n)) (n}\cdot H(t)} !} | 1 ث n + 1 (displaystyle (frac (1) (s ^ (n + 1)))) | ث> 0 (displaystyle s> 0) |
| 2 أ -1 | رزين ف (displaystyle q)الترتيب | t q Γ (q + 1) ⋅ H (t) (displaystyle (frac (t ^ (q)) (Gamma (q + 1))) cdot H (t)) | 1 ث س + 1 (displaystyle (frac (1) (s ^ (q + 1)))) | ث> 0 (displaystyle s> 0) |
| 2 أ. 2 | وظيفة الوحدة | H (t) (displaystyle H (t)) | 1 ث (displaystyle (frac (1) (s))) | ث> 0 (displaystyle s> 0) |
| 2 ب | وظيفة وحدة التأخر | H (t - τ) (displaystyle H (t- tau)) | هـ - τ ث (displaystyle (frac (e ^ (- tau s)) (s))) | ث> 0 (displaystyle s> 0) |
| 2 ج | خطوة السرعة | t ⋅ H (t) (displaystyle t cdot H (t)) | 1 ث 2 (displaystyle (frac (1) (s ^ (2)))) | ث> 0 (displaystyle s> 0) |
| 2 د | n (displaystyle n)من الدرجة الثالثة مع تحول التردد | ر ن ن! هـ - α t ⋅ H (t) (\ displaystyle (\ frac (t ^ (n)) (n}e^{-\alpha t}\cdot H(t)} !} | 1 (ث + α) n + 1 (displaystyle (frac (1) ((s + alpha) ^ (n + 1)))) | ق> - α (displaystyle s> - alpha) |
| 2 د .1 | تسوس الأسي | هـ - α t ⋅ H (t) (displaystyle e ^ (- alpha t) cdot H (t)) | 1 ث + α (displaystyle (frac (1) (s + alpha))) | الصورة> - α (displaystyle s> - alpha) |
| 3 | التقريب الأسي | (1 - e - α t) ⋅ H (t) (displaystyle (1-e ^ (- alpha t)) cdot H (t)) | α ث (ث + α) (displaystyle (frac (alpha) (s (s + alpha)))) | ث> 0 (displaystyle s> 0) |
| 4 | التجويف | الخطيئة (ω t) ⋅ H (t) (displaystyle sin (omega t) cdot H (t)) | ω ث 2 + ω 2 (displaystyle (frac (omega) (s ^ (2) + omega ^ (2)))) | ث> 0 (displaystyle s> 0) |
| 5 | جيب التمام | كوس (ω t) ⋅ H (t) (displaystyle cos (omega t) cdot H (t)) | ث ث 2 + ω 2 (displaystyle (frac (s) (s ^ (2) + omega ^ (2)))) | ث> 0 (displaystyle s> 0) |
| 6 | الجيب الزائدي | ث ح (α t) ⋅ H (t) (displaystyle mathrm (sh) ، (alpha t) cdot H (t)) | α s 2 - α 2 (displaystyle (frac (alpha) (s ^ (2) - alpha ^ (2)))) | ق> | α | (displaystyle s> | alpha |) |
| 7 | جيب التمام الزائدي | ج ح (α t) ⋅ H (t) (displaystyle mathrm (ch) ، (alpha t) cdot H (t)) | ث ث 2 - α 2 (displaystyle (frac (s) (s ^ (2) - alpha ^ (2)))) | ق> | α | (displaystyle s> | alpha |) |
| 8 | اضعاف الاضمحلال التجويف |
هـ - α t sin (ω t) ⋅ H (t) (displaystyle e ^ (- alpha t) sin (omega t) cdot H (t)) | ω (ث + α) 2 + ω 2 (displaystyle (frac (omega) ((s + alpha) ^ (2) + omega ^ (2)))) | الصورة> - α (displaystyle s> - alpha) |
| 9 | اضعاف الاضمحلال جيب التمام |
هـ - α t cos (ω t) ⋅ H (t) (displaystyle e ^ (- alpha t) cos (omega t) cdot H (t)) | s + α (s + α) 2 + ω 2 (displaystyle (frac (s + alpha) ((s + alpha) ^ (2) + omega ^ (2)))) | الصورة> - α (displaystyle s> - alpha) |
| 10 | جذر n (displaystyle n)الترتيب | t n ⋅ H (t) (displaystyle (sqrt [(n)] (t)) cdot H (t)) | ث - (n + 1) / n ⋅ Γ (1 + 1 n) (displaystyle s ^ (- (n + 1) / n) cdot Gamma left (1 + (frac (1) (n) ) \ حق)) | ث> 0 (displaystyle s> 0) |
| 11 | اللوغاريتم الطبيعي | ln (t t 0) ⋅ H (t) (displaystyle ln left ((frac (t) (t_ (0))) right) cdot H (t)) | - t 0 ث [ln (t 0 ث) + γ] (displaystyle - (frac (t_ (0)) (s)) [ln (t_ (0) s) + gamma]) | ث> 0 (displaystyle s> 0) |
| 12 | دالة بيسل النوع الأول ترتيب n (displaystyle n) |
J n (ω t) ⋅ H (t) (displaystyle J_ (n) (omega t) cdot H (t)) | ω n (s + s 2 + ω 2) - ns 2 + ω 2 (\ displaystyle (\ frac (\ omega ^ (n) \ left (s + (\ sqrt (s ^ (2) + omega ^ (2 ))) \ right) ^ (- n)) (\ sqrt (s ^ (2) + \ omega ^ (2))))) | ث> 0 (displaystyle s> 0) (n> - 1) (displaystyle (n> -1)) |
| 13 | النوع الأول ترتيب n (displaystyle n) |
أنا n (ω t) ⋅ H (t) (displaystyle I_ (n) (omega t) cdot H (t)) | ω n (s + s 2 - ω 2) - ns 2 - ω 2 (\ displaystyle (\ frac (\ omega ^ (n) \ left (s + (\ sqrt (s ^ (2) - omega ^ (2 ))) \ right) ^ (- n)) (\ sqrt (s ^ (2) - \ omega ^ (2))))) | ق> | ω | (displaystyle s> | omega |) |
| 14 | دالة بيسل النوع الثاني طلب صفر |
Y 0 (α t) ⋅ H (t) (displaystyle Y_ (0) (alpha t) cdot H (t)) | - 2 أرش (ث / α) π الصورة 2 + α 2 (displaystyle - (frac (2 mathrm (arsh) (s / alpha)) (pi (sqrt (s ^ (2) + alpha ^ (2)))))) | ث> 0 (displaystyle s> 0) |
| 15 | تعديل دالة بيسل النوع الثاني طلب صفر |
البوتاسيوم 0 (α t) ⋅ H (t) (displaystyle K_ (0) (alpha t) cdot H (t)) | ||
| 16 | وظيفة الخطأ | ه r و (t) ⋅ H (t) (displaystyle mathrm (erf) (t) cdot H (t)) | ه ث 2/4 e r و ج (ق / 2) ث (displaystyle (frac (e ^ (s ^ (2) / 4) mathrm (erfc) (s / 2)) (s))) | ث> 0 (displaystyle s> 0) |
ملاحظات على الجدول:
| ||||
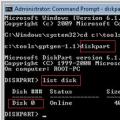 الاختلافات بين هياكل تقسيم GPT و MBR
الاختلافات بين هياكل تقسيم GPT و MBR امسح برنامج Internet Explorer نظيفًا
امسح برنامج Internet Explorer نظيفًا تم تنزيل تحديثات Windows ولكن لم يتم تثبيتها
تم تنزيل تحديثات Windows ولكن لم يتم تثبيتها