Zero della funzione secondo la pianificazione. Funzione zero. Regola della funzione zero
Funzioneè uno dei concetti matematici più importanti. Funzione: dipendenza dalle variabili a da una variabile X, se ogni valore X corrisponde a un singolo valore a. variabile X chiamato variabile o argomento indipendente. variabile a chiamata variabile dipendente. Tutti i valori della variabile indipendente (variabile X) formano il dominio della funzione. Tutti i valori che assume la variabile dipendente (variabile y), formano l'intervallo della funzione.
Grafico delle funzioni chiamano l'insieme di tutti i punti del piano delle coordinate, le cui ascisse sono uguali ai valori dell'argomento e le ordinate sono uguali ai valori corrispondenti della funzione, ovvero i valori di le variabili sono tracciate lungo l'asse delle ascisse X e i valori della variabile vengono tracciati lungo l'asse y y. Per tracciare una funzione, è necessario conoscere le proprietà della funzione. Le principali proprietà della funzione saranno discusse di seguito!
Per tracciare un grafico di funzione, ti consigliamo di utilizzare il nostro programma - Funzioni di rappresentazione grafica in linea. Se hai domande mentre studi il materiale in questa pagina, puoi sempre farle sul nostro forum. Inoltre sul forum verrai aiutato a risolvere problemi di matematica, chimica, geometria, teoria delle probabilità e molte altre materie!
Proprietà di base delle funzioni.
1) Ambito della funzione e gamma di funzioni.
L'ambito di una funzione è l'insieme di tutti i valori validi dell'argomento X(variabile X) per cui la funzione y = f(x) definito.
L'intervallo di una funzione è l'insieme di tutti i valori reali y che la funzione accetta.
Nella matematica elementare, le funzioni sono studiate solo sull'insieme dei numeri reali.
2) Funzione zeri.
Zero della funzione è il valore dell'argomento in cui il valore della funzione è uguale a zero.
3) Intervalli di costanza di segno di una funzione.
Gli intervalli di segno costante di funzione sono tali insiemi di valori di argomento su cui i valori di funzione sono solo positivi o solo negativi.
4) Monotonia della funzione.
Una funzione crescente (in un certo intervallo) è una funzione in cui un valore maggiore dell'argomento di questo intervallo corrisponde a un valore maggiore della funzione.
Funzione decrescente (in alcuni intervalli): una funzione in cui un valore maggiore dell'argomento da questo intervallo corrisponde a un valore minore della funzione.
5) Funzioni pari (dispari)..
Una funzione pari è una funzione il cui dominio di definizione è simmetrico rispetto all'origine e per qualsiasi X dal dominio di definizione l'uguaglianza f(-x) = f(x). Il grafico di una funzione pari è simmetrico rispetto all'asse y.
Una funzione dispari è una funzione il cui dominio di definizione è simmetrico rispetto all'origine e per qualsiasi X dal dominio di definizione l'uguaglianza f(-x) = - f(x). Il grafico di una funzione dispari è simmetrico rispetto all'origine.
6) Funzioni limitate e illimitate.
Una funzione si dice limitata se esiste un numero positivo M tale che |f(x)| ≤ M per tutti i valori di x . Se non esiste un tale numero, la funzione è illimitata.
7) Periodicità della funzione.
Una funzione f(x) è periodica se esiste un numero T diverso da zero tale che per ogni x f(x+T) = f(x). Questo numero più piccolo è chiamato periodo della funzione. Tutte le funzioni trigonometriche sono periodiche. (Formule trigonometriche).
Dopo aver studiato queste proprietà della funzione, è possibile esplorare facilmente la funzione e, utilizzando le proprietà della funzione, è possibile tracciare il grafico della funzione. Guarda anche il materiale sulla tavola della verità, la tavola delle moltiplicazioni, la tavola periodica, la tavola delle derivate e la tavola degli integrali.
Zero di funzione
Cosa sono gli zeri di funzione? Come determinare analiticamente e graficamente gli zeri di una funzione?
Zero di funzione sono i valori dell'argomento in cui la funzione è uguale a zero.
Per trovare gli zeri della funzione data dalla formula y=f(x), dobbiamo risolvere l'equazione f(x)=0.
Se l'equazione non ha radici, la funzione non ha zeri.
1) Trova gli zeri della funzione lineare y=3x+15.
Per trovare gli zeri della funzione, risolviamo l'equazione 3x+15 =0.
Quindi lo zero della funzione è y=3x+15 - x= -5 .
2) Trova gli zeri della funzione quadratica f(x)=x²-7x+12.
Per trovare gli zeri della funzione, risolviamo l'equazione quadratica
Le sue radici x1=3 e x2=4 sono gli zeri di questa funzione.
3) Trova gli zeri della funzione
Una frazione ha senso se il denominatore è diverso da zero. Pertanto, x²-1≠0, x² ≠ 1,x ≠±1. Cioè, il dominio di definizione di questa funzione (ODZ)
Dalle radici dell'equazione x²+5x+4=0 x1=-1 x2=-4, solo x=-4 è incluso nel dominio di definizione.
Per trovare gli zeri di una funzione data graficamente, è necessario trovare i punti di intersezione del grafico della funzione con l'asse x.
Se il grafico non attraversa l'asse Ox, la funzione non ha zeri.
la funzione il cui grafico è mostrato in figura ha quattro zeri -
In algebra, il problema di trovare gli zeri di una funzione si verifica sia come compito indipendente che quando si risolvono altri problemi, ad esempio quando si studia una funzione, si risolvono le disuguaglianze, ecc.
www.algebraclass.ru
Regola della funzione zero
Concetti di base e proprietà delle funzioni
regola (legge di) conformità. Funzione monotona .
Funzioni limitate e illimitate. Continuo e
funzione discontinua . Funzioni pari e dispari.
Funzione periodica. Periodo di funzione.
Zero di funzione . Asintoto .
L'ambito e la portata della funzione. Nella matematica elementare, le funzioni sono studiate solo sull'insieme dei numeri reali R . Ciò significa che l'argomento della funzione può assumere solo quei valori reali per i quali è definita la funzione, ovvero . accetta anche solo valori reali. Molti X tutti i valori validi validi dell'argomento X, per cui la funzione y = F (X) è definito, chiamato ambito della funzione. Molti Y tutti valori reali y che la funzione accetta viene chiamata gamma di funzioni. Possiamo ora dare una definizione più precisa della funzione: regola (legge di) corrispondenza tra insiemi X e Y , di cui per ogni elemento dell'insieme X puoi trovare uno e un solo elemento dal set Y, è chiamata funzione .
Da questa definizione deriva che una funzione si considera data se:
- l'ambito della funzione è impostato X ;
— l'intervallo di valori della funzione è impostato Y ;
- è nota la regola (legge) della corrispondenza, e tale che per ciascuno
valori degli argomenti, è possibile trovare solo un valore di funzione.
Questo requisito di unicità della funzione è obbligatorio.
funzione monotona.
Se per due valori qualsiasi dell'argomento X 1 e X 2 della condizione X 2 > X 1 segue F (X 2) > F (X 1), quindi la funzione F (X) è chiamato crescente; se per qualcuno X 1 e X 2 della condizione X 2 > X 1 segue F (X 2)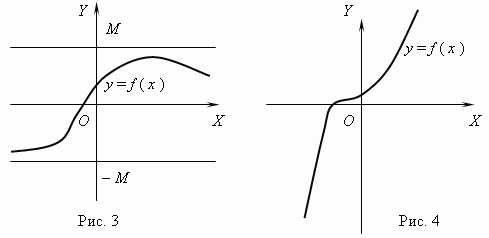 
La funzione rappresentata in Fig. 3 è limitata, ma non monotona. La funzione in Figura 4 è esattamente l'opposto, monotona ma illimitata. (Spiega questo per favore!)
Funzioni continue e discontinue. Funzione y = F (X) è chiamato continuo al punto X = un, Se:
1) la funzione è definita per X = un, cioè e. F (un) esiste;
2) esiste finito limite lim F (X) ;
Se almeno una di queste condizioni non è soddisfatta, viene chiamata la funzione discontinuo al punto X = un .
Se la funzione è in continuo tutti punti del suo dominio di definizione, quindi si chiama funzione continua.
Funzioni pari e dispari. Se per qualunque X dall'ambito della definizione della funzione avviene: F (— X) = F (X), quindi viene chiamata la funzione Anche; se lo fa: F (— X) = — F (X), quindi viene chiamata la funzione strano. Grafico di una funzione pari simmetrico rispetto all'asse Y(Fig.5), un grafico di una funzione dispari Sim metrica sull'origine(Fig. 6).
Funzione periodica. Funzione F (X) — periodico se esiste diverso da zero numero T per che cosa qualunque X dall'ambito della definizione della funzione avviene: F (X + T) = F (X). Come meno il numero è chiamato periodo di funzione. Tutte le funzioni trigonometriche sono periodiche.
ESEMPIO 1. Dimostra quel peccato X ha un periodo di 2.
SOLUZIONE Sappiamo che il peccato ( x + 2 n) = peccato X, dove n= 0, ± 1, ± 2, …
Pertanto, aggiungendo 2 n all'argomento seno
cambia il suo valore e . C'è un altro numero con questo
Facciamo finta che P- un tale numero, ad es. uguaglianza:
valido per qualsiasi valore X. Ma poi è così
luogo e a X= / 2, cioè es.
peccato(/2 + P) = peccato / 2 = 1.
Ma secondo la formula di riduzione sin (/ 2 + P) = cos P. Quindi
dalle ultime due uguaglianze segue che cos P= 1, ma noi
Sappiamo che questo è vero solo per P = 2 n. Dal più piccolo
un numero diverso da zero su 2 nè 2 , quindi questo numero
e c'è un periodo peccato X. Allo stesso modo si dimostra che 2
è un periodo per cos X .
Dimostra che le funzioni si abbronzano X e gatto X avere un periodo.
Esempio 2. Quale numero è il periodo della funzione sin 2 X ?
Soluzione Considera il peccato 2 X= peccato(2 x + 2 n) = peccato [ 2 ( X + n) ] .
Lo vediamo in aggiunta n all'argomento X, non cambia
valore della funzione. Numero più piccolo diverso da zero
da nè , quindi questo è il periodo sin 2 X .
Funzioni nulle. Viene chiamato il valore dell'argomento per cui la funzione è uguale a 0 zero ( radice) funzioni. Una funzione può avere più zeri. Ad esempio, la funzione y = X (X + 1) (X- 3) ha tre zeri: X = 0, X = — 1, X= 3. Geometricamente funzione nulla – è l'ascissa del punto di intersezione del grafico della funzione con l'asse X .
La figura 7 mostra il grafico della funzione con zeri: X = un , X = B e X = C .
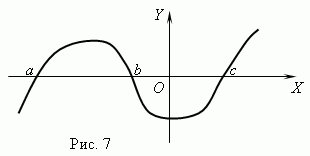
Asintoto. Se il grafico di una funzione si avvicina indefinitamente a una certa retta mentre si allontana dall'origine, allora questa retta è chiamata asintoto.
Argomento 6. "Metodo degli intervalli".
Se f (x) f (x 0) per x x 0, viene chiamata la funzione f (x). continuo a x 0.
Se una funzione è continua in ogni punto di un intervallo I, allora viene chiamata continuo sull'intervallo I (si chiama l'intervallo I intervallo di continuità della funzione). Il grafico della funzione su questo intervallo è una linea continua, che si dice sia "disegnata senza sollevare la matita dalla carta".
Proprietà delle funzioni continue.
Se sull'intervallo (a ; b) la funzione f è continua e non svanisce, allora mantiene un segno costante su questo intervallo.
Il metodo per risolvere le disuguaglianze con una variabile si basa su questa proprietà: il metodo degli intervalli. Sia la funzione f(x) continua sull'intervallo I e svanita in un numero finito di punti in questo intervallo. Per la proprietà delle funzioni continue, questi punti dividono I in intervalli, in ciascuno dei quali la funzione continua f(x) c custodisce un segno costante. Per determinare questo segno è sufficiente calcolare il valore della funzione f(x) in un punto qualsiasi di ciascuno di tali intervalli. Sulla base di ciò, otteniamo il seguente algoritmo per risolvere le disuguaglianze con il metodo dell'intervallo.
Il metodo dell'intervallo per le disuguaglianze del modulo
metodo dell'intervallo. Livello medio.
Vuoi mettere alla prova la tua forza e scoprire il risultato di quanto sei pronto per l'esame di stato unificato o l'OGE?
Funzione lineare
Una funzione della forma è chiamata lineare. Prendiamo una funzione come esempio. È positivo a 3″> e negativo a. Il punto è lo zero della funzione (). Mostriamo i segni di questa funzione sull'asse reale:
Diciamo che "la funzione cambia segno quando passa per un punto".
Si può notare che i segni della funzione corrispondono alla posizione del grafico della funzione: se il grafico è al di sopra dell'asse il segno è “ ”, se è al di sotto di esso “ ”.
Se generalizziamo la regola risultante a una funzione lineare arbitraria, otteniamo il seguente algoritmo:
funzione quadratica
Spero che ricordi come vengono risolte le disuguaglianze quadratiche? In caso contrario, leggere l'argomento "Disequazioni quadrate". Lascia che ti ricordi la forma generale di una funzione quadratica: .
Ora ricordiamo quali segni assume la funzione quadratica. Il suo grafico è una parabola e la funzione assume il segno “ ” per quelli in cui la parabola è sopra l'asse, e “ ” - se la parabola è sotto l'asse:
Se la funzione ha zeri (valori a cui), la parabola interseca l'asse in due punti: le radici dell'equazione quadratica corrispondente. Pertanto, l'asse è diviso in tre intervalli e i segni della funzione cambiano alternativamente quando si passa attraverso ciascuna radice.
È possibile determinare in qualche modo i segni senza disegnare ogni volta una parabola?
Ricordiamo che il trinomio quadrato può essere fattorizzato:
Nota le radici sull'asse:
Ricordiamo che il segno di una funzione può cambiare solo passando per la radice. Usiamo questo fatto: per ciascuno dei tre intervalli in cui l'asse è diviso per radici, è sufficiente determinare il segno della funzione solo in un punto scelto arbitrariamente: negli altri punti dell'intervallo il segno sarà il stesso.
Nel nostro esempio: per 3″> entrambe le espressioni tra parentesi sono positive (sostituiamo, ad esempio: 0″>). Mettiamo il segno "" sull'asse:
Ebbene, se (sostituendo, ad esempio) entrambe le parentesi sono negative, il prodotto è positivo:
Ecco cos'è metodo dell'intervallo: conoscendo i segni dei fattori su ciascun intervallo, determiniamo il segno dell'intero prodotto.
Consideriamo anche i casi in cui la funzione non ha zeri o è solo uno.
Se non ce ne sono, allora non ci sono radici. Ciò significa che non ci sarà alcun "passaggio attraverso la radice". Ciò significa che la funzione sull'intero asse numerico prende solo un segno. È facile da determinare sostituendolo in una funzione.
Se c'è una sola radice, la parabola tocca l'asse, quindi il segno della funzione non cambia quando si passa per la radice. Qual è la regola per tali situazioni?
Se escludiamo una tale funzione, otteniamo due fattori identici:
E qualsiasi espressione al quadrato non è negativa! Pertanto, il segno della funzione non cambia. In questi casi, selezioneremo la radice, passando attraverso la quale il segno non cambia, circondandola con un quadrato:
Tale radice sarà chiamata multiplo.
Il metodo degli intervalli nelle disuguaglianze
Ora qualsiasi disuguaglianza quadratica può essere risolta senza disegnare una parabola. Basta posizionare i segni della funzione quadratica sull'asse e scegliere gli intervalli in base al segno di disuguaglianza. Per esempio:
Misuriamo le radici sull'asse e disponiamo i segni:
Abbiamo bisogno della parte dell'asse con il segno ""; poiché la disuguaglianza non è rigorosa, nella soluzione sono incluse anche le radici stesse:
Consideriamo ora una disuguaglianza razionale - una disuguaglianza, le cui parti sono entrambe espressioni razionali (vedi "Equazioni razionali").
Esempio:
Tutti i fattori tranne uno - - qui sono "lineari", cioè contengono una variabile solo di primo grado. Abbiamo bisogno di tali fattori lineari per applicare il metodo dell'intervallo: il segno cambia quando passa attraverso le loro radici. Ma il moltiplicatore non ha affatto radici. Ciò significa che è sempre positivo (verificalo tu stesso) e quindi non intacca il segno dell'intera disuguaglianza. Ciò significa che puoi dividere i lati sinistro e destro della disuguaglianza in esso e quindi eliminarlo:
Ora tutto è come con le disuguaglianze quadratiche: determiniamo in quali punti svanisce ciascuno dei fattori, segniamo questi punti sull'asse e disponiamo i segni. Attiro la vostra attenzione su un fatto molto importante:
Nel caso di un numero pari, procediamo come prima: circondiamo il punto con un quadrato e non cambiamo il segno quando passiamo per la radice. Ma nel caso di un numero dispari, questa regola non è soddisfatta: il segno cambierà comunque passando per la radice. Pertanto, non facciamo nulla in più con una tale radice, come se non fosse un multiplo di noi. Le regole di cui sopra si applicano a tutte le potenze pari e dispari.
Cosa scriviamo nella risposta?
Se l'alternanza dei segni viene violata, devi stare molto attento, perché con disuguaglianza non rigorosa, la risposta dovrebbe includere tutti i punti pieni. Ma alcuni di loro spesso stanno da soli, cioè non entrano nell'area ombreggiata. In questo caso, li aggiungiamo alla risposta come punti isolati (tra parentesi graffe):
Esempi (decidi tu stesso):
Risposte:
- Se tra i fattori è semplice, questa è la radice, perché può essere rappresentata come.
.
dove assume il valore zero. Ad esempio, per una funzione data dalla formula
è nullo perché
.Vengono anche chiamati gli zeri di funzione radici di funzione.
Il concetto di zeri di una funzione può essere considerato per qualsiasi funzione il cui intervallo contenga zero o un elemento zero della corrispondente struttura algebrica.
Per una funzione di una variabile reale, gli zeri sono i valori a cui il grafico della funzione interseca l'asse x.
Trovare gli zeri di una funzione richiede spesso l'uso di metodi numerici (ad esempio il metodo di Newton, i metodi del gradiente).
Uno dei problemi matematici irrisolti è trovare gli zeri della funzione zeta di Riemann.
Radice polinomiale
Guarda anche
Letteratura
Fondazione Wikimedia. 2010.
Guarda cos'è "Funzione Zero" in altri dizionari:
Il punto in cui una data funzione f(z) svanisce; quindi, N. f. f (z) è la stessa delle radici dell'equazione f (z) = 0. Ad esempio, i punti 0, π, π, 2π, 2π,... sono gli zeri della funzione sinz. Zeri di una funzione analitica (Vedi Analitico ... ...
Funzione zero, funzione zero... Dizionario ortografico
Questo termine ha altri significati, vedi Zero. È necessario spostare il contenuto di questo articolo nell'articolo "Funzione Zero". Puoi aiutare il progetto consolidando gli articoli. Se hai bisogno di discutere dell'opportunità di unire, sostituisci questo ... Wikipedia
Oppure una stringa C (dal nome del linguaggio C) o una stringa ASCIZ (dal nome della direttiva assembler.asciz) è un modo per rappresentare stringhe nei linguaggi di programmazione, in cui viene utilizzata una matrice di caratteri invece di introdurre un tipo di stringa speciale e la fine ... ... Wikipedia
Nella teoria quantistica dei campi, il nome (gergale) accettato per la proprietà dell'annullamento del fattore di rinormalizzazione della costante di accoppiamento, dove g0 è la costante di accoppiamento nuda dall'interazione Lagrangiana, phys. costante di accoppiamento vestita dall'interazione. Uguaglianza Z... Enciclopedia fisica
Mutazione nulla n-allele- Mutazione nulla, n. allele * mutazione nulla, n. allele * mutazione nulla o n. allele o muto a. una mutazione che porta a una completa perdita di funzione nella sequenza del DNA in cui si è verificata ... Genetica. dizionario enciclopedico
L'affermazione nella teoria della probabilità che qualsiasi evento (il cosiddetto evento residuo), il cui verificarsi è determinato solo da elementi arbitrariamente remoti di una sequenza di eventi casuali indipendenti o variabili casuali, ha ... ... Enciclopedia matematica
1) Un numero che ha la proprietà che qualsiasi numero (reale o complesso) non cambia quando viene aggiunto ad esso. È indicato dal simbolo 0. Il prodotto di qualsiasi numero per N. è uguale a N.: Se il prodotto di due numeri è uguale a N., allora uno dei fattori ... Enciclopedia matematica
Funzioni date da relazioni tra variabili indipendenti non risolte rispetto a queste ultime; queste relazioni sono uno dei modi per definire una funzione. Ad esempio, la relazione x2 + y2 1 = 0 definisce il N. f. … Grande enciclopedia sovietica
Valori argomentativi z sotto il quale F(z) va a zero chiamato. punto zero, cioè. Se F(un) = 0 , allora a - punto zero.
def. Punto ma chiamata ordine zeron
, Se
FKP può essere rappresentato nel modulo F(z) = , dove 
funzione analitica e 
0.
In questo caso, nell'espansione della funzione in una serie di Taylor (43), la prima n i coefficienti sono zero
=
=
Eccetera. Determina l'ordine di zero per 
e (1-cos z) a z
=
0
=
=
zero 1° ordine
1 - cos z
=
=
zero 2° ordine
def. Punto z
=
chiamata punto all'infinito e zero funzioni F(z), Se F(
) = 0. Tale funzione si espande in una serie di potenze negative z
: F(z)
=
. Se
primo n
i coefficienti sono pari a zero, quindi si arriva a ordine zero n
in un punto all'infinito: F(z)
= z
-
n
.
I punti singolari isolati si dividono in: a) punti singolari rimovibili; B) ordinare i polin; in) punti singolari essenziali.
Punto ma chiamata punto singolare rimovibile funzioni F(z) Se z 
un
lim F(z)
= da - numero finito .
Punto ma chiamata polo dell'ordinen
(n
1) caratteristiche F(z) se la funzione inversa 
=
1/
F(z) ha ordine zero n al punto ma. Tale funzione può sempre essere rappresentata come F(z)
=
, dove 
- funzione analitica e 
.
Punto ma chiamata punto essenziale funzioni F(z), Se z 
un
lim F(z) non esiste.
serie Laurent
Consideriamo il caso di una regione di convergenza anulare R < | z 0 – un| < R centrato su un punto ma per funzione F(z). Introduciamo due nuovi cerchi l 1 (R) E l 2 (R) vicino ai confini dell'anello con un punto z 0 tra di loro. Facciamo una sezione dell'anello, uniamo i cerchi lungo i bordi della sezione, passiamo a una regione semplicemente collegata e in
Formula integrale di Cauchy (39) otteniamo due integrali sulla variabile z
F(z 0)
=
+
,
(42)
dove l'integrazione va in direzioni opposte.
Per l'integrale sopra l 1 la condizione | z 0 – un | > | z – un |, e per l'integrale over l 2 condizione inversa | z 0 – un | < | z – un |. Pertanto, il fattore 1/( z – z 0) espandere in una serie (a) nell'integrale sopra l 2 e nella serie (b) nell'integrale sopra l uno . Di conseguenza, otteniamo la decomposizione F(z) nella regione anulare in serie Laurent nei poteri positivi e negativi ( z 0 – un)
F(z 0)
=
UN n
(z 0 - un) n
(43)
dove UN n
=
=
;UN -n
=
Espansione dei poteri positivi (z 0 - ma) chiamata parte destra La serie Laurent (serie Taylor) e si chiama l'espansione nei poteri negativi. parte principale Fila Laurent.
Se all'interno del cerchio l 1 non ci sono punti singolari e la funzione è analitica, quindi in (44) il primo integrale è uguale a zero per il teorema di Cauchy, e nell'espansione della funzione rimane solo la parte corretta. I poteri negativi in espansione (45) compaiono solo quando l'analiticità è violata all'interno del cerchio interno e servono a descrivere la funzione vicino a punti singolari isolati.
Per costruire la serie Laurent (45) per F(z) si possono calcolare i coefficienti di dilatazione secondo la formula generale oppure utilizzare le espansioni delle funzioni elementari contenute in F(z).
Numero di termini ( n) della parte principale della serie Laurent dipende dal tipo di punto singolare: punto singolare rimovibile
(n
=
0)
; punto singolare essenziale
(n 
);
polon-esimo ordine(n
-
numero finale).
e per F(z)
=
punto z
= 0 punto singolare rimovibile, perché non c'è una parte principale. F(z)
=
(z
-
) = 1 -
b) Per F(z)
=
punto z
= 0 -
Palo di 1° ordine
F(z)
=
(z
-
) =
-
c) Per F(z) = e 1 / z punto z = 0 - punto singolare essenziale
F(z)
=
e 1 /
z =
Se F(z) è analitico nel dominio D con l'eccezione di m punti singolari isolati 
e | z 1 |
< |z 2 |
< . . . < |z m| , quindi quando si espande la funzione in poteri z l'intero piano è diviso in m+ 1 anello | z io |
< | z
| < | z io+ 1 | e la serie Laurent ha una forma diversa per ogni anello. Quando si espandono i poteri ( z
–
z io
) la regione di convergenza della serie di Laurent è il cerchio | z
–
z io
| < R, dove R
è la distanza dal punto singolare più vicino.
Eccetera. Espandi la funzione F(z)
=
nella serie di Laurent in poteri z E ( z
-
1).
Soluzione. Rappresentiamo la funzione nella forma F(z)
= - z 2
. Usiamo la formula per la somma di una progressione geometrica 
. Nel cerchio |z|< 1 ряд сходится и F(z)
= - z 2
(1 + z
+ z 2
+ z 3
+ z 4
+ . . .) = - z 2
- z 3
- z 4 - . . . , cioè. la decomposizione contiene solo corretta parte. Passiamo alla regione esterna del cerchio |z| > 1. Rappresentiamo la funzione nella forma 
, dove 1/| z|
< 1, и получим разложение F(z)
= z
=z
+ 1 +
Perché , ampliamento della funzione nei poteri ( z
-
1) sembra F(z)
= (z
-
1) -1
+ 2 + (z
-
1) per tutti 
1.
Eccetera. Espandi la funzione in una serie di Laurent F(z)
=
:
a) in gradi z in cerchio | z|
< 1; b)
по степеням z
anello 1<
|z|
< 3 ; c)
по степеням (z
–
2). Decisione. Scomponiamo la funzione in frazioni semplici
=
=
+
=
.
Dalle condizioni z
=1
UN
= -1/2 , z
=3
B
= ½.
ma) F(z)
=
½ [ 
]
= ½ [ 
-(1/3)
], quando | z|<
1.
B) F(z)
= - ½ [ 
+
]
= -
(
), a 1< |z|
< 3.
da) F(z)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, per |2 - z|
< 1
È una circonferenza di raggio 1 centrata su un punto z = 2 .
In alcuni casi, le serie di potenze possono essere ridotte a un insieme di progressioni geometriche, quindi è facile determinare l'area della loro convergenza.
Eccetera. Studiare la convergenza di una serie
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Soluzione. È la somma di due progressioni geometriche con Q 1
=
, Q 2 = () . Dalle condizioni della loro convergenza segue 
< 1 ,
< 1 или |z|
> 1 , |z|
< 2 , т.е. область сходимости ряда кольцо
1 < |z|
< 2 .
Cosa sono gli zeri di funzione? La risposta è abbastanza semplice: questo è un termine matematico, che indica il dominio di una determinata funzione, su cui il suo valore è zero. Gli zeri di funzione sono anche chiamati zeri di funzione Il modo più semplice per spiegare cosa sono gli zeri di funzione è con alcuni semplici esempi.
Esempi
Considera una semplice equazione y=x+3. Poiché lo zero della funzione è il valore dell'argomento in cui y diventa zero, sostituiamo 0 sul lato sinistro dell'equazione:
In questo caso, -3 è lo zero desiderato. Per una data funzione, esiste solo una radice dell'equazione, ma non è sempre così.
Considera un altro esempio:
Sostituisci 0 sul lato sinistro dell'equazione, come nell'esempio precedente:
Ovviamente, in questo caso, ci saranno due zeri della funzione: x=3 e x=-3. Se l'equazione avesse un argomento di terzo grado, ci sarebbero tre zeri. Possiamo trarre una semplice conclusione che il numero di radici del polinomio corrisponde al grado massimo dell'argomento nell'equazione. Tuttavia, molte funzioni, ad esempio y=x 3 , a prima vista contraddicono questa affermazione. La logica e il buon senso suggeriscono che questa funzione ha solo uno zero - nel punto x=0. Ma in realtà ci sono tre radici, semplicemente tutte coincidono. Se risolvi l'equazione in forma complessa, questo diventa ovvio. x=0 in questo caso la radice, la cui molteplicità è 3. Nell'esempio precedente, gli zeri non corrispondevano, quindi avevano una molteplicità di 1.
Algoritmo di definizione
Dagli esempi presentati è chiaro come determinare gli zeri della funzione. L'algoritmo è sempre lo stesso:
- Scrivi una funzione.
- Sostituisci y o f(x)=0.
- Risolvi l'equazione risultante.
La complessità dell'ultimo elemento dipende dal grado di argomentazione dell'equazione. Quando si risolvono equazioni di alto grado, è particolarmente importante ricordare che il numero di radici dell'equazione è uguale alla potenza massima dell'argomento. Ciò è particolarmente vero per le equazioni trigonometriche, dove la divisione di entrambe le parti per seno o coseno porta alla perdita delle radici.
Le equazioni di grado arbitrario sono risolte più facilmente con il metodo di Horner, che è stato sviluppato specificamente per trovare gli zeri di un polinomio arbitrario.
Il valore degli zeri delle funzioni può essere sia negativo che positivo, reale o giacente nel piano complesso, singolo o multiplo. Oppure potrebbero non esserci radici dell'equazione. Ad esempio, la funzione y=8 non diventerà zero per nessuna x, perché non dipende da questa variabile.
L'equazione y=x 2 -16 ha due radici, ed entrambe giacciono nel piano complesso: x 1 =4i, x 2 =-4i.
Errori comuni
Un errore comune commesso dagli scolari che non hanno ancora capito quali siano gli zeri di una funzione è sostituire l'argomento (x) con zero e non il valore (y) della funzione. Sostituiscono con sicurezza x = 0 nell'equazione e, sulla base di ciò, trovano y. Ma questo è l'approccio sbagliato.
Un altro errore, come già accennato, è la riduzione per seno o coseno nell'equazione trigonometrica, motivo per cui si perdono uno o più zeri della funzione. Ciò non significa che nulla può essere ridotto in tali equazioni, ma questi fattori "persi" devono essere presi in considerazione in ulteriori calcoli.
Rappresentazione grafica
Puoi capire cosa sono gli zeri di una funzione con l'aiuto di programmi matematici come Maple. In esso, puoi costruire un grafico specificando il numero di punti desiderato e la scala desiderata. Quei punti in cui il grafico incrocia l'asse OX sono gli zeri desiderati. Questo è uno dei modi più veloci per trovare le radici di un polinomio, specialmente se il suo ordine è maggiore del terzo. Quindi se è necessario eseguire regolarmente calcoli matematici, trovare le radici di polinomi di gradi arbitrari, costruire grafici, Maple o un programma simile sarà semplicemente indispensabile per eseguire e verificare calcoli.
La rappresentazione matematica di una funzione mostra chiaramente come una quantità determini completamente il valore di un'altra quantità. Tradizionalmente si considerano funzioni numeriche che associano un numero a un altro. Lo zero di una funzione è solitamente chiamato il valore dell'argomento in corrispondenza del quale la funzione scompare.
Istruzione
1. Per trovare gli zeri di una funzione, è necessario equiparare il suo lato destro a zero e risolvere l'equazione risultante. Immagina di ricevere una funzione f(x)=x-5.
2. Per trovare gli zeri di questa funzione, prendiamo e uguagliamo il suo lato destro a zero: x-5=0.
3. Risolvendo questa equazione, otteniamo che x=5 e questo valore dell'argomento sarà lo zero della funzione. Cioè, quando il valore dell'argomento è 5, la funzione f(x) svanisce.
In sottomissione funzioni in matematica comprendere la relazione tra gli elementi degli insiemi. Per dirla più correttamente, si tratta di una “legge” secondo la quale a un intero elemento di un insieme (detto dominio di definizione) viene assegnato un certo elemento di un altro insieme (detto dominio dei valori).
Avrai bisogno
- Conoscenze di algebra e revisione matematica.
Istruzione
1. I valori funzioni questa è una certa area da cui la funzione può assumere valori. Diciamo la gamma funzioni f(x)=|x| da 0 a infinito. Scoprire significato funzioni a un certo punto, devi sostituire l'argomento funzioni il suo equivalente numerico, il numero risultante sarà significato m funzioni. Sia la funzione f(x)=|x| – 10 + 4x. scoprire significato funzioni nel punto x=-2. Sostituisci il numero -2 invece di x: f(-2)=|-2| – 10 + 4*(-2) = 2 – 10 – 8 = -16. Cioè significato funzioni al punto -2 è -16.
Nota!
Prima di cercare il valore di una funzione in un punto, assicurarsi che sia incluso nell'ambito della funzione.
Consigli utili
Con un metodo simile è possibile trovare il valore della funzione di più argomenti. La differenza è che invece di un numero, dovrai sostituirne diversi, in base al numero di argomenti della funzione.
La funzione è la relazione stabilita della variabile y dalla variabile x. Inoltre, l'intero valore di x, chiamato argomento, corrisponde al valore eccezionale di y - la funzione. In forma grafica, la funzione viene visualizzata su un sistema di coordinate cartesiane sotto forma di grafico. I punti di intersezione del grafico con l'asse delle ascisse, su cui sono tracciati gli argomenti x, sono detti zeri della funzione. Trovare zeri validi è uno dei compiti per trovare una data funzione. In questo caso vengono presi in considerazione tutti i valori ammissibili della variabile indipendente x, che costituiscono il dominio della definizione della funzione (OOF).
Istruzione
1. Lo zero della funzione è il valore dell'argomento x, in corrispondenza del quale il valore della funzione è zero. Tuttavia, solo quegli argomenti che sono inclusi nel dominio di definizione della funzione in studio possono essere zeri. Cioè, in così tanti valori per i quali la funzione f (x) ha un senso.
2. Annota la funzione data e uguagliala a zero, diciamo f(x) = 2x?+5x+2 = 0. Risolvi l'equazione risultante e trova le sue radici reali. Le radici dell'equazione quadratica vengono calcolate con il supporto della ricerca del discriminante. 2x? + 5x + 2 \u003d 0; D \u003d b? -4ac \u003d 5? -4 * 2 * 2 \u003d 9; x1 \u003d (-b +? D) / 2 * a \u003d (-5 + 3) / 2 * 2 \u003d -0,5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2 Quindi, in questo caso, due si ottengono le radici dell'equazione quadratica, corrispondenti agli argomenti della funzione iniziale f(x).
3. Controlla tutti i valori x rilevati per l'appartenenza al dominio di definizione della funzione data. Rileva OOF, per fare ciò, controlla l'espressione iniziale per la presenza di radici di grado pari della forma?f (x), per la presenza di frazioni in una funzione con un argomento al denominatore, per la presenza di logaritmico o espressioni trigonometriche.
4. Quando si considera una funzione con un'espressione sotto la radice di grado pari, prendi come dominio di definizione tutti gli argomenti x, i cui valori non trasformano l'espressione radice in un numero negativo (al contrario, la funzione lo fa non ha senso). Specificare se gli zeri rilevati della funzione rientrano in un determinato intervallo di valori x accettabili.
5. Il denominatore di una frazione non può svanire, quindi escludi quegli argomenti x che portano a tale risultato. Per le quantità logaritmiche, si dovrebbero considerare solo quei valori dell'argomento per i quali l'espressione stessa è maggiore di zero. Gli zeri di funzione che trasformano l'espressione sublogaritmica in zero o in un numero negativo devono essere eliminati dal risultato finale.
Nota!
Quando si trovano le radici di un'equazione, possono apparire radici extra. È facile verificarlo: è sufficiente sostituire nella funzione il valore ottenuto dell'argomento e assicurarsi che la funzione svanisca.
Consigli utili
A volte una funzione non è espressa esplicitamente attraverso il suo argomento, quindi è facile sapere qual è la funzione. Un esempio di questo è l'equazione di un cerchio.
Moduli per la televisione digitale
TV tricolore - aggiornamento software ricevitore
Ricevitore satellitare o ingresso TV satellitare ci interfaccia comune