Immagine dalla trasformata di Laplace originale. Le definizioni delle proprietà di base della trasformazione di Laplace sono la formula di Duhamel. Trasformata diretta di Laplace
Per risolvere lineare equazioni differenziali useremo la trasformata di Laplace.
Trasformata di Laplace chiama il rapporto
assegnazione di funzioni x (t) variabile reale T funzione di corrispondenza X(i) variabile complessa s (s = σ+ jω). in cui x (t) sono chiamati originale, X (s)- Immagine o immagine di Laplace e S- Variabile trasformata di Laplace. L'originale è indicato in minuscolo e la sua immagine è nella lettera maiuscola con lo stesso nome.
Si assume che la funzione X(T) soggetto alla trasformata di Laplace ha le seguenti proprietà:
1) funzione x (t)è definita e differenziabile a tratti sull'intervallo dove< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
8 Lezione 7 FUNZIONI OPERATORE DEI CIRCUITI Funzioni operatore e trasferimento Poli e zeri delle funzioni circuito 3 Conclusioni Funzioni operatore e trasferimento Una funzione operatore di una catena è una relazione
68 Lezione 7 PROCESSI DI TRANSIZIONE NEI CIRCUITI DEL PRIMO ORDINE Schema 1 Processi transitori nei circuiti RC del primo ordine 2 Processi transitori nei circuiti R del primo ordine 3 Esempi di calcolo dei processi transitori nei circuiti
4 CIRCUITI ELETTRICI LINEARI DI CORRENTE SINUSOIDALE AC E METODI DEL LORO CALCOLO 4.1 MACCHINE ELETTRICHE. PRINCIPIO DI GENERAZIONE DI CORRENTE SINUSOIDALE 4.1.012. La corrente sinusoidale è detta istantanea
Agenzia federale per l'istruzione Istituto statale di istruzione professionale superiore "KUBAN STATE UNIVERSITY" Facoltà di fisica e tecnologia Dipartimento di optoelettronica
~ ~ FKP Derivata della funzione di una variabile complessa FKP della Cauchy - Riemann condiziona il concetto di regolarità della FKP Immagine e forma di un numero complesso Forma della FKP: dove la funzione reale di due variabili è reale
Sezione II. Analisi matematica
E. Yu. Anokhina
LA STORIA DELLO SVILUPPO E LA FORMAZIONE DELLA TEORIA DELLA FUNZIONE DI UNA VARIABILE COMPLESSA (TFKP) DA PARTE DI UN SOGGETTO EDUCATIVO
Uno dei corsi di matematica difficili è il corso TFKP. La complessità di questo corso è dovuta, prima di tutto, alla varietà delle sue interrelazioni con altre discipline matematiche, storicamente espresse nell'ampia direzione applicata della scienza TFKP.
Nella letteratura scientifica sulla storia della matematica, ci sono informazioni sparse sulla storia dello sviluppo di TFKP, richiedono sistematizzazione e generalizzazione.
A questo proposito, il compito principale di questo articolo è descrivere brevemente lo sviluppo di TFKP e la formazione di questa teoria come materia accademica.
Come risultato dello studio, sono state identificate le seguenti tre fasi nello sviluppo di TFKP come materia scientifica e accademica:
Lo stadio di emergenza e riconoscimento dei numeri complessi;
Lo stadio di accumulazione del materiale fattuale secondo le funzioni dei valori immaginari;
Fase di formazione della teoria delle funzioni di una variabile complessa.
La prima tappa nello sviluppo del TFKP (metà XVI - XVIII secolo) inizia con l'opera di G. Cardano (1545) che pubblicò l'opera “Artis magnae sive de regulis algebraitis” (Grande arte, ovvero sulle regole algebriche) . Il lavoro di J. Cardano ebbe il compito principale di sostanziare metodi algebrici generali per la risoluzione di equazioni di terzo e quarto grado, non molto tempo prima di quello scoperto da Ferro (1465-1526), Tartaglia (1506-1559) e Ferrari (1522). -1565). Se l'equazione cubica è ridotta alla forma
x3 + px + q = 0,
e dovrebbe esserci
Quando (μ ^ Ap V (| - 70 l'equazione ha tre radici reali, due delle quali
sono uguali tra loro. Se quindi l'equazione ha un reale e due co-
radice complessa contorta. I numeri complessi compaiono nel risultato finale, quindi J. Cardano potrebbe aver fatto quello che ha fatto prima di lui: dichiarare l'equazione avere
una radice. Quando (<7 Г + (р V < (). тогда уравнение имеет три действительных корня. Этот так
il caso detto irriducibile è caratterizzato da una particolarità che non fu riscontrata fino al XVI secolo. L'equazione x3 - 21x + 20 = 0 ha tre radici reali 1, 4, - 5 che è facile
assicurarsi con una semplice sostituzione. Ma ^ du + y _ ^ 20 anni + ^ -21 anni _ ^ ^ ^; quindi, secondo la formula generale, x = ^ -10 + ^ -243 - ^ - 10-4 ^ 243. Complesso, cioè "Falso", il numero non è qui il risultato, ma un termine intermedio nei calcoli che portano alle radici reali dell'equazione in questione. J. Cardano ha affrontato una difficoltà e si è reso conto che per preservare la generalità di questa formula, è necessario abbandonare la completa ignoranza dei numeri complessi. J. D'Alembert (1717-1783) riteneva che fosse proprio questa circostanza a indurre J. Cardano ei matematici che seguirono questa idea ad interessarsi seriamente ai numeri complessi.
In questa fase (nel XVII secolo) erano generalmente accettati due punti di vista. Il primo punto di vista è stato espresso da Girard, che ha sollevato la questione del riconoscimento della necessità di un uso illimitato dei numeri complessi da parte di qualsiasi cosa. Il secondo era di Cartesio, che negava la possibilità di interpretare i numeri complessi. Opposto all'opinione di Cartesio era il punto di vista di J. Wallis: l'esistenza di una reale interpretazione dei numeri complessi è stata ignorata da Cartesio. I numeri complessi iniziarono ad essere "forzati" per essere utilizzati nella risoluzione di problemi applicati in situazioni in cui l'uso di numeri reali portava a un risultato complesso, o il risultato non poteva essere ottenuto teoricamente, ma aveva un'implementazione pratica.
L'uso intuitivo dei numeri complessi ha portato alla necessità di preservare le leggi e le regole dell'aritmetica dei numeri reali per un insieme di numeri complessi, in particolare, ci sono stati tentativi di trasferimento diretto. Questo a volte portava a risultati errati. A questo proposito, sono diventate di attualità le questioni sulla giustificazione dei numeri complessi e la costruzione di algoritmi per la loro aritmetica. Questo fu l'inizio di una nuova fase nello sviluppo di TFKP.
La seconda fase nello sviluppo del TFKP (inizio del XVIII secolo - XIX secolo). Nel XVIII sec. L. Eulero ha espresso l'idea della chiusura algebrica del campo dei numeri complessi. La chiusura algebrica del campo dei numeri complessi C ha portato i matematici alle seguenti conclusioni:
Che lo studio delle funzioni e l'analisi matematica in generale acquisiscano la propria completezza e completezza solo quando si considera il comportamento delle funzioni in un dominio complesso;
È necessario considerare i numeri complessi come variabili.
Nel 1748 L. Euler (1707-1783) nella sua opera "Introduzione all'analisi degli infinitesimi" introdusse una variabile complessa come il concetto più generale di variabile, utilizzando i numeri complessi nell'espansione delle funzioni in fattori lineari. L. Euler è giustamente considerato uno dei creatori del TFKP. Nelle opere di L. Euler, sono state studiate in dettaglio le funzioni elementari di una variabile complessa (1740-1749), sono state fornite le condizioni per la differenziabilità (1755) e l'inizio del calcolo integrale delle funzioni di una variabile complessa (1777). L. Euler introdusse praticamente la mappatura conforme (1777). Chiamò queste mappature "simili in piccolo" e il termine "conforme" fu usato per la prima volta, a quanto pare, dall'accademico di San Pietroburgo F. Schubert (1789). L. Eulero guidò anche numerose applicazioni di funzioni di una variabile complessa a vari problemi matematici e pose le basi per la loro applicazione in idrodinamica (17551757) e cartografia (1777). K. Gauss formula la definizione di integrale nel piano complesso, un teorema integrale sullo sviluppo di una funzione analitica in una serie di potenze. Laplace utilizza variabili complesse per calcolare integrali difficili e sviluppa un metodo per risolvere equazioni lineari, alle differenze e differenziali noto come trasformata di Laplace.
Dal 1799 sono apparse opere in cui vengono date interpretazioni più o meno convenienti di un numero complesso e vengono definite azioni su di esse. Un'interpretazione teorica abbastanza generale e un'interpretazione geometrica furono pubblicate da K. Gauss solo nel 1831.
L. Euler e i suoi contemporanei hanno lasciato una ricca eredità ai discendenti sotto forma di fatti accumulati, da qualche parte sistemati, da qualche parte no, ma ancora sparsi sul TFKP. Possiamo dire che il materiale fattuale sulle funzioni delle quantità immaginarie, per così dire, ha richiesto la sua sistematizzazione sotto forma di una teoria. Questa teoria ha iniziato la sua formazione.
La terza fase della formazione del TFKP (XIX secolo - XX secolo). I principali risultati qui appartengono a O. Cauchy (1789-1857), B. Riemann (1826-1866) e K. Weierstrass (1815-1897). Ognuno di loro ha rappresentato una delle direzioni dello sviluppo del TFKP.
Il rappresentante della prima direzione, che nella storia della matematica era chiamata "la teoria delle funzioni monogeniche o differenziabili" era O. Cauchy. Ha formalizzato fatti sparsi sul calcolo differenziale e integrale delle funzioni di una variabile complessa, ha chiarito il significato dei concetti e delle operazioni di base con quelli immaginari. Nei lavori di O. Cauchy, si afferma la teoria dei limiti e la teoria delle serie e delle funzioni elementari basate su di essa, viene formulato un teorema che chiarisce completamente il dominio di convergenza di una serie di potenze. Nel 1826, O. Cauchy introdusse il termine: detrazione (letteralmente: resto). Nei suoi scritti dal 1826 al 1829 creò la teoria delle deduzioni. O. Cauchy ha derivato una formula integrale; ottenuto un teorema di esistenza per uno sviluppo di una funzione di una variabile complessa in serie di potenze (1831). O. Cauchy ha posto le basi per la teoria delle funzioni analitiche di più variabili; determinato i rami principali delle funzioni multivalore di una variabile complessa; primi tagli piani utilizzati (1831-1847). Nel 1850 introdusse il concetto di funzioni monodromiche, distinguendo la classe delle funzioni monogeniche.
Un seguace di O. Cauchy fu B. Riemann, che creò anche la sua (seconda) direzione "geometrica" dello sviluppo di TFKP. Nelle sue opere, ha superato l'isolamento delle idee sulle funzioni di variabili complesse e ha formato nuovi dipartimenti di questa teoria, strettamente correlati ad altre discipline. Riemann ha compiuto un nuovo significativo passo nella storia della teoria delle funzioni analitiche, proponendo di collegare la rappresentazione della mappatura di una regione all'altra con ciascuna funzione di una variabile complessa. Ha stabilito una distinzione tra le funzioni di un complesso e una variabile reale. B. Riemann ha posto le basi per la teoria geometrica delle funzioni, ha introdotto la superficie di Riemann, ha sviluppato la teoria delle mappature conformi, ha stabilito una connessione tra funzioni analitiche e armoniche e ha introdotto la funzione zeta in considerazione.
L'ulteriore sviluppo di TFKP ha avuto luogo in una diversa (terza) direzione. La base della quale era la possibilità di rappresentare le funzioni per serie di potenze. Il nome “analitico” è rimasto impresso nella storia per questa direzione. Si è formato nelle opere di K. Weierstrass, in cui ha portato alla ribalta il concetto di convergenza uniforme. K. Weierstrass ha formulato e dimostrato un teorema sulla legalità della riduzione di termini simili in una serie. K. Weierstrass ottenne un risultato fondamentale: il limite di una sequenza di funzioni analitiche convergenti uniformemente all'interno di un certo dominio è una funzione analitica. Seppe generalizzare il teorema di Cauchy sull'espansione in serie di potenze di una funzione di una variabile complessa e descrisse il processo di continuazione analitica delle serie di potenze e la sua applicazione alla rappresentazione delle soluzioni di un sistema di equazioni differenziali. K. Weierstrass ha stabilito il fatto non solo della convergenza assoluta della serie, ma anche della convergenza uniforme. Appare il teorema di Weierstrass sull'espansione di un'intera funzione in un prodotto. Pone le basi per la teoria delle funzioni analitiche di più variabili, costruisce la teoria della divisibilità delle serie di potenze.
Considera lo sviluppo della teoria delle funzioni analitiche in Russia. Matematici russi del XIX secolo. per molto tempo non hanno voluto dedicarsi a un nuovo campo della matematica. Nonostante ciò, si possono nominare diversi nomi per i quali non era estranea ed elencare alcune delle opere e dei risultati di questi matematici russi.
Uno dei matematici russi era M.V. Ostrogradskij (1801-1861). Sulla ricerca di M.V. Poco si sa di Ostrogradskii nel campo della teoria delle funzioni analitiche, ma O. Cauchy ha parlato con lodi di questo giovane scienziato russo, che ha applicato gli integrali e ha dato nuove prove di formule e ha generalizzato altre formule. M.V. Ostrogradskiy ha scritto un articolo "Osservazioni sugli integrali definiti", in cui ha derivato la formula di Cauchy per il residuo di una funzione rispetto al polo di ordine n-esimo. Ha delineato l'applicazione della teoria dei residui e della formula di Cauchy al calcolo degli integrali definiti in un ampio corso di conferenze pubbliche tenuto nel 1858-1859.
Alcune opere di N.I. Lobachevsky, che sono di diretta importanza per la teoria delle funzioni di una variabile complessa. La teoria delle funzioni elementari di una variabile complessa è contenuta nella sua opera "Algebra o calcolo del finito" (Kazan, 1834). In cui cos x e sin x sono determinati inizialmente per x reale come reale e
la parte immaginaria della funzione ex ^. Utilizzando le proprietà precedentemente stabilite della funzione esponenziale e delle espansioni di potenza, vengono derivate tutte le proprietà principali delle funzioni trigonometriche. Di-
Apparentemente, Lobachevsky attribuiva particolare importanza a una tale costruzione puramente analitica della trigonometria, indipendente dalla geometria euclidea.
Si può affermare che negli ultimi decenni del XIX secolo. e il primo decennio del XX secolo. la ricerca fondamentale nella teoria delle funzioni di una variabile complessa (F. Klein, A. Poincaré, P. Kebe) è consistita nel graduale chiarimento del fatto che la geometria di Lobachevsky è allo stesso tempo la geometria delle funzioni analitiche di un complesso variabile.
Nel 1850, il professore dell'Università di San Pietroburgo (in seguito accademico) I.I. Somov (1815-1876) pubblicò I fondamenti della teoria delle funzioni analitiche, basati sui Nuovi fondamenti di Jacobi.
Tuttavia, il primo ricercatore russo veramente "originale" nel campo della teoria delle funzioni analitiche di una variabile complessa fu Yu.V. Sokhotsky (1842-1929). Ha difeso la sua tesi di laurea "La teoria dei residui integrali con alcune applicazioni" (San Pietroburgo, 1868). Dall'autunno del 1868, Yu.V. Sokhotsky tenne corsi sulla teoria delle funzioni di una variabile immaginaria e sulle frazioni continue con applicazioni all'analisi. Tesi di laurea Yu.V. Sokhotskii è dedicato alle applicazioni della teoria dei residui all'inversione di una serie di potenze (serie di Lagrange) e, in particolare, allo sviluppo di funzioni analitiche in frazioni continue, nonché ai polinomi di Legendre. In questo lavoro viene formulato e dimostrato il famoso teorema sul comportamento di una funzione analitica in un intorno di un punto essenzialmente singolare. La tesi di dottorato di Sokhotskiy
(1873) introdusse per la prima volta in forma espansa il concetto di integrale di tipo Cauchy: * y ^ & _ dove
aeb sono due numeri complessi arbitrari. Si assume che l'integrale sia preso lungo una curva ("traiettoria") che collega a e b. In questo lavoro vengono dimostrati alcuni teoremi.
Un ruolo enorme nella storia delle funzioni analitiche è stato svolto dalle opere di N.E. Zhukovsky e S.A. Chaplygin, che scoprì il campo sconfinato delle sue applicazioni in aerodinamica e idromeccanica.
Parlando dello sviluppo della teoria delle funzioni analitiche, non si possono non citare gli studi di S.V. Kovalevskaya, sebbene il loro significato principale sia al di fuori dei confini di questa teoria. Il successo del suo lavoro fu dovuto ad una formulazione completamente nuova del problema in termini di teoria delle funzioni analitiche e alla considerazione del tempo t come variabile complessa.
A cavallo del XX secolo. la natura della ricerca scientifica nel campo della teoria delle funzioni di una variabile complessa sta cambiando. Se prima la maggior parte della ricerca in quest'area veniva svolta in termini di sviluppo di una delle tre direzioni (la teoria delle funzioni di Cauchy monogeniche o differenziabili, le idee geometriche e fisiche di Riemann, la direzione analitica di Weierstrass), ora le differenze e le relative controversie sono in via di superamento, c'è e sta crescendo rapidamente il numero di opere in cui si realizza la sintesi di idee e metodi. Uno dei concetti fondamentali su cui si è palesata la connessione e la corrispondenza delle rappresentazioni geometriche e dell'apparato delle serie di potenze era il concetto di continuazione analitica.
Alla fine del XIX secolo. la teoria delle funzioni di una variabile complessa comprende un'ampia gamma di discipline: teoria geometrica delle funzioni basata sulla teoria delle mappature conformi e superfici di Riemann. Ha ricevuto una forma integrale della teoria dei vari tipi di funzioni: intere e meromorfe, ellittiche e modulari, automorfe, armoniche, algebriche. In stretta connessione con quest'ultima classe di funzioni, è stata sviluppata la teoria degli integrali abeliani. La teoria analitica delle equazioni differenziali e la teoria analitica dei numeri erano adiacenti a questo complesso. La teoria delle funzioni analitiche ha stabilito e rafforzato legami con altre discipline matematiche.
La ricchezza delle interrelazioni del TFKP con l'algebra, la geometria e altre scienze, la creazione dei fondamenti sistematici della scienza del TFKP stesso, il suo grande significato pratico hanno contribuito alla formazione del TFKP come materia accademica. Tuttavia, contemporaneamente al completamento della formazione delle basi, sono state introdotte nuove idee nella teoria delle funzioni analitiche, modificandone significativamente la composizione, la natura e gli obiettivi. Appaiono monografie che contengono una presentazione sistematica della teoria delle funzioni analitiche in uno stile vicino all'assiomatico e hanno anche obiettivi educativi. Apparentemente, l'importanza dei risultati su TFKP, ottenuti dagli scienziati del periodo in esame, li ha spinti a divulgare TFKP sotto forma di conferenze e pubblicazione di studi monografici in una prospettiva didattica. Possiamo concludere sull'emergere di TFKP come strumento educativo
materia. Nel 1856 C. Briot e T. Bouquet pubblicarono un breve libro di memorie "Indagine sulle funzioni di una variabile immaginaria", che è essenzialmente il primo libro di testo. I concetti generali della teoria delle funzioni di una variabile complessa iniziarono a essere sviluppati durante le lezioni. Dal 1856 K. Weierht-rass ha tenuto conferenze sulla rappresentazione delle funzioni per serie di potenze convergenti e dal 1861 - sulla teoria generale delle funzioni. Nel 1876 apparve un'opera speciale di K. Weierstrass: "Sulla teoria delle funzioni analitiche a valore singolo", e nel 1880 "Sulla dottrina delle funzioni", in cui la sua teoria delle funzioni analitiche acquisì una certa completezza.
Le lezioni di Weierstrass sono servite per molti anni come prototipo di libri di testo sulla teoria delle funzioni di una variabile complessa, che da allora hanno cominciato ad apparire abbastanza spesso. Fu nelle sue lezioni che fondamentalmente fu costruito il moderno standard di rigore nell'analisi matematica e fu messa in luce la struttura che è diventata tradizionale.
ELENCO BIBLIOGRAFICO
1. Andronov I.K. Matematica dei numeri reali e complessi. Mosca: Istruzione, 1975.
2. Klein F. Lezioni sullo sviluppo della matematica nel XIX secolo. M.: ONTI, 1937. Parte 1.
3. Lavrent'ev M.A., Shabat B.V. Metodi della teoria delle funzioni di una variabile complessa. Mosca: Nauka, 1987.
4. Markushevich A.I. Teoria delle funzioni analitiche. M.: Stato. casa editrice di letteratura tecnica e teorica, 1950.
5. Matematica del XIX secolo. Geometria. Teoria delle funzioni analitiche / ed. A.N. Kolmogorov e A.P. Yushkevich. Mosca: Nauka, 1981.
6. Enciclopedia della matematica / cap. ed. I. M. Vinogradov. Mosca: Enciclopedia Sovietica, 1977.Vol. 1.
7. Enciclopedia matematica / cap. ed. I. M. Vinogradov. Mosca: Enciclopedia Sovietica, 1979.Vol. 2.
8. Giovane V.N. Fondamenti della dottrina del numero nel XVIII e all'inizio del XIX secolo. M.: Uchpedgiz, 1963.
9. Rybnikov K.A. Storia della matematica. Mosca: Casa editrice dell'Università statale di Mosca, 1963. Parte 2.
NON. Lyakhova TOCCARE LE CURVE DEL PIANO
La questione della tangenza delle curve piane, nel caso in cui le ascisse dei punti comuni si trovino da un'equazione della forma Pn x = 0, dove P x è un polinomio, è direttamente correlata alla domanda
sulla molteplicità delle radici del polinomio Pn x. In questo articolo, vengono formulate le istruzioni corrispondenti per i casi di assegnazione esplicita e implicita di funzioni i cui grafici sono curve e viene mostrata l'applicazione di queste istruzioni nella risoluzione di problemi.
Se le curve che sono grafici delle funzioni y = f (x) e y = cp x hanno un punto comune
M() x0; v0, cioè y0 = f x0 = cp x0 e tangenti alle curve indicate tracciate nel punto M() x0; v0 non coincidono, quindi dicono che le curve y = fix) e y - cp x si intersecano nel punto Mo xo; Yo
La Figura 1 mostra un esempio di intersezione di grafici di funzioni.
Questo è il nome di un altro tipo di trasformata integrale, che, insieme alla trasformata di Fourier, è ampiamente utilizzata nell'ingegneria radio per risolvere un'ampia varietà di problemi relativi allo studio dei segnali.
Concetto di frequenza complessa.
I metodi spettrali, come è già noto, si basano sul fatto che il segnale in esame è rappresentato come somma di un numero infinitamente grande di termini elementari, ciascuno dei quali cambia periodicamente nel tempo secondo la legge.
La naturale generalizzazione di questo principio sta nel fatto che al posto di segnali esponenziali complessi con indicatori puramente immaginari, vengono introdotti segnali esponenziali della forma, dove è un numero complesso: chiamato frequenza complessa.
Due segnali così complessi possono essere utilizzati per comporre un segnale reale, ad esempio, secondo la seguente regola:
dove è il valore coniugato complesso.
Infatti, in questo caso
![]()
A seconda della scelta delle parti reale e immaginaria della frequenza complessa, si possono ottenere vari segnali reali. Quindi, if, ma ottieni le solite oscillazioni armoniche della forma If, allora, a seconda del segno, ottieni oscillazioni esponenziali crescenti o decrescenti nel tempo. Tali segnali acquisiscono una forma più complessa quando. Qui, il moltiplicatore descrive un inviluppo che cambia esponenzialmente nel tempo. Alcuni segnali tipici sono mostrati in fig. 2.10.
Il concetto di frequenza complessa risulta essere molto utile, innanzitutto, perché permette, senza ricorrere a funzioni generalizzate, di ottenere rappresentazioni spettrali di segnali i cui modelli matematici non sono integrabili.

Riso. 2.10. Segnali reali corrispondenti a diversi valori della frequenza complessa
Anche un'altra considerazione è essenziale: i segnali esponenziali della forma (2.53) servono come mezzo "naturale" per studiare le oscillazioni in vari sistemi lineari. Queste domande verranno approfondite nel cap. otto.
Va notato che la vera frequenza fisica è la parte immaginaria della frequenza complessa. Non esiste un termine speciale per la parte reale della frequenza complessa.
Relazioni di base.
Sia un segnale, reale o complesso, definito a t> 0 e uguale a zero a valori di tempo negativi. La trasformata di Laplace di questo segnale è funzione di una variabile complessa data da un integrale:

Il segnale è chiamato l'originale e la funzione è chiamata la sua immagine di Laplace (in breve, solo l'immagine).
La condizione che garantisce l'esistenza dell'integrale (2.54) è la seguente: il segnale deve avere un tasso di crescita non superiore all'esponenziale, cioè deve soddisfare la disuguaglianza dove sono numeri positivi.
Quando tale disuguaglianza è soddisfatta, la funzione esiste nel senso che l'integrale (2.54) converge assolutamente per tutti i numeri complessi per i quali il Numero a è detto ascissa di convergenza assoluta.
La variabile nella formula principale (2.54) è identificabile con la frequenza complessa Infatti, ad una frequenza complessa puramente immaginaria, quando la formula (2.54) si trasforma nella formula (2.16), che determina la trasformata di Fourier del segnale, che è zero a Quindi, la trasformata di Laplace può essere considerata
Proprio come avviene nella teoria della trasformata di Fourier, è possibile, conoscendo l'immagine, ripristinare l'originale. Per questo, nella formula inversa della trasformata di Fourier

si dovrebbe effettuare una continuazione analitica, passando dalla variabile immaginaria all'argomento complesso a. Sul piano della frequenza complessa, l'integrazione si effettua lungo un asse verticale infinitamente lungo posto a destra dell'ascissa di convergenza assoluta. Poiché at è il differenziale, la formula per la trasformata di Laplace inversa assume la forma

Nella teoria delle funzioni di una variabile complessa, è dimostrato che le immagini di Laplace hanno proprietà "buone" dal punto di vista della levigatezza: tali immagini in tutti i punti del piano complesso, ad eccezione di un insieme numerabile di cosiddetti punti singolari, sono funzioni analitiche. I punti singolari, di regola, sono poli, singoli o multipli. Pertanto, per calcolare integrali della forma (2.55), si possono utilizzare metodi flessibili della teoria dei residui.
In pratica sono molto utilizzate le trasformate di Laplace, che raccolgono informazioni sulla corrispondenza tra gli originali. e immagini. La presenza di tabelle ha reso popolare il metodo della trasformata di Laplace sia negli studi teorici che nei calcoli ingegneristici di dispositivi e sistemi di ingegneria radio. Nelle Appendici c'è una tale tabella che consente di risolvere una gamma abbastanza ampia di problemi.
Esempi di calcolo delle trasformate di Laplace.
I metodi di calcolo delle immagini hanno molto in comune con quanto già studiato in relazione alla trasformata di Fourier. Consideriamo i casi più tipici.
Esempio 2.4, Immagine del momento esponenziale generalizzato.
Let, dove è un numero complesso fisso. La presenza della funzione - determina l'uguaglianza in Usando la formula (2.54), abbiamo

Se poi il numeratore scompare quando viene sostituito il limite superiore. Di conseguenza, otteniamo la corrispondenza
![]()
Come caso speciale della formula (2.56), puoi trovare l'immagine di un vero impulso video esponenziale:
![]()
e un segnale esponenziale complesso:
![]()
Infine, inserendo (2.57), troviamo l'immagine della funzione di Heaviside:
Esempio 2.5. Immagine della funzione delta.
Trasformata di Laplace- trasformazione integrale che lega la funzione F (s) (\ stile di visualizzazione \ F (s)) variabile complessa ( Immagine) con la funzione f (x) (\ stile di visualizzazione \ f (x)) variabile reale ( originale). Con il suo aiuto, vengono studiate le proprietà dei sistemi dinamici e vengono risolte le equazioni differenziali e integrali.
Una delle caratteristiche della trasformata di Laplace, che ha predeterminato il suo uso diffuso nei calcoli scientifici e ingegneristici, è che molti rapporti e operazioni sugli originali corrispondono a rapporti più semplici sulle loro immagini. Così, la convoluzione di due funzioni è ridotta nello spazio dell'immagine all'operazione di moltiplicazione e le equazioni differenziali lineari diventano algebriche.
YouTube collegiale
1 / 5
✪ Trasformata di Laplace - bezbotvy
Lezione 10: Trasformata di Laplace
✪ Matematica superiore - 4. Trasformate di Laplace. Parte 1
Metodo di Laplace per la risoluzione di equazioni differenziali
✪ Lezione 11: Applicazione della trasformata di Laplace alla risoluzione di equazioni differenziali
Sottotitoli
Definizione
Trasformata diretta di Laplace
lim b → ∞ ∫ 0 b | f (x) | e - σ 0 x d x = ∫ 0 ∞ | f (x) | e - σ 0 xdx, (\ displaystyle \ lim _ (b \ to \ infty) \ int \ limit _ (0) ^ (b) | f (x) | e ^ (- \ sigma _ (0) x) \ , dx = \ int \ limit _ (0) ^ (\ infty) | f (x) | e ^ (- \ sigma _ (0) x) \, dx,)allora converge in modo assoluto e uniforme per ed è una funzione analitica per σ ⩾ σ 0 (\ displaystyle \ sigma \ geqslant \ sigma _ (0)) (σ = R e s (\ displaystyle \ sigma = \ mathrm (Re) \, s)- parte reale di una variabile complessa s (\ stile di visualizzazione s)). Bordo inferiore preciso σ a (\ stile di visualizzazione \ sigma _ (a)) serie di numeri (\ stile di visualizzazione \ sigma), in cui questa condizione è soddisfatta, si chiama ascissa di convergenza assoluta Trasformata di Laplace per la funzione.
- Condizioni per l'esistenza della trasformata diretta di Laplace
Trasformata di Laplace L (f (x)) (\ stile di visualizzazione (\ matematica (L)) \ (f (x) \)) esiste nel senso di convergenza assoluta nei seguenti casi:
- σ ⩾ 0 (\ displaystyle \ sigma \ geqslant 0): la trasformata di Laplace esiste se esiste un integrale 0 ∞ | f (x) | d x (\ displaystyle \ int \limits _ (0) ^ (\ infty) | f (x) | \, dx);
- > σ a (\ displaystyle \ sigma> \ sigma _ (a)): la trasformata di Laplace esiste se l'integrale 0 x 1 | f (x) | d x (\ displaystyle \ int \limits _ (0) ^ (x_ (1)) | f (x) | \, dx) esiste per ogni fine x 1> 0 (\ stile di visualizzazione x_ (1)> 0) e | f (x) | ⩽ K e σ a x (\ displaystyle | f (x) | \ leqslant Ke ^ (\ sigma _ (a) x)) per x> x 2 ⩾ 0 (\ displaystyle x> x_ (2) \ geqslant 0);
- σ> 0 (\ stile di visualizzazione \ sigma> 0) o > σ a (\ displaystyle \ sigma> \ sigma _ (a))(quale dei limiti è maggiore): la trasformata di Laplace esiste se esiste una trasformata di Laplace per la funzione f ′ (x) (\ stile di visualizzazione f "(x))(derivato da f (x) (\ stile di visualizzazione f (x))) per > σ a (\ displaystyle \ sigma> \ sigma _ (a)).
Nota
- Condizioni per l'esistenza della trasformata di Laplace inversa
Per l'esistenza della trasformata di Laplace inversa, è sufficiente soddisfare le seguenti condizioni:
- Se l'immagine F (s) (\ stile di visualizzazione F (s))- funzione analitica per σ ⩾ σ a (\ displaystyle \ sigma \ geqslant \ sigma _ (a)) e ha ordine minore di -1, quindi la trasformazione inversa esiste ed è continua per tutti i valori dell'argomento, e L - 1 (F (s)) = 0 (\ displaystyle (\ mathcal (L)) ^ (- 1) \ (F (s) \) = 0) per t ⩽ 0 (\ stile di visualizzazione t \ leqslant 0).
- Permettere F (s) = φ [F 1 (s), F 2 (s),…, F n (s)] (\ stile di visualizzazione F (s) = \ varphi), così φ (z 1, z 2,…, z n) (\ displaystyle \ varphi (z_ (1), \; z_ (2), \; \ ldots, \; z_ (n))) analitico su ciascuno z k (\ stile di visualizzazione z_ (k)) ed è uguale a zero per z 1 = z 2 =… = z n = 0 (\ stile di visualizzazione z_ (1) = z_ (2) = \ ldots = z_ (n) = 0), e F k (s) = L (fk (x)) (σ> σ ak: k = 1, 2,…, n) (\ stile di visualizzazione F_ (k) (s) = (\ mathcal (L)) \ (f_ (k) (x) \) \; \; (\ sigma> \ sigma _ (ak) \ due punti k = 1, \; 2, \; \ ldots, \; n)), allora esiste la trasformazione inversa e la corrispondente trasformazione diretta ha l'ascissa di convergenza assoluta.
Nota: queste sono condizioni sufficienti per l'esistenza.
- teorema di convoluzione
Articolo principale: teorema di convoluzione
- Differenziare e integrare l'originale
L'immagine di Laplace della prima derivata dell'originale rispetto all'argomento è il prodotto dell'immagine per l'argomento di quest'ultimo meno l'originale a zero a destra:
L (f ′ (x)) = s ⋅ F (s) - f (0 +). (\ displaystyle (\ mathcal (L)) \ (f "(x) \) = s \ cdot F (s) -f (0 ^ (+)).)Teoremi del valore iniziale e finale (teoremi limite):
f (∞) = lim s → 0 s F (s) (\ stile di visualizzazione f (\ infty) = \ lim _ (s \ a 0) sF (s)) se tutti i poli della funzione s F (s) (\ stile di visualizzazione sF (s)) sono nel semipiano sinistro.Il teorema del valore finito è molto utile perché descrive il comportamento dell'originale all'infinito utilizzando una semplice relazione. Questo è, ad esempio, utilizzato per analizzare la stabilità della traiettoria di un sistema dinamico.
- Altre proprietà
Linearità:
L (a f (x) + b g (x)) = a F (s) + b G (s). (\ stile di visualizzazione (\ matematica (L)) \ (af (x) + bg (x) \) = aF (s) + bG (s).)Moltiplicazione per un numero:
L (f (a x)) = 1 a F (s a). (\ displaystyle (\ mathcal (L)) \ (f (ax) \) = (\ frac (1) (a)) F \ left ((\ frac (s) (a)) \ right).)Trasformata di Laplace diretta e inversa di alcune funzioni
Di seguito è riportata una tabella della trasformata di Laplace per alcune funzioni.
| № | Funzione | Dominio del tempo x (t) = L - 1 (X (s)) (\ stile di visualizzazione x (t) = (\ mathcal (L)) ^ (- 1) \ (X (s) \)) |
Dominio della frequenza X (s) = L (x (t)) (\ stile di visualizzazione X (s) = (\ mathcal (L)) \ (x (t) \)) |
Regione di convergenza per sistemi causali |
|---|---|---|---|---|
| 1 | ritardo perfetto | δ (t - τ) (\ stile di visualizzazione \ delta (t- \ tau) \) | e - τ s (\ stile di visualizzazione e ^ (- \ tau s) \) | |
| 1a | singolo impulso | δ (t) (\ stile di visualizzazione \ delta (t) \) | 1 (\ stile di visualizzazione 1 \) | ∀ s (\ stile di visualizzazione \ per tutti i s \) |
| 2 | ritardo n (\ stile di visualizzazione n) | (t - τ) n n! e - α (t - τ) ⋅ H (t - τ) (\ stile di visualizzazione (\ frac ((t- \ tau) ^ (n)) (n}e^{-\alpha (t-\tau)}\cdot H(t-\tau)} !} | e - τ s (s + α) n + 1 (\ displaystyle (\ frac (e ^ (- \ tau s)) ((s + \ alpha) ^ (n + 1))))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2a | sedare n (\ stile di visualizzazione n)-esimo ordine | t n n! ⋅ H (t) (\ stile di visualizzazione (\ frac (t ^ (n)) (n}\cdot H(t)} !} | 1 s n + 1 (\ stile di visualizzazione (\ frac (1) (s ^ (n + 1)))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2a.1 | sedare q (\ stile di visualizzazione q)-esimo ordine | t q Γ (q + 1) ⋅ H (t) (\ stile di visualizzazione (\ frac (t ^ (q)) (\ Gamma (q + 1))) \ cdot H (t)) | 1 s q + 1 (\ stile di visualizzazione (\ frac (1) (s ^ (q + 1)))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2a.2 | funzione dell'unità | H (t) (\ stile di visualizzazione H (t) \) | 1 s (\ stile di visualizzazione (\ frac (1) (s))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2b | funzione unità di ritardo | H (t - τ) (\ stile di visualizzazione H (t- \ tau) \) | e - τ s s (\ stile di visualizzazione (\ frac (e ^ (- \ tau s)) (s))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2c | Passo di velocità | t ⋅ H (t) (\ stile di visualizzazione t \ cdot H (t) \) | 1 s 2 (\ stile di visualizzazione (\ frac (1) (s ^ (2)))) | s> 0 (\ stile di visualizzazione s> 0) |
| 2d | n (\ stile di visualizzazione n)-esimo ordine con spostamento di frequenza | t n n! e - α t ⋅ H (t) (\ stile di visualizzazione (\ frac (t ^ (n)) (n}e^{-\alpha t}\cdot H(t)} !} | 1 (s + α) n + 1 (\ stile di visualizzazione (\ frac (1) ((s + \ alpha) ^ (n + 1))))) | s> - α (\ stile di visualizzazione s> - \ alpha) |
| 2d.1 | decadimento esponenziale | e - α t ⋅ H (t) (\ stile di visualizzazione e ^ (- \ alpha t) \ cdot H (t) \) | 1 s + α (\ stile di visualizzazione (\ frac (1) (s + \ alpha))) | s> - α (\ stile di visualizzazione s> - \ alpha \) |
| 3 | approssimazione esponenziale | (1 - e - α t) ⋅ H (t) (\ stile di visualizzazione (1-e ^ (- \ alpha t)) \ cdot H (t) \) | α s (s + α) (\ stile di visualizzazione (\ frac (\ alpha) (s (s + \ alpha)))) | s> 0 (\ stile di visualizzazione s> 0 \) |
| 4 | seno | sin (ω t) ⋅ H (t) (\ displaystyle \ sin (\ omega t) \ cdot H (t) \) | ω s 2 + ω 2 (\ stile di visualizzazione (\ frac (\ omega) (s ^ (2) + \ omega ^ (2)))) | s> 0 (\ stile di visualizzazione s> 0 \) |
| 5 | coseno | cos (ω t) ⋅ H (t) (\ stile di visualizzazione \ cos (\ omega t) \ cdot H (t) \) | s s 2 + ω 2 (\ stile di visualizzazione (\ frac (s) (s ^ (2) + \ omega ^ (2)))) | s> 0 (\ stile di visualizzazione s> 0 \) |
| 6 | seno iperbolico | s h (α t) ⋅ H (t) (\ displaystyle \ mathrm (sh) \, (\ alpha t) \ cdot H (t) \) | α s 2 - α 2 (\ stile di visualizzazione (\ frac (\ alpha) (s ^ (2) - \ alpha ^ (2)))) | s> | α | (\ stile di visualizzazione s> | \ alfa | \) |
| 7 | coseno iperbolico | c h (α t) ⋅ H (t) (\ displaystyle \ mathrm (ch) \, (\ alpha t) \ cdot H (t) \) | s s 2 - α 2 (\ stile di visualizzazione (\ frac (s) (s ^ (2) - \ alpha ^ (2)))) | s> | α | (\ stile di visualizzazione s> | \ alfa | \) |
| 8 | decadimento esponenziale seno |
e - α t sin (ω t) ⋅ H (t) (\ displaystyle e ^ (- \ alpha t) \ sin (\ omega t) \ cdot H (t) \) | ω (s + α) 2 + ω 2 (\ stile di visualizzazione (\ frac (\ omega) ((s + \ alpha) ^ (2) + \ omega ^ (2)))) | s> - α (\ stile di visualizzazione s> - \ alpha \) |
| 9 | decadimento esponenziale coseno |
e - α t cos (ω t) ⋅ H (t) (\ displaystyle e ^ (- \ alpha t) \ cos (\ omega t) \ cdot H (t) \) | s + α (s + α) 2 + ω 2 (\ stile di visualizzazione (\ frac (s + \ alpha) ((s + \ alpha) ^ (2) + \ omega ^ (2)))) | s> - α (\ stile di visualizzazione s> - \ alpha \) |
| 10 | radice n (\ stile di visualizzazione n)-esimo ordine | t n ⋅ H (t) (\ displaystyle (\ sqrt [(n)] (t)) \ cdot H (t)) | s - (n + 1) / n ⋅ Γ (1 + 1 n) (\ stile di visualizzazione s ^ (- (n + 1) / n) \ cdot \ Gamma \ left (1 + (\ frac (1) (n) ) \ Giusto)) | s> 0 (\ stile di visualizzazione s> 0) |
| 11 | logaritmo naturale | ln (t t 0) ⋅ H (t) (\ displaystyle \ ln \ left ((\ frac (t) (t_ (0))) \ right) \ cdot H (t)) | - t 0 s [ln (t 0 s) + γ] (\ stile di visualizzazione - (\ frac (t_ (0)) (s)) [\ ln (t_ (0) s) + \ gamma]) | s> 0 (\ stile di visualizzazione s> 0) |
| 12 | Funzione Bessel primo tipo ordine n (\ stile di visualizzazione n) |
J n (ω t) ⋅ H (t) (\ stile di visualizzazione J_ (n) (\ omega t) \ cdot H (t)) | ω n (s + s 2 + ω 2) - ns 2 + ω 2 (\ displaystyle (\ frac (\ omega ^ (n) \ left (s + (\ sqrt (s ^ (2) + \ omega ^ (2 ) )) \ destra) ^ (- n)) (\ sqrt (s ^ (2) + \ omega ^ (2))))) | s> 0 (\ stile di visualizzazione s> 0 \) (n> - 1) (\ stile di visualizzazione (n> -1) \) |
| 13 | primo tipo ordine n (\ stile di visualizzazione n) |
I n (ω t) ⋅ H (t) (\ stile di visualizzazione I_ (n) (\ omega t) \ cdot H (t)) | ω n (s + s 2 - ω 2) - ns 2 - ω 2 (\ displaystyle (\ frac (\ omega ^ (n) \ left (s + (\ sqrt (s ^ (2) - \ omega ^ (2 ) )) \ destra) ^ (- n)) (\ sqrt (s ^ (2) - \ omega ^ (2))))) | s> | | (\ displaystyle s> | \ omega | \) |
| 14 | Funzione Bessel secondo tipo ordine zero |
Y 0 (α t) ⋅ H (t) (\ stile di visualizzazione Y_ (0) (\ alfa t) \ cdot H (t) \) | - 2 arsh (s / α) π s 2 + α 2 (\ displaystyle - (\ frac (2 \ mathrm (arsh) (s / \ alpha)) (\ pi (\ sqrt (s ^ (2) + \ alpha) ^ (2)))))) | s> 0 (\ stile di visualizzazione s> 0 \) |
| 15 | funzione Bessel modificata secondo tipo, ordine zero |
K 0 (α t) ⋅ H (t) (\ stile di visualizzazione K_ (0) (\ alfa t) \ cdot H (t)) | ||
| 16 | funzione di errore | e r f (t) ⋅ H (t) (\ displaystyle \ mathrm (erf) (t) \ cdot H (t)) | e s 2/4 e r f c (s / 2) s (\ displaystyle (\ frac (e ^ (s ^ (2) / 4) \ mathrm (erfc) (s / 2)) (s))) | s> 0 (\ stile di visualizzazione s> 0) |
Note alla tabella:
| ||||
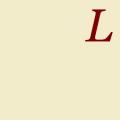 Linkedin: cos'è e come LinkedIn può aiutarti a trovare il lavoro dei tuoi sogni Rete professionale Linkedin
Linkedin: cos'è e come LinkedIn può aiutarti a trovare il lavoro dei tuoi sogni Rete professionale Linkedin Protezione DDoS: DDoS GUARD - il tuo hosting sicuro
Protezione DDoS: DDoS GUARD - il tuo hosting sicuro Gli smartphone Windows possono ora essere aggiornati utilizzando un PC
Gli smartphone Windows possono ora essere aggiornati utilizzando un PC