スケジュールに従った関数の零点。関数ゼロ。零点ルール

関数は最も重要な数学的概念の1つです。関数-変数の依存関係で変数からバツ、各値の場合バツ単一の値に一致しますで。変数バツ独立変数または引数と呼ばれます。変数で従属変数と呼ばれます。独立変数（変数バツ）関数の定義域を形成します。従属変数が取るすべての値（変数 y）、関数の範囲を形成します。

関数グラフそれらは、座標平面のすべての点のセットを呼び出します。その横軸は引数の値に等しく、縦軸は関数の対応する値、つまりの値に等しくなります。変数は横軸に沿ってプロットされますバツ、および変数の値はy軸に沿ってプロットされます y。関数をプロットするには、関数のプロパティを知る必要があります。関数の主なプロパティについては、以下で説明します。

関数グラフをプロットするには、プログラム-Graphing FunctionsOnlineを使用することをお勧めします。このページの資料を勉強しているときに質問がある場合は、いつでもフォーラムで質問できます。また、フォーラムでは、数学、化学、幾何学、確率論、および他の多くの主題の問題を解決するのに役立ちます！

関数の基本的なプロパティ。

1）機能範囲と機能範囲.

関数のスコープは、引数のすべての有効な値のセットですバツ（変数バツ）その機能 y = f（x）定義されています。
関数の範囲は、すべての実数値のセットです。 y関数が受け入れること。

初等数学では、関数は実数のセットでのみ研究されます。

2）関数の零点.

関数のゼロは、関数の値がゼロに等しくなる引数の値です。

3）関数の符号不変性の間隔.

関数定数符号間隔は、関数値が正または負のみである引数値のセットです。

4）関数の単調性.

増加関数（ある間隔で）-この間隔からの引数の値が大きいほど、関数の値が大きくなる関数。

減少関数（ある間隔で）-この間隔からの引数の値が大きいほど、関数の値が小さいことに対応する関数。

5）偶（奇）関数.

偶関数とは、定義域が原点および任意の関数に対して対称である関数です。バツ定義域からの平等 f（-x）= f（x）。偶関数のグラフは、y軸に対して対称です。

奇関数とは、定義域が原点および任意の関数に対して対称である関数です。バツ定義域からの平等 f（-x）= --f（x）。奇関数のグラフは、原点に関して対称です。

6）制限された無制限の機能.

| f（x）|のような正の数Mが存在する場合、関数は有界と呼ばれます。 xのすべての値に対して≤M。そのような数がない場合、関数は無制限です。

7）機能の周期性.

関数f（x）は、任意のx f（x + T）= f（x）のようにゼロ以外の数Tが存在する場合、周期的です。この最小数は、関数の期間と呼ばれます。すべての三角関数は周期的です。（三角関数の式）。

関数のこれらのプロパティを調べたら、関数を簡単に調べることができ、関数のプロパティを使用して、関数のグラフをプロットできます。また、真理値表、掛け算の九九、周期表、導関数の表、積分の表に関する資料も参照してください。

関数の零点

関数の零点とは何ですか？関数の零点を分析的およびグラフィカルに決定する方法は？

関数の零点関数がゼロに等しくなる引数の値です。

式y = f（x）で与えられる関数の零点を見つけるには、方程式f（x）= 0を解く必要があります。

方程式に根がない場合、関数には零点がありません。

1）線形関数y = 3x +15の零点を見つけます。

関数の零点を見つけるために、方程式3x + 15 = 0を解きます。

したがって、関数の零点はy = 3x + 15-x = -5です。

2）2次関数f（x）=x²-7x+ 12の零点を見つけます。

関数の零点を見つけるために、2次方程式を解きます

その根x1 = 3とx2 = 4はこの関数の零点です。

3）関数の零点を見つける

分母がゼロと異なる場合、分数は意味があります。したがって、x²-1≠0、x²≠1、x≠±1です。つまり、この関数の定義域（ODZ）

方程式x²+ 5x + 4 = 0 x1 = -1 x2 = -4の根から、x = -4のみが定義域に含まれます。

グラフィカルに与えられた関数の零点を見つけるには、関数のグラフとx軸との交点を見つける必要があります。

グラフがOx軸と交差しない場合、関数にはゼロがありません。

グラフが図に示されている関数には、4つのゼロがあります-

代数では、関数の零点を見つける問題は、独立したタスクとして、および他の問題を解決するとき、たとえば、関数を研究するとき、不等式を解くときなどに発生します。

www.algebraclass.ru

零点ルール

関数の基本的な概念とプロパティ

ルール（の法則）適合性。単調関数 .

制限付きおよび無制限の機能。継続的および

不連続関数 . 偶関数と奇関数。

周期関数。機能期間。

関数の零点 . 漸近線 .

関数の範囲と範囲。 初等数学では、関数は実数のセットでのみ研究されます R 。これは、関数の引数が、関数が定義されている実際の値のみをとることができることを意味します。また、実際の値のみを受け入れます。沢山のバツ引数のすべての有効な有効な値バツ、その機能 y = f (バツ）が定義され、 関数スコープ。沢山の Y すべての実数値 y関数が受け入れることは呼び出されます 機能範囲。これで、関数のより正確な定義を与えることができます。 ルール （法則）集合間の対応バツと Y , セットの各要素について バツセットから1つだけの要素を見つけることができます Y、関数と呼ばれます .

この定義から、次の場合に関数が与えられたと見なされます。

-関数のスコープが設定されますバツ ;

—関数値の範囲が設定されています Y ;

-対応の法の支配は既知であり、それぞれについて

引数値の場合、関数値は1つしか見つかりません。

関数の一意性に関するこの要件は必須です。

単調関数。 引数の任意の2つの値の場合バツ 1とバツ状態の2 バツ 2 > バツ 1が続く f (バツ 2) > f (バツ 1）、次に関数 f (バツ）と呼ばれる増加; もしあればバツ 1とバツ状態の2 バツ 2 > バツ 1が続く f (バツ 2)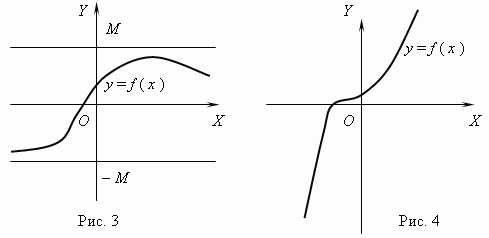

図3に示されている関数は有界ですが、単調ではありません。図4の関数は正反対で、単調ですが制限はありません。（これを説明してください！）

連続および不連続関数。 関数 y = f (バツ）と呼ばれる連続 その時点で バツ = a、もしも：

1）関数は次のように定義されていますバツ = a、つまり f (a）存在します。

2）存在する 有限の限界限界 f (バツ) ;

これらの条件の少なくとも1つが満たされない場合、関数が呼び出されます 不連続その時点でバツ = a .

関数が連続している場合 すべて その定義域のポイント、それからそれは呼ばれます 連続機能.

偶関数と奇関数。 の場合 どれか バツ関数定義のスコープから次のことが行われます。 f (— バツ) = f (バツ）、関数が呼び出されます平; もしそうなら： f (— バツ) = — f (バツ）、関数が呼び出されます奇数。偶関数のグラフ Y軸に対して対称（図5）、奇関数のグラフシム 原点に関するメトリック（図6）。

周期関数。 関数 f (バツ) — 定期刊行物そのようなものがあれば ゼロ以外番号 T何のために どれか バツ関数定義のスコープから次のことが行われます。 f (バツ + T) = f (バツ）。そのような 少しでも番号は呼ばれます 機能期間。すべての三角関数は周期的です。

例1。その罪を証明するバツ期間は2です。

解決策私たちはその罪を知っています（ x + 2 n）=罪バツ、どこ n= 0、±1、±2、…

したがって、2を追加します nサイン引数に

その値eを変更します。これで別の番号はありますか

ふりをしましょう P-そのような数、すなわち平等：

任意の値に有効バツ。しかし、それは

場所とでバツ= / 2、つまり

sin（/ 2 + P）= sin / 2 = 1。

しかし、還元公式によると、sin（/ 2 + P）= cos P。それで

これは、最後の2つの等式から得られます。 P= 1、しかし私たちは

これは次の場合にのみ当てはまります。 P = 2 n。最小から

2つのうちゼロ以外の数値 nが2の場合、この数

そして、期間の罪がありますバツ。同様に2

cosの期間ですバツ .

関数が日焼けしていることを証明するバツと猫バツ期間があります。

例2.sin2関数の周期はいくつですかバツ ?

解決策。罪2を考えてください。バツ= sin（2 x + 2 n）= sin [2（バツ + n) ] .

追加することがわかります n議論にバツ、変更されません

関数値。ゼロ以外の最小の数値

から nであるため、これは期間sin2です。バツ .

関数がnullです。 関数が0に等しい引数の値が呼び出されます ゼロ（ ルート）関数。関数は複数のゼロを持つことができます。たとえば、関数 y = バツ (バツ + 1) (バツ-3）3つのゼロがあります：バツ = 0, バツ = — 1, バツ= 3。幾何学的に 関数null – 関数のグラフと軸の交点の横軸です。 バツ .

図7は、ゼロのある関数のグラフを示しています。バツ = a , バツ = bとバツ = c .

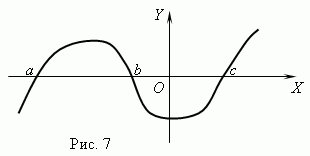
漸近線。 関数のグラフが原点から離れるにつれて無期限に特定の直線に近づく場合、この直線はと呼ばれます 漸近線.

トピック6.「間隔の方法」。

x x 0に対してf（x）f（x 0）の場合、関数f（x）が呼び出されます。 x0で連続.

関数がある区間Iのすべての点で連続である場合、それは呼び出されます 間隔で連続私（私が呼ばれる間隔 機能連続間隔). この間隔の関数のグラフは実線で、「紙から鉛筆を持ち上げずに描いた」と言われています。

連続関数のプロパティ。

区間（a; b）で関数fが連続で消えない場合、この区間で一定の符号を保持します。

1つの変数で不等式を解く方法は、このプロパティ（区間の方法）に基づいています。関数f（x）が区間Iで連続であり、この区間の有限数の点で消滅するとします。連続関数の特性により、これらの点はIを間隔に分割し、各間隔で連続関数f（x）cが一定の符号を保護します。この符号を決定するには、そのような各区間の任意の1点で関数f（x）の値を計算するだけで十分です。これに基づいて、区間法により不等式を解くための以下のアルゴリズムが得られます。

フォームの不等式の区間法

関数f（x）の定義域を見つけます;

関数f（x）の零点を見つけます;

定義域と関数の零点を数直線上に描きます。関数の零点は、その定義域を音程に分割します。各音程では、関数は一定の符号を保持します。

各区間の任意の1点で関数の値を計算することにより、取得した区間で関数の符号を見つけます。

答えを書き留めてください。

インターバル法。平均レベル。

あなたは自分の強さをテストし、統一国家試験またはOGEの準備ができているかどうかの結果を知りたいですか？

一次関数

この形式の関数は線形と呼ばれます。例として関数を取り上げましょう。 3″>で正、で負です。ポイントは関数（）の零点です。この関数の兆候を実際の軸に示しましょう。

「点を通過すると関数の符号が変わる」と言います。

関数の符号は、関数のグラフの位置に対応していることがわかります。グラフが軸の上にある場合、符号は「」であり、下にある場合は「」です。

結果のルールを任意の線形関数に一般化すると、次のアルゴリズムが得られます。

関数の零点を見つけます。

数値軸にマークを付けます。

ゼロの反対側で関数の符号を決定します。

二次関数

二次不等式がどのように解決されるかを覚えているといいのですが。そうでない場合は、トピック「正方形の不等式」をお読みください。二次関数の一般的な形式を思い出させてください。

ここで、2次関数が取る符号を思い出してみましょう。そのグラフは放物線であり、関数は、放物線が軸の上にある場合は記号「」を取り、放物線が軸の下にある場合は「」を取ります。

関数にゼロ（値）がある場合、放物線は2つの点（対応する2次方程式の根）で軸と交差します。このように、軸は3つの区間に分割され、各ルートを通過するときに関数の符号が交互に変化します。

毎回放物線を描かずに、どういうわけか標識を決定することは可能ですか？

二乗三項式は因数分解できることを思い出してください。

軸の根に注意してください：

関数の符号は、ルートを通過するときにのみ変更できることを覚えています。この事実を使用します。軸が根で分割される3つの区間のそれぞれについて、任意に選択された1つの点でのみ関数の符号を決定するだけで十分です。区間の他の点では、符号は同じ。

この例では、3″>の場合、括弧内の両方の式が正です（たとえば、0″>に置き換えます）。軸に記号「」を付けます。

ええと、（たとえば、代用して）両方の括弧が負の場合、積は正になります。

それはそれです インターバル法：各間隔の要因の兆候を知って、製品全体の兆候を決定します。

関数にゼロがない場合、または関数が1つしかない場合も考えてみましょう。

存在しない場合、ルートはありません。これは、「ルートを通過する」ことがないことを意味します。これは、数値軸全体の関数が1つの符号のみを取ることを意味します。関数に代入することで簡単に判別できます。

ルートが1つしかない場合、放物線は軸に接触するため、ルートを通過するときに関数の符号は変わりません。そのような状況のルールは何ですか？

このような関数を除外すると、2つの同じ要因が得られます。

そして、二乗された式はすべて負ではありません！したがって、関数の符号は変わりません。そのような場合、符号が変わらないルートを選択し、正方形で囲みます。

そのようなルートは呼ばれます多数.

不等式の間隔の方法

これで、放物線を描画せずに2次不等式を解くことができます。二次関数の符号を軸に配置し、不等式の符号に応じて間隔を選択するだけで十分です。例えば：

軸上の根を測定し、標識を配置します。

記号「」が付いた軸の部分が必要です。不等式は厳密ではないため、根自体もソリューションに含まれます。

ここで、有理不等式、つまり不等式について考えてみましょう。どちらの部分も有理式です（「有理方程式」を参照）。

例：

1つを除くすべての因子---ここでは「線形」です。つまり、1次のみに変数が含まれています。区間法を適用するには、このような線形因子が必要です。つまり、根を通過するときに符号が変化します。しかし、乗数にはまったくルーツがありません。これは、常に正である（自分で確認する）ため、不等式全体の兆候に影響を与えないことを意味します。これは、不等式の左側と右側を分割して、それを取り除くことができることを意味します。

これで、すべてが2次不等式の場合と同じになります。各要素が消えるポイントを決定し、軸上にこれらのポイントをマークして、記号を配置します。私はあなたの注意を非常に重要な事実に引き付けます：

偶数の場合は、前と同じように進みます。点を正方形で囲み、ルートを通過するときに符号を変更しません。ただし、奇数の場合、このルールは満たされません。ルートを通過するときに符号が変更されます。したがって、そのようなルートでは、それが私たちの倍数ではないかのように、追加で何もしません。上記の規則は、すべての偶数乗と奇数乗に適用されます。

答えには何を書きますか？

符号の交代に違反した場合は、非常に注意する必要があります。厳密でない不等式では、答えに次のように含める必要があるためです。 すべての塗りつぶされたポイント。しかし、それらのいくつかはしばしば独立しています、つまり、それらは影付きの領域に入りません。この場合、それらを孤立したドット（中括弧内）として応答に追加します。

例（自分で決める）：

回答：

要因の中でそれが単純である場合、これはルートです。これは、として表すことができるためです。
.

ここで、値はゼロになります。たとえば、次の式で与えられる関数の場合

nullであるため

関数の零点は、 関数の根.

関数の零点の概念は、対応する代数的構造の零元または零元を範囲に含むすべての関数について考慮することができます。

実変数の関数の場合、ゼロは関数のグラフがx軸と交差する値です。

関数の零点を見つけるには、多くの場合、数値法（たとえば、ニュートン法、勾配法）を使用する必要があります。

未解決の数学的問題の1つは、リーマンゼータ関数の零点を見つけることです。

多項式の根

も参照してください

文学

ウィキメディア財団。 2010。

他の辞書で「関数ゼロ」が何であるかを確認してください。

与えられた関数f（z）が消える点。したがって、N。f。 f（z）は、方程式f（z）= 0の根と同じです。たとえば、点0、π、π、2π、2π、...は、sinz関数の零点です。分析関数の零点（分析.....を参照）

零点、零点..。スペル辞書

この用語には他の意味があります。ゼロを参照してください。この記事の内容を記事「FunctionZero」に移動する必要があります。記事を統合することでプロジェクトを支援できます。マージの妥当性について話し合う必要がある場合は、これを置き換えてください...ウィキペディア

または、C文字列（C言語の名前から）またはASCIZ文字列（アセンブラdirective.ascizの名前から）は、プログラミング言語で文字列を表す方法であり、文字の配列を導入する代わりに使用されます。特殊な文字列タイプ、および終了... ... Wikipedia

場の量子論では、結合定数の繰り込み係数の消失の特性の受け入れられた（スラング）名前。ここで、g0は、相互作用ラグランジアン、物理学からの裸の結合定数です。相互作用によってドレスアップされた結合定数。平等Z..。物理百科事典

ヌル突然変異n-対立遺伝子-ヌル変異、n。対立遺伝子*ヌル突然変異、n。対立遺伝子*ヌル突然変異またはn。対立遺伝子またはサイレントa。それが起こったDNA配列の機能の完全な喪失につながる突然変異... 遺伝学。百科事典の辞書

一連の独立したランダムイベントまたは確率変数の任意のリモート要素によってのみ発生が決定される任意のイベント（いわゆる残差イベント）の確率論のステートメントは...... 数学的百科事典

1）任意の（実数または複素数）数を追加しても変化しないという特性を持つ数。記号0で示されます。任意の数のNによる積はNに等しくなります。2つの数の積がNに等しい場合、要因の1つ.. .. 数学的百科事典

後者に関して解決されていない独立変数間の関係によって与えられる関数。これらの関係は、関数を定義する方法の1つです。たとえば、関係x2 + y2 1 = 0はNを定義します。f。 … ソビエト大百科事典

引数値 z その下で f(z）と呼ばれるゼロになります。 ゼロ点、つまりもしも f(a）= 0、次に a-ゼロ点.

Def。ドット しかしと呼ばれる オーダーゼロn 、もしも FKPは次の形式で表すことができます f(z）=、ここで
分析関数と
0.

この場合、テイラー級数（43）の関数の展開では、最初の n 係数はゼロです

= =

等。のゼロの次数を決定します
および（1-cos z）で z = 0

=
=

ゼロ一次

1-cos z =
=

ゼロ2次

Def。ドット z =
と呼ばれる 無限遠点とゼロ関数 f(z）、もしも f(
）= 0。このような関数は、負の累乗の級数に展開されます。 z : f(z) =
。もしも最初 n 係数がゼロに等しい場合、次のようになります。 ゼロ次 n 無限遠点で： f(z) = z - n
.

孤立した特異点は次のように分けられます：a） 取り外し可能な特異点; b） オーダーポールn; の） 本質的な特異点.

ドット しかしと呼ばれる 取り外し可能な特異点関数 f(z）もしも z
a リム f(z) = から -有限数 .

ドット しかしと呼ばれる極n (n 1）機能 f(z）逆関数の場合
= 1/ f(z）次数がゼロ nその時点で しかし。このような関数は、常に次のように表すことができます。 f(z) =
、どこ
-分析関数と
.

ドット しかしと呼ばれる 重要なポイント関数 f(z）、もしも z
a リム f(z）存在しません。

ローラン級数

環状収束領域の場合を考えてみましょう r < | z 0 – a| < Rポイントを中心に しかし機能のために f(z）。 2つの新しいサークルを紹介します L 1 (r）と L 2 (R）ドットのあるリングの境界付近 zそれらの間の0。リングのセクションを作成し、セクションのエッジに沿って円を結合し、単連結領域に渡して、

コーシー積分公式（39）変数zに対して2つの積分を取得します

f(z 0) =
+
, (42)

統合は反対方向に進みます。

積分のために L 1条件| z 0 – a | > | z – a |、および積分について L 2リバースコンディション| z 0 – a | < | z – a |。したがって、係数1 /（ z – z 0）一連の展開（a）積分 L 2および直列（b）の積分 L一。その結果、分解が発生します f(z）の環状領域で ローラン級数正と負の累乗（ z 0 – a)

f(z 0) =
A n (z 0 – a) n (43)

どこ A n =
=
;A -n =

正の力の拡大 (z 0 - しかし）と呼ばれる 右の部分ローラン級数（テイラー級数）、負の数の展開と呼ばれます。 主要部分ローラン列。

サークル内の場合 L 1特異点はなく、関数は解析的です。（44）では、最初の積分はコーシーの定理によってゼロに等しく、正しい部分だけが関数の展開に残ります。展開の負の力（45）は、内側の円内で分析性に違反した場合にのみ表示され、孤立した特異点の近くの関数を説明するのに役立ちます。

ローラン級数（45）を構築するには f(z）一般式に従って展開係数を計算するか、に含まれる初等関数の展開を使用できます。 f(z).

用語数（ n）ローラン級数の主要部分のは、特異点のタイプによって異なります。 取り外し可能な特異点 (n = 0) ; 本質的な特異点 (n
); ポールn-次数(n - 終了番号）。

とのために f(z) = ドット z = 0 取り外し可能な特異点、なぜなら主要な部分はありません。 f(z) = (z -
) = 1 -

b） f(z) = ドット z = 0 - 一次ポール

f(z) = (z -
) = -

c） f(z) = e 1 / zドット z = 0 - 本質的な特異点

f(z) = e 1 / z =

もしも f(z）はドメインで分析的です Dを除いて m孤立した特異点および| z 1 | < |z 2 | < . . . < |z m| 、次に関数を累乗で拡張する場合 z平面全体がに分割されます m+1リング| z 私 | < | z | < | z 私+ 1 | ローラン級数はリングごとに異なる形をしています。権力を拡大するとき（ z – z 私）ローラン級数の収束領域は円です| z – z 私 | < r、どこ r 最も近い特異点までの距離です。

等。関数を展開する f(z) =ローラン級数の権力 zと（ z - 1).

解決。関数を次の形式で表します f(z) = - z 2 。等比数列の合計の式を使用します
。円の中| z |< 1 ряд сходится и f(z) = - z 2 (1 + z + z 2 + z 3 + z 4 + . . .) = - z 2 - z 3 - z 4-。。。、つまり分解には 正しい部。円の外側の領域に移動しましょう| z | > 1。関数を次の形式で表します
、ここで1 / | z| < 1, и получим разложение f(z) = z
=z + 1 +

なぜなら、パワーの関数の拡張（ z - 1）のように見える f(z) = (z - 1) -1 + 2 + (z - 1）みんなのために
1.

等。ローラン級数で機能を拡張 f(z) =
: a）度単位 zサークル内| z| < 1; b) по степеням z リング1< |z| < 3 ; c) по степеням (z – 2）。決定。関数を単純な分数に分解してみましょう
= =+=
. 条件から z =1
A = -1/2 , z =3
B = ½.

しかし） f(z) = ½ [
] = ½ [
-(1/3)
]、いつ| z|< 1.

b） f(z) = - ½ [
+
] = - (
）、1で< |z| < 3.

から） f(z) = ½ [
]= - ½ [
] =

= - ½ = -
、| 2-の場合 z| < 1

点を中心とした半径1の円です z = 2 .

場合によっては、べき級数を等比数列のセットに減らすことができ、その後、それらの収束の領域を簡単に決定できます。

等。級数の収束を調査します

. . . + + + + 1 + () + () 2 + () 3 + . . .

解決。これは、2つの等比数列の合計です。 q 1 = , q 2 =（）。それらの収束の条件から、それは次のようになります < 1 , < 1 или |z| > 1 , |z| < 2 , т.е. область сходимости ряда кольцо 1 < |z| < 2 .

関数の零点とは何ですか？答えは非常に単純です。これは数学用語であり、値がゼロである特定の関数の定義域を意味します。関数の零点は関数の零点とも呼ばれます関数の零点が何であるかを説明する最も簡単な方法は、いくつかの簡単な例を使用することです。

例

簡単な方程式y = x +3を考えてみましょう。関数の零点はyがゼロになった引数の値であるため、方程式の左辺に0を代入します。

この場合、-3が目的のゼロです。特定の関数に対して、方程式の根は1つだけですが、常にそうであるとは限りません。

別の例を考えてみましょう。

前の例のように、方程式の左側に0を代入します。

明らかに、この場合、関数にはx = 3とx = -3の2つの零点があります。方程式に3次の引数がある場合、3つのゼロがあります。多項式の根の数は、方程式の引数の最大次数に対応しているという簡単な結論を出すことができます。ただし、多くの関数、たとえばy = x 3は、一見するとこのステートメントと矛盾します。論理と常識は、この関数にはゼロが1つしかないことを示唆しています-点x = 0に。しかし、実際には3つのルーツがあり、それらはすべて一致しています。方程式を複雑な形で解くと、これが明らかになります。この場合、x = 0であり、その多重度は3です。前の例では、ゼロが一致しなかったため、多重度は1でした。

定義アルゴリズム

提示された例から、関数の零点を決定する方法は明らかです。アルゴリズムは常に同じです。

関数を記述します。
yまたはf（x）= 0に置き換えます。
結果の方程式を解きます。

最後の項目の複雑さは、方程式の引数の程度によって異なります。高度の方程式を解くときは、方程式の根の数が引数の最大累乗に等しいことを覚えておくことが特に重要です。これは、三角方程式の場合に特に当てはまります。三角方程式では、両方の部分を正弦または余弦で除算すると、根が失われます。

任意の次数方程式は、任意の多項式の零点を見つけるために特別に開発されたホーナー法によって最も簡単に解かれます。

関数の零点の値は、負と正の両方、実数、または複素平面にある、単一または複数の場合があります。または、方程式の根がない可能性があります。たとえば、関数y = 8は、この変数に依存しないため、どのxでもゼロにはなりません。

方程式y = x 2 -16には2つの根があり、両方とも複素平面にあります：x 1 = 4i、x 2 = -4i。

よくある間違い

関数の零点が何であるかをまだ実際に理解していない学童が犯すよくある間違いは、関数の値（y）ではなく、引数（x）をゼロに置き換えることです。彼らは自信を持って方程式にx = 0を代入し、これに基づいてyを見つけます。しかし、これは間違ったアプローチです。

すでに述べたように、もう1つのエラーは、三角方程式の正弦または余弦による減少です。これが、関数の1つ以上の零点が失われる理由です。これは、そのような方程式で何も減らすことができないという意味ではありませんが、これらの「失われた」要因は、さらなる計算で考慮に入れる必要があります。

グラフ表示

Mapleなどの数学プログラムを使用すると、関数の零点が何であるかを理解できます。その中で、希望するポイント数と希望するスケールを指定してグラフを作成できます。グラフがOX軸と交差するポイントは、目的のゼロです。これは、特にその次数が3番目よりも高い場合に、多項式の根を見つけるための最速の方法の1つです。したがって、定期的に数学計算を実行する必要がある場合は、任意の次数の多項式の根を見つけ、グラフを作成し、Mapleまたは同様のプログラムが計算の実行と検証に不可欠です。

関数の数学的表現は、ある量が別の量の値を完全に決定する方法を明確に示しています。従来、数値関数は、ある数値を別の数値に関連付けると見なされていました。関数の零点は通常、関数が消える引数の値と呼ばれます。

命令

1. 関数の零点を見つけるには、その右辺を零点に等しくして、結果の方程式を解く必要があります。関数f（x）= x-5が与えられていると想像してください。

2. この関数の零点を見つけるために、その右側をゼロと見なしてみましょう：x-5 = 0。

3. この方程式を解くと、x = 5が得られ、引数のこの値は関数の零点になります。つまり、引数の値が5の場合、関数f（x）は消えます。

提出中関数数学では、集合の要素間の関係を理解します。より正確に言えば、これは「法則」であり、あるセットの要素全体（定義のドメインと呼ばれる）に別のセットの特定の要素（値のドメインと呼ばれる）が割り当てられます。

必要になるだろう

代数と数学的レビューの知識。

命令

1. 値関数これは、関数が値を取得できる特定の領域です。範囲を言いましょう関数 f（x）= | x | 0から無限大まで。発見する意味関数ある時点で、引数を置き換える必要があります関数その数値的同等物、結果の数は次のようになります意味 m 関数。関数f（x）= | x |とします。 – 10 + 4x。発見する意味関数点x = -2で。 xの代わりに数値-2を代入します：f（-2）= | -2 | – 10 + 4 *（-2）= 2 – 10 – 8 = -16。つまり、意味関数ポイント-2では-16です。

ノート！
あるポイントで関数の値を探す前に、それが関数のスコープに含まれていることを確認してください。

役立つアドバイス
同様の方法で、いくつかの引数の関数の値を見つけることができます。違いは、関数の引数の数に応じて、1つの数値ではなく、複数の数値に置き換える必要があることです。

関数は、変数xからの変数yの確立された関係です。さらに、引数と呼ばれるxの値全体は、yの例外的な値（関数）に対応します。グラフ形式では、関数はグラフ形式でデカルト座標系に表示されます。引数xがプロットされている横軸とグラフの交点は、関数の零点と呼ばれます。有効な零点を見つけることは、特定の関数を見つけるタスクの1つです。この場合、関数定義（OOF）のドメインを形成する独立変数xのすべての許容値が考慮されます。

命令

1. 関数の零点は、関数の値がゼロになる引数xの値です。ただし、調査中の関数の定義域に含まれている引数のみをゼロにすることができます。つまり、関数f（x）が意味を持つような多くの値\ u200b \ u200bで。

2. 与えられた関数を書き留めて、それをゼロに等しくします。たとえば、f（x）= 2x？+ 5x + 2 = 0です。結果の方程式を解いて、その実数根を見つけます。二次方程式の根は、判別式を見つけることをサポートして計算されます。 2x？+ 5x + 2 \ u003d 0; D \ u003d b？-4ac \ u003d 5？-4 * 2 * 2 \ u003d 9; x1 \ u003d（-b +？d）/ 2 * a \ u003d（-5 + 3）/ 2 * 2 \ u003d -0.5; x2 \ u003d（-b-？d）/ 2 * a \ u003d（-5-3）/ 2 * 2 \ u003d-2。したがって、この場合、2つ初期関数f（x）の引数に対応する、2次方程式の根が取得されます。

3. 与えられた関数の定義域に属しているかどうか、検出されたすべてのx値を確認してください。 OOFを検出し、これを行うには、次の形式の根の存在について初期式をチェックしますか？f（x）、分母に引数を持つ関数の分数の存在、対数の存在、または三角関数の式。

4. 偶数次のルートの下に式がある関数を検討するときは、定義域ですべての引数xを取ります。その値は、ルート式を負の数に変換しません（逆に、関数は意味がありません）。関数の検出された零点が許容可能なx値の特定の範囲内にあるかどうかを指定します。

5. 分数の分母は消えることができないため、そのような結果につながる引数xを除外します。対数量の場合、式自体がゼロより大きい引数の値のみを考慮する必要があります。サブ対数式をゼロまたは負の数に変換する関数ゼロは、最終結果から破棄する必要があります。

ノート！
方程式の根を見つけるときに、余分な根が表示される場合があります。これを確認するのは簡単です。引数の取得値を関数に代入し、関数が消えることを確認するだけで十分です。

役立つアドバイス
関数が引数で明示的に表現されていない場合は、関数が何であるかを簡単に知ることができます。この例は、円の方程式です。

スケジュールに従った関数の零点。 関数ゼロ。 零点ルール