Переходные и импульсные характеристики rl цепи. Переходная характеристика. Импульсная характеристика. Импульсные характеристики электрических цепей. Министерство образования и науки Украины
Импульсная
(весовая) характеристика или импульсная
функция
цепи
–
это ее обобщенная характеристика,
являющаяся временной функцией, численно
равная реакции цепи на единичное
импульсное воздействие на ее входе при
нулевых начальных условиях (рис. 13.14);
другими словами, это отклик цепи,
свободной от начального запаса энергии
на дельта-функцию Дирана  на ее входе.
на ее входе.
|
|
Функцию  можно определить, рассчитав переходную
можно определить, рассчитав переходную
 или передаточную
или передаточную  функцию цепи.
функцию цепи.
Расчет функции  с использованием переходной функции
цепи. Пусть при входном воздействии
с использованием переходной функции
цепи. Пусть при входном воздействии  реакцией линейной электрической цепи
является
реакцией линейной электрической цепи
является  .
Тогда в силу линейности цепи при входном
воздействии, равном производной
.
Тогда в силу линейности цепи при входном
воздействии, равном производной  ,
реакция цепи будет равна производной
,
реакция цепи будет равна производной
 .
.
Как отмечалось,
при  ,
реакция цепи
,
реакция цепи  ,
а если
,
а если  ,
то реакция цепи будет
,
то реакция цепи будет  ,
т.е. импульсная функция
,
т.е. импульсная функция
Согласно свойству
выборки  произведение
произведение
 .
Таким образом, импульсная функция цепи
.
Таким образом, импульсная функция цепи
 .
(13.8)
.
(13.8)
Если  ,
то импульсная функция имеет вид
,
то импульсная функция имеет вид
 .
(13.9)
.
(13.9)
Следовательно, размерность импульсной характеристики равна размерности переходной характеристики, поделенной на время.
Расчет функции  с использованием передаточной функции
цепи. Согласно выражению (13.6), при
воздействии на вход функции
с использованием передаточной функции
цепи. Согласно выражению (13.6), при
воздействии на вход функции  ,
откликом функции будет переходная
функция
,
откликом функции будет переходная
функция  вида:
вида:
 .
.
С другой стороны,
известно, что изображение производной
функции по времени  ,
при
,
при  ,
равно произведению
,
равно произведению  .
.
Откуда  ,
,
или  ,
(13.10)
,
(13.10)
т.е. импульсная
характеристика
 цепи равна обратному преобразованию
Лапласа ее передаточной
цепи равна обратному преобразованию
Лапласа ее передаточной
 функции.
функции.
Пример. Найдем импульсную функцию цепи, схемы замещения которой представлены на рис. 13.12, а ; 13.13.
Решение
Переходная и передаточная функции этой цепи били получены ранее:

Тогда, согласно выражению (13.8)
где  .
.
|
|
График импульсной
характеристики  цепи представлен на рис. 13.15.
цепи представлен на рис. 13.15.
Выводы
Импульсная
характеристика  введена по тем же двум причинам, что и
переходная характеристика
введена по тем же двум причинам, что и
переходная характеристика  .
.
1. Единичное
импульсное воздействие  – скачкообразное и потому довольно
тяжелое для любой системы или цепи
внешнее воздействие. Следовательно,
важно знать реакцию системы или цепи
именно при таком воздействии, т.е.
импульсную характеристику
– скачкообразное и потому довольно
тяжелое для любой системы или цепи
внешнее воздействие. Следовательно,
важно знать реакцию системы или цепи
именно при таком воздействии, т.е.
импульсную характеристику  .
.
2. При помощи
некоторого видоизменения интеграла
Дюамеля можно, зная
 вычислить реакцию системы или цепи на
любое внешнее возмущение (см. далее пп.
13.4, 13.5).
вычислить реакцию системы или цепи на
любое внешнее возмущение (см. далее пп.
13.4, 13.5).
4. Интеграл наложения (дюамеля).
Пусть произвольный
пассивный двухполюсник (рис. 13.16, а
)
подключается к источнику непрерывно
изменяющегося с момента
 напряжения
напряжения (рис. 13.16,б
).
(рис. 13.16,б
).
|
|
Требуется найти
ток
 (или напряжение) в любой ветви двухполюсника
после замыкания ключа.
(или напряжение) в любой ветви двухполюсника
после замыкания ключа.
Задачу решим в два
этапа. Сначала искомую величину найдем
при включении двухполюсника на единичный
скачок напряжения, который задается
единичной ступенчатой функцией
 .
.
Известно, что
реакцией цепи на единичный скачок
является переходная
характеристика (функция)
 .
.
Например, для
 –
цепи переходная функция по току
–
цепи переходная функция по току (см. п.2.1), для
(см. п.2.1), для –
цепи переходная функция по напряжению
–
цепи переходная функция по напряжению .
.
На втором этапе
непрерывно изменяющееся напряжение
 заменим ступенчатой функцией с
элементарными прямоугольными скачками
заменим ступенчатой функцией с
элементарными прямоугольными скачками (см. рис. 13.16б
).
Тогда процесс изменения напряжения
можно представить как включение при
(см. рис. 13.16б
).
Тогда процесс изменения напряжения
можно представить как включение при
 постоянного напряжения
постоянного напряжения ,
а затем как включение элементарных
постоянных напряжений
,
а затем как включение элементарных
постоянных напряжений ,
смещенных относительно друг друга на
интервалы времени
,
смещенных относительно друг друга на
интервалы времени и имеющих знак плюс для возрастающей и
минус для падающей ветви заданной кривой
напряжения.
и имеющих знак плюс для возрастающей и
минус для падающей ветви заданной кривой
напряжения.
Составляющая
искомого тока в момент
 от постоянного напряжения
от постоянного напряжения равна:
равна:
 .
.
Составляющая
искомого тока от элементарного скачка
напряжения
 ,
включаемого в момент времени
,
включаемого в момент времени равна:
равна:
 .
.
Здесь аргументом
переходной функции является время
 ,
поскольку элементарный скачок напряжения
,
поскольку элементарный скачок напряжения начинает действовать на время
начинает действовать на время позднее замыкания ключа или, иначе
говоря, поскольку промежуток времени
между моментом
позднее замыкания ключа или, иначе
говоря, поскольку промежуток времени
между моментом начала действия этого скачка и моментом
времени
начала действия этого скачка и моментом
времени равен
равен .
.
Элементарный скачок напряжения
 ,
,
где
 – масштабный коэффициент.
– масштабный коэффициент.
Поэтому искомая составляющая тока
Элементарные
скачки напряжения включаются на интервале
времени от
 до момента
до момента ,
для которого определяется искомый ток.
Поэтому, суммируя составляющие тока от
всех скачков, переходя к пределу при
,
для которого определяется искомый ток.
Поэтому, суммируя составляющие тока от
всех скачков, переходя к пределу при ,
и учитывая составляющую тока от начального
скачка напряжения
,
и учитывая составляющую тока от начального
скачка напряжения ,
получаем:
,
получаем:
Последняя формула для определения тока при непрерывном изменении приложенного напряжения
 (13.11)
(13.11)
называется интегралом наложения (суперпозиции) или интегралом Дюамеля (первой формой записи этого интеграла).
Аналогично решается
задача при подключении цепи и источнику
тока. Согласно этому интегралу реакция
цепи, в общем виде,
 в некоторый момент
в некоторый момент после
начала воздействия
после
начала воздействия определяется всей той частью воздействия,
которая имела место до момента времени
определяется всей той частью воздействия,
которая имела место до момента времени .
.
Заменой переменных и интегрированием по частям можно получить другие формы записи интеграла Дюамеля, эквивалентные выражению (13.11):

Выбор формы записи
интеграла Дюамеля определяется удобством
расчета. Например, в случае, если
 выражается экспоненциальной функцией,
удобной оказывается формула (13.13) или
(13.14), что обуславливается простотой
дифференцирования экспоненциальной
функции.
выражается экспоненциальной функцией,
удобной оказывается формула (13.13) или
(13.14), что обуславливается простотой
дифференцирования экспоненциальной
функции.
При
 или
или удобно применять форму записи, в которой
слагаемое перед интегралом обращается
в нуль.
удобно применять форму записи, в которой
слагаемое перед интегралом обращается
в нуль.
Произвольное
воздействие
 может быть представлено также в виде
суммы последовательно включаемых
импульсов, как это изображено на рис.
13.17.
может быть представлено также в виде
суммы последовательно включаемых
импульсов, как это изображено на рис.
13.17.
|
|
При бесконечно
малой длительности импульсов
 получим формулы интеграла Дюамеля,
аналогичные (13.13) и (13.14).
получим формулы интеграла Дюамеля,
аналогичные (13.13) и (13.14).

Эти же формулы
можно получить из соотношений (13.13) и
(13.14), заменив а них производную функцию
 импульсной функцией
импульсной функцией .
.
Вывод.
Таким образом, на
основе формул интеграла Дюамеля (13.11) –
(13.16) и временных характеристик цепи
 и
и могут быть определены временные функции
откликов цепи
могут быть определены временные функции
откликов цепи на произвольные воздействия
на произвольные воздействия .
.
3. Импульсные характеристики электрических цепей
Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных условиях.
По определению ,
где – реакция цепи на импульсное воздействие;
– площадь импульса воздействия.
По известной импульсной характеристике цепи можно найти реакцию цепи на заданное воздействие: .
В качестве функции воздействия часто используется единичное импульсное воздействие называемое также дельта-функцией или функцией Дирака.
Дельта-функция – это функция всюду равная нулю, кроме , а площадь ее равна единице ():
 .
.
К понятию дельта-функция можно прийти, рассматривая предел прямоугольного импульса высотой и длительностью , когда (рис. 3):

Установим связь между передаточной функцией цепи и ее импульсной характеристикой, для чего используем операторный метод.
По определению:
Если воздействие (оригинал) рассматривать для наиболее общего случая в виде произведения площади импульса на дельта-функцию, т. е. в виде , то изображение этого воздействия согласно таблицы соответствий имеет вид:
 .
.
Тогда с другой стороны, отношение преобразованной по Лапласу реакции цепи к величине площади импульса воздействия, представляет собой операторную импульсную характеристику цепи:
 .
.
Следовательно, .
Для нахождения импульсной характеристики цепи необходимо применить обратное преобразование Лапласа:
![]() , т.
е. фактически
, т.
е. фактически
![]() .
.
Обобщая формулы, получим связь между операторной передаточной функцией цепи и операторными переходной и импульсной характеристиками цепи:
Таким образом, зная одну из характеристик цепи, можно определить любые другие.
Произведем тождественное преобразование равенства, прибавив к средней части .
Тогда будем иметь .
Поскольку
![]() представляет собой изображение
производной переходной характеристики,
то исходное равенство можно переписать
в виде:
представляет собой изображение
производной переходной характеристики,
то исходное равенство можно переписать
в виде:
Переходя в область оригиналов, получаем формулу, позволяющую определить импульсную характеристику цепи по известной ее переходной характеристике:
Если , то .
Обратное соотношение между указанными характеристиками имеет вид:
 .
.
По передаточной функции легко установить наличие в составе функции слагаемого .
Если степени числителя и знаменателя одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция является правильной дробью, то этого слагаемого не будет.
Пример: определить импульсные характеристики для напряжений и в последовательной -цепи, показанной на рисунке 4.

Определим :
По таблице соответствий перейдем к оригиналу:
 .
.
График этой функции показан на рисунке 5.
Рис. 5
Передаточная функция :
Согласно таблице соответствий имеем:
 .
.
График полученной функции показан на рисунке 6.

Укажем, что такие же выражения можно было получить с помощью соотношений, устанавливающих связь между и.
Импульсная характеристика по физическому смыслу отражает собой процесс свободных колебаний и по этой причине можно утверждать, что в реальных цепях всегда должно выполняться условие:
4. Интегралы свертки (наложения)
Рассмотрим порядок определения реакции линейной электрической цепи на сложное воздействие, если известна импульсная характеристика этой цепи . Будем считать, что воздействие представляет собой кусочно-непрерывную функцию , показанную на рисунке 7.

Пусть требуется найти значение реакции в некоторый момент времени . Решая эту задачу, представим воздействие в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени , показан на рисунке 7. Этот импульс характеризуется длительностью и высотой .
Из ранее рассмотренного материала известно, что реакцию цепи на короткий импульс можно считать равной произведению импульсной характеристики цепи на площадь импульсного воздействия. Следовательно, бесконечно малая составляющая реакции, обусловленная этим импульсным воздействием, в момент времени будет равной:
поскольку площадь импульса равна , а от момента его приложения до момента наблюдения проходит время .
Используя принцип наложения, полную реакцию цепи можно определить как сумму бесконечно большого числа бесконечно малых составляющих , вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени .
Таким образом:
 .
.
Эта формула верна для любых значений , поэтому обычно переменную обозначают просто . Тогда:
 .
.
Полученное соотношение называют интегралом свертки или интегралом наложения. Функцию, которая находится в результате вычисления интеграла свертки, называют сверткой и .
Можно найти другую форму интеграла свертки, если в полученном выражении для осуществить замену переменных:
 .
.
Пример: найти напряжение на емкости последовательной -цепи (рис. 8), если на входе действует экспоненциальный импульс вида:


 цепи
связан: с изменением энергетического состояния... (+0),. Uc(-0) = Uc(+0). 3. Переходная
характеристика
электрической
цепи
это: Отклик на единичное ступенчатое...
цепи
связан: с изменением энергетического состояния... (+0),. Uc(-0) = Uc(+0). 3. Переходная
характеристика
электрической
цепи
это: Отклик на единичное ступенчатое...
Исследование цепи второго порядка. Поиск входной и предаточной характеристики
Курсовая работа >> Коммуникации и связь3. Переходная и импульсная характеристики цепи Лаплас образ переходной характеристики имеет вид. Для получения переходной характеристики во... А., Золотницкий В. М., Чернышев Э. П. Основы теории электрических цепей .-СПб.:Лань, 2004. 2. Дьяконов В. П. MATLAB ...
Основные положения теории переходных процессов
Реферат >> ФизикаЛапласа; – временной, использующий переходные и импульсные характеристики ; – частотный, базирующийся на... классического метода анализа переходных колебаний в электрических цепях Переходные процессы в электрических цепях описываются уравнениями, ...
Академия России
Кафедра Физики
Лекция
Переходные и импульсные характеристики электрических цепей
Орел 2009
Учебные и воспитательные цели:
Разъяснить слушателям сущность переходной и импульсной характеристик электрических цепей, показать связь между характеристиками, обратить внимание на применение рассматриваемых характеристик для анализа и синтеза ЭЦ, нацелить на качественную подготовку к практическому занятию.
Распределение времени лекции
Вступительная часть……………………………………………………5 мин.
Учебные вопросы:
1. Переходные характеристики электрических цепей………………15 мин.
2. Интегралы Дюамеля………………………………………………...25 мин.
3. Импульсные характеристики электрических цепей. Связь между характеристиками………………………………………….………...25 мин.
4. Интегралы свертки………………………………………………….15 мин.
Заключение……………………………………………………………5 мин.
1. Переходные характеристики электрических цепей
Переходная характеристика цепи (как и импульсная) относится к временным характеристикам цепи, т. е. выражает некоторый переходный процесс при заранее установленных воздействиях и начальных условиях.
Для сравнения электрических цепей по их реакции к этим воздействиям, необходимо цепи поставить в одинаковые условия. Наиболее простыми и удобными являются нулевые начальные условия.
Переходной характеристикой цепи называют отношение реакции цепи на ступенчатое воздействие к величине этого воздействия при нулевых начальных условиях.
По определению ,
– реакция цепи на ступенчатое воздействие; – величина ступенчатого воздействия [В] или [А]. и делится на величину воздействия (это вещественное число), то фактически – реакция цепи на единичное ступенчатое воздействие.Если переходная характеристика цепи известна (или может быть вычислена), то из формулы можно найти реакцию этой цепи на ступенчатое воздействие при нулевых НУ
Установим связь между операторной передаточной функцией цепи, которая часто известна (или может быть найдена), и переходной характеристикой этой цепи. Для этого используем введенное понятие операторной передаточной функции:
Отношение преобразованной по Лапласу реакции цепи к величине воздействия
представляет собой операторную переходную характеристику цепи:Следовательно .
Отсюда находится операторная переходная характеристика цепи по операторной передаточной функции.
Для определения переходной характеристики цепи необходимо применить обратное преобразование Лапласа:
,воспользовавшись таблицей соответствий или (предварительно) теоремой разложения.
Пример: определить переходную характеристику для реакции напряжение на емкости в последовательной
-цепи (рис. 1):Здесь реакция на ступенчатое воздействие величиной
:откуда переходная характеристика:
Переходные характеристики наиболее часто встречающихся цепей найдены и даны в справочной литературе.
2. Интегралы Дюамеля
Переходную характеристику часто используют для нахождения реакции цепи на сложное воздействие. Установим эти соотношения.
Условимся, что воздействие
является непрерывной функцией и подводится к цепи в момент времени , а начальные условия – нулевые.Заданное воздействие
можно представить как сумму ступенчатого воздействия приложенного к цепи в момент и бесконечно большого числа бесконечно малых ступенчатых воздействий, непрерывно следующих друг за другом. Одно из таких элементарных воздействий, соответствующих моменту приложения показано на рисунке 2.Найдем значение реакции цепи в некоторый момент времени
.Ступенчатое воздействие с перепадом
к моменту времени обуславливает реакцию, равную произведению перепада на значение переходной характеристики цепи при , т. е. равную:Бесконечно малое же ступенчатое воздействие с перепадом
, обуславливает бесконечно малую реакцию , где есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция непрерывна, то:В соответствии с принципом наложения реакции
будет равна сумме реакций, обусловленных совокупностью воздействий, предшествующих моменту наблюдения , т. е.Обычно в последней формуле
заменяют просто на , поскольку найденная формула верна при любых значениях времени :Интеграл Дюамеля.
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую - как t.

Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.
В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .
В момент времени имеет место скачок напряжения ![]() , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .
, который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .
Полный ток в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.
Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя от суммы к интегралу, запишем
 . .
| (1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция по напряжению.
Последовательность расчета с использованием
интеграла Дюамеля
 В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: ![]() , , .
, , .
- Переходная проводимость
 .
.

18. Передаточная функция .
Отношение оператора воздействия к собственному оператору называют передаточной функцией или передаточной функцией в операторной форме.
 Звено, описываемое уравнением или уравнениями в символической или операторной форме записи можно охарактеризовать двумя передаточными функциями: передаточной функцией по входной величине u; и передаточной функцией по входной величине f.
Звено, описываемое уравнением или уравнениями в символической или операторной форме записи можно охарактеризовать двумя передаточными функциями: передаточной функцией по входной величине u; и передаточной функцией по входной величине f.
 и
и 
Используя передаточные функции, уравнение записывают в виде ![]() . Это уравнение представляет собой условную более компактную запись форму записи исходного уравнения.
. Это уравнение представляет собой условную более компактную запись форму записи исходного уравнения.
Наряду с передаточной функцией в операторной форме широко используют передаточную функцию в форме изображений Лапласа.
Передаточные функции в форме изображений Лапласа и операторной форме с точностью до обозначений совпадают. Передаточную функцию в форме, изображения Лапласа можно получить из передаточной функции в операторной форме, если в последней сделать подстановку p=s. В общем случае это следует из того, что дифференцированию оригинала - символическому умножению оригинала на p - при нулевых начальных условиях соответствует умножение изображения на комплексное число s.
Сходство между передаточными функциями в форме изображения Лапласа и в операторной форме чисто внешнее, и оно имеет место только в случае стационарных звеньев (систем), т.е. только при нулевых начальных условиях.
Рассмотрим простую RLC (последовательно) цепь, её передаточная функция W(p)=U ВЫХ /U ВХ

Интеграл Фурье.
Функция f
(x
),
определенная на всей числовой оси называется периодической
, если существует такое число, что при любом значении х
выполняется равенство ![]() . Число Т
называется периодом функции.
. Число Т
называется периодом функции.
Отметим некоторые с в о й с т в а этой функции:
1) Сумма, разность, произведение и частное периодических функций периода Т есть периодическая функция периода Т .
2) Если функция f (x ) период Т , то функция f (ax )имеет период .
3) Если f
(x
)- периодическая функция периода Т
, то равны любые два интеграла от этой функции, взятые по промежуткам длины Т
(при этом интеграл существует), т. е. при любых a
и b
справедливо равенство  .
.
Тригонометрический ряд. Ряд Фурье
Если f
(x
) разлагается на отрезке в равномерно сходящийся тригонометрический ряд:![]() (1)
(1)
То это разложение единственное и коэффициенты определяются по формулам:



где n =1,2, . . .
Тригонометрический ряд (1) рассмотренного вида с коэффициентами называется тригонометрическим рядом Фурье .
Комплексная форма ряда Фурье
Выражение называется комплексной формой ряда Фурье функции f (x ), если определяется равенством
 ,
где
,
где
Переход от ряда Фурье в комплексной форме к ряду в действительной форме и обратно осуществляется с помощью формул:
 (n
=1,2, . . .)
(n
=1,2, . . .)
Интегралом Фурье функции f(x) называется интеграл вида:
 , где
, где 
 .
.
Частотные функции.
Если подать на вход системы с передаточной функцией W(p) гармонический сигнал
то после завершения переходного процесса на выходе установится гармонические колебания
с той же частотой , но иными амплитудой и фазой, зависящими от частоты возмущающего воздействия. По ним можно судить о динамических свойствах системы. Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью исследования ее динамических свойств называется частотным анализом .
Подставим выражения для u(t) и y(t) в уравнение динамики
(aоp n + a 1 pn - 1 + a 2 p n - 2 + ... + a n)y = (bоp m + b 1 p m-1 + ... + b m)u.
Учтем, что
pnu = pnU m ejwt = U m (jw)nejwt = (jw)nu.
Аналогичные соотношения можно записать и для левой части уравнения. Получим:
По аналогии с передаточной функцией можно записать:
W(j ), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией . Легко заметить, что она может быть получена путем простой замены p на j в выражении W(p).
W(j ) есть комплексная функция, поэтому:
где P() - вещественная ЧХ (ВЧХ) ; Q() - мнимая ЧХ (МЧХ) ; А() - амплитудная ЧХ (АЧХ) : () - фазовая ЧХ (ФЧХ) . АЧХ дает отношение амплитуд выходного и входного сигналов, ФЧХ - сдвиг по фазе выходной величины относительно входной:
 ;
; ![]()

Если W(j ) изобразить вектором на комплексной плоскости, то при изменении от 0 до + его конец будет вычерчивать кривую, называемую годографом вектора W(j ), или амплитудно - фазовую частотную характеристику (АФЧХ) (рис.48).
Ветвь АФЧХ при изменении от - до 0 можно получить зеркальным отображением данной кривой относительно вещественной оси.
В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49): логарифмическая амплитудная ЧХ (ЛАЧХ) L() и логарифмическая фазовая ЧХ (ЛФЧХ) ().
Они получаются путем логарифмирования передаточной функции:

ЛАЧХ получают из первого слагаемого, которое из соображений масштабирования умножается на 20, и используют не натуральный логарифм, а десятичный, то есть L() = 20lgA(). Величина L() откладывается по оси ординат в децибелах .
Изменение уровня сигнала на 10 дб соответствует изменению его мощности в 10 раз. Так как мощность гармонического сигнала Р пропорциональна квадрату его амплитуды А, то изменению сигнала в 10 раз соответствует изменение его уровня на 20дб,так как
lg(P 2 /P 1) = lg(A 2 2 /A 1 2) = 20lg(A 2 /A 1).
По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой . Так как lg(0) = - , то ось ординат проводят произвольно.
ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси . Величина () откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: - + .
ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.
Обратные связи.
Принято считать, что звено охвачено обратной связью, если его выходной сигнал через какое-либо другое звено подается на вход. При этом, если сигнал обратной связи вычитается из входного воздействия (), то обратную связь называют отрицательной. Если сигнал обратной связи складывается с входным воздействием (), то обратную связь называют положительной.
Передаточная функция замкнутой цепи с отрицательной обратной связью - звена, охваченного отрицательной обратной связью,- равна передаточной функции прямой цепи , деленной на единицу плюс передаточная функция разомкнутой цепи

Передаточная функция замкнутой цепи с положительной обратной связью равна передаточной функции прямой цепи, деленной на единицу минус передаточная функция разомкнутой цепи
22. 23. Четырёхполюсники .
При анализе электрических цепей в задачах исследования взаимосвязи между переменными (токами, напряжениями, мощностями и т.п.) двух каких-то ветвей схемы широко используется теория четырехполюсников.
Четырехполюсник – это часть схемы произвольной конфигурации, имеющая две пары зажимов (отсюда и произошло его название), обычно называемые входными и выходными.
Примерами четырыхполюсника являются трансформатор, усилитель, потенциометр, линия электропередачи и другие электротехнические устройства, у которых можно выделить две пары полюсов.
В общем случае четырехполюсники можно разделить на активные, в структуру которых входят источники энергии, и пассивные, ветви которых не содержат источников энергии.
Для записи уравнений четырехполюсника выделим в произвольной схеме ветвь с единственным источником энергии и любую другую ветвь с некоторым сопротивлением (см. рис. 1,а).

В соответствии с принципом компенсации заменим исходное сопротивление источником с напряжением (см. рис. 1,б). Тогда на основании метода наложения для цепи на рис. 1,б можно записать
 Уравнения (3) и (4) представляют собой основные уравнения четырехполюсника; их также называют уравнениями четырехполюсника в А-форме (см. табл. 1). Вообще говоря, существует шесть форм записи уравнений пассивного четырехполюсника. Действительно, четырехполюсник характеризуется двумя напряжениями и и двумя токами и . Любые две величины можно выразить через остальные. Так как число сочетаний из четырех по два равно шести, то и возможно шесть форм записи уравнений пассивного четырехполюсника, которые приведены в табл. 1. Положительные направления токов для различных форм записи уравнений приведены на рис. 2. Отметим, что выбор той или иной формы уравнений определяется областью и типом решаемой задачи.
Уравнения (3) и (4) представляют собой основные уравнения четырехполюсника; их также называют уравнениями четырехполюсника в А-форме (см. табл. 1). Вообще говоря, существует шесть форм записи уравнений пассивного четырехполюсника. Действительно, четырехполюсник характеризуется двумя напряжениями и и двумя токами и . Любые две величины можно выразить через остальные. Так как число сочетаний из четырех по два равно шести, то и возможно шесть форм записи уравнений пассивного четырехполюсника, которые приведены в табл. 1. Положительные направления токов для различных форм записи уравнений приведены на рис. 2. Отметим, что выбор той или иной формы уравнений определяется областью и типом решаемой задачи.
Таблица 1. Формы записи уравнений пассивного четырехполюсника
| Форма | Уравнения | Связь с коэффициентами основных уравнений |
| А-форма | | |
| Y-форма | | ; ; ; ; |
| Z-форма | | ; ; ; ; |
| Н-форма | | ; ; ; ; |
| G-форма | | ; ; ; ; |
| B-форма | | ; ; ; . |
Характеристическое сопротивление и коэффициент
распространения симметричного четырехполюсника
В электросвязи широко используется режим работы симметричного четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.
 .
.
Это сопротивление обозначают как и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо
![]() ,
,
Академия России
Кафедра Физики
Лекция
Переходные и импульсные характеристики электрических цепей
Орел 2009
Учебные и воспитательные цели:
Разъяснить слушателям сущность переходной и импульсной характеристик электрических цепей, показать связь между характеристиками, обратить внимание на применение рассматриваемых характеристик для анализа и синтеза ЭЦ, нацелить на качественную подготовку к практическому занятию.
Распределение времени лекции
Вступительная часть……………………………………………………5 мин.
Учебные вопросы:
1. Переходные характеристики электрических цепей………………15 мин.
2. Интегралы Дюамеля………………………………………………...25 мин.
3. Импульсные характеристики электрических цепей. Связь между характеристиками………………………………………….………...25 мин.
4. Интегралы свертки………………………………………………….15 мин.
Заключение……………………………………………………………5 мин.
1. Переходные характеристики электрических цепей
Переходная характеристика цепи (как и импульсная) относится к временным характеристикам цепи, т. е. выражает некоторый переходный процесс при заранее установленных воздействиях и начальных условиях.
Для сравнения электрических цепей по их реакции к этим воздействиям, необходимо цепи поставить в одинаковые условия. Наиболее простыми и удобными являются нулевые начальные условия.
Переходной характеристикой цепи называют отношение реакции цепи на ступенчатое воздействие к величине этого воздействия при нулевых начальных условиях.
По определению ,
где – реакция цепи на ступенчатое воздействие;
– величина ступенчатого воздействия [В] или [А].
Так как и делится на величину воздействия (это вещественное число), то фактически – реакция цепи на единичное ступенчатое воздействие.
Если переходная характеристика цепи известна (или может быть вычислена), то из формулы можно найти реакцию этой цепи на ступенчатое воздействие при нулевых НУ
![]() .
.
Установим связь между операторной передаточной функцией цепи, которая часто известна (или может быть найдена), и переходной характеристикой этой цепи. Для этого используем введенное понятие операторной передаточной функции:
 .
.
Отношение преобразованной по Лапласу реакции цепи к величине воздействия представляет собой операторную переходную характеристику цепи:
Следовательно .
Отсюда находится операторная переходная характеристика цепи по операторной передаточной функции.
Для определения переходной характеристики цепи необходимо применить обратное преобразование Лапласа:
воспользовавшись таблицей соответствий или (предварительно) теоремой разложения.
Пример: определить переходную характеристику для реакции напряжение на емкости в последовательной -цепи (рис. 1):

Здесь реакция на ступенчатое воздействие величиной :
 ,
,
откуда переходная характеристика:
 .
.
Переходные характеристики наиболее часто встречающихся цепей найдены и даны в справочной литературе.
2. Интегралы Дюамеля
Переходную характеристику часто используют для нахождения реакции цепи на сложное воздействие. Установим эти соотношения.
Условимся, что воздействие является непрерывной функцией и подводится к цепи в момент времени , а начальные условия – нулевые.
Заданное воздействие можно представить как сумму ступенчатого воздействия приложенного к цепи в момент и бесконечно большого числа бесконечно малых ступенчатых воздействий, непрерывно следующих друг за другом. Одно из таких элементарных воздействий, соответствующих моменту приложения показано на рисунке 2.

Найдем значение реакции цепи в некоторый момент времени .
Ступенчатое воздействие с перепадом к моменту времени обуславливает реакцию, равную произведению перепада на значение переходной характеристики цепи при , т. е. равную:
Бесконечно малое же ступенчатое воздействие с перепадом , обуславливает бесконечно малую реакцию ![]() , где есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция непрерывна, то:
, где есть время, прошедшее от момента приложения воздействия до момента наблюдения. Так как по условию функция непрерывна, то:
В соответствии с принципом наложения реакции будет равна сумме реакций, обусловленных совокупностью воздействий, предшествующих моменту наблюдения , т. е.
 .
.
Обычно в последней формуле заменяют просто на , поскольку найденная формула верна при любых значениях времени :
 .
.
Или, после несложных преобразований:
 .
.
Любое из этих соотношений и решает задачу вычисления реакции линейной электрической цепи на заданное непрерывное воздействие по известной переходной характеристики цепи . Эти соотношения называют интегралами Дюамеля.
3. Импульсные характеристики электрических цепей
Импульсной характеристикой цепи называют отношение реакции цепи на импульсное воздействие к площади этого воздействия при нулевых начальных условиях.
По определению ,
где – реакция цепи на импульсное воздействие;
– площадь импульса воздействия.
По известной импульсной характеристике цепи можно найти реакцию цепи на заданное воздействие: ![]() .
.
В качестве функции воздействия часто используется единичное импульсное воздействие называемое также дельта-функцией или функцией Дирака.
Дельта-функция – это функция всюду равная нулю, кроме , а площадь ее равна единице ():
 .
.
К понятию дельта-функция можно прийти, рассматривая предел прямоугольного импульса высотой и длительностью , когда (рис. 3):

Установим связь между передаточной функцией цепи и ее импульсной характеристикой, для чего используем операторный метод.
По определению:
 .
.
Если воздействие (оригинал) рассматривать для наиболее общего случая в виде произведения площади импульса на дельта-функцию, т. е. в виде , то изображение этого воздействия согласно таблицы соответствий имеет вид:
 .
.
Тогда с другой стороны, отношение преобразованной по Лапласу реакции цепи к величине площади импульса воздействия, представляет собой операторную импульсную характеристику цепи:
 .
.
Следовательно, .
Для нахождения импульсной характеристики цепи необходимо применить обратное преобразование Лапласа:
Т. е. фактически .
Обобщая формулы, получим связь между операторной передаточной функцией цепи и операторными переходной и импульсной характеристиками цепи:
Таким образом, зная одну из характеристик цепи, можно определить любые другие.
Произведем тождественное преобразование равенства, прибавив к средней части .
Тогда будем иметь .
Поскольку представляет собой изображение производной переходной характеристики, то исходное равенство можно переписать в виде:
Переходя в область оригиналов, получаем формулу, позволяющую определить импульсную характеристику цепи по известной ее переходной характеристике:
Если , то .
Обратное соотношение между указанными характеристиками имеет вид:
 .
.
По передаточной функции легко установить наличие в составе функции слагаемого .
Если степени числителя и знаменателя одинаковы, то рассматриваемое слагаемое будет присутствовать. Если же функция является правильной дробью, то этого слагаемого не будет.
Пример: определить импульсные характеристики для напряжений и в последовательной -цепи, показанной на рисунке 4.

Определим :
По таблице соответствий перейдем к оригиналу:
 .
.
График этой функции показан на рисунке 5.
Рис. 5
Передаточная функция :
Согласно таблице соответствий имеем:
 .
.
График полученной функции показан на рисунке 6.

Укажем, что такие же выражения можно было получить с помощью соотношений, устанавливающих связь между и .
Импульсная характеристика по физическому смыслу отражает собой процесс свободных колебаний и по этой причине можно утверждать, что в реальных цепях всегда должно выполняться условие:
4. Интегралы свертки (наложения)
Рассмотрим порядок определения реакции линейной электрической цепи на сложное воздействие, если известна импульсная характеристика этой цепи . Будем считать, что воздействие представляет собой кусочно-непрерывную функцию , показанную на рисунке 7.

Пусть требуется найти значение реакции в некоторый момент времени . Решая эту задачу, представим воздействие в виде суммы прямоугольных импульсов бесконечно малой длительности, один из которых, соответствующий моменту времени , показан на рисунке 7. Этот импульс характеризуется длительностью и высотой .
Из ранее рассмотренного материала известно, что реакцию цепи на короткий импульс можно считать равной произведению импульсной характеристики цепи на площадь импульсного воздействия. Следовательно, бесконечно малая составляющая реакции, обусловленная этим импульсным воздействием, в момент времени будет равной:
поскольку площадь импульса равна , а от момента его приложения до момента наблюдения проходит время .
Используя принцип наложения, полную реакцию цепи можно определить как сумму бесконечно большого числа бесконечно малых составляющих , вызванных последовательностью бесконечно малых по площади импульсных воздействий, предшествующих моменту времени .
Таким образом:
 .
.
Эта формула верна для любых значений , поэтому обычно переменную обозначают просто . Тогда:
 .
.
Полученное соотношение называют интегралом свертки или интегралом наложения. Функцию , которая находится в результате вычисления интеграла свертки, называют сверткой и .
Можно найти другую форму интеграла свертки, если в полученном выражении для осуществить замену переменных:
 .
.
Пример: найти напряжение на емкости последовательной -цепи (рис. 8), если на входе действует экспоненциальный импульс вида:



Воспользуемся интегралом свертки:
 .
.
Выражение для ![]() было получено ранее.
было получено ранее.
Следовательно, ![]() , и
, и  .
.

Такой же результат можно получить, применив интеграл Дюамеля.
Литература:
Белецкий А. Ф. Теория линейных электрических цепей. – М.: Радио и связь, 1986. (Учебник)
Бакалов В. П. и др. Теория электрических цепей. – М.: Радио и связь, 1998. (Учебник);
Качанов Н. С. и др. Линейные радиотехнические устройства. М.: Воен. издат., 1974. (Учебник);
Попов В. П. Основы теории цепей – М.: Высшая школа, 2000.(Учебник)






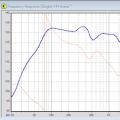 Как из свенов сделать то, что хотя бы можно слушать
Как из свенов сделать то, что хотя бы можно слушать Samsung Galaxy S5: Советы и рекомендации Samsung galaxy s5 первое включение
Samsung Galaxy S5: Советы и рекомендации Samsung galaxy s5 первое включение Baidu Root (русская версия) Baidu root рут не получен
Baidu Root (русская версия) Baidu root рут не получен